Devin Pope writes:
I wanted to send you an updated version of Jonah Berger and my basketball paper that shows that teams that are losing at halftime win more often than expected.
This new version is much improved. It has 15x more data than the earlier version (thanks to blog readers) and analyzes both NBA and NCAA data.
Also, you will notice if you glance through the paper that it has benefited quite a bit from your earlier critiques. Our empirical approach is very similar to the suggestions that you made.
See here and here for my discussion of the earlier version of Berger and Pope’s article.
Here’s the key graph from the previous version:
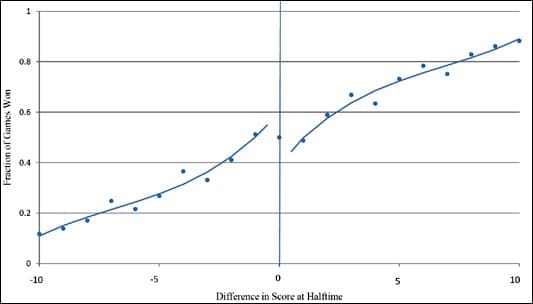
And here’s the update:
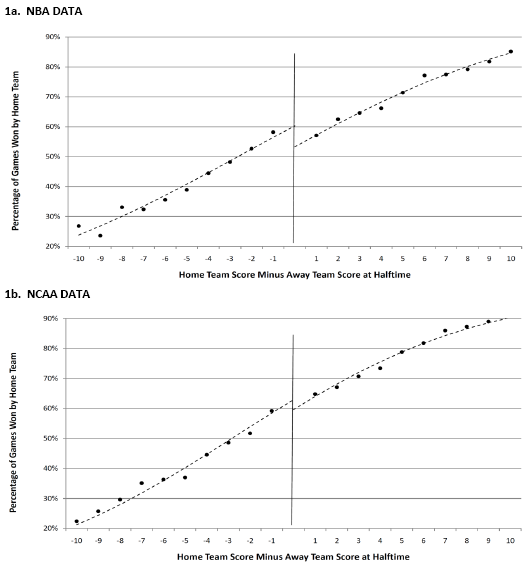
Much better–they got rid of that wacky fifth-degree polynomial that made the lines diverge in the graph from the previous version of the paper.
What do we see from the new graphs?
– In the NBA, it’s no better to be ahead by a point than down by a point at halftime. In the NCAA, it appears to be better to be ahead.
– In either league, being ahead by one more point at halftime increases your change of winning by about 4 percentage points.
The abstract is clear:
Analysis of over 45,000 collegiate and 18,000 professional basketball games illustrates that being slightly behind at halftime leads to a discontinuous increase in winning percentage. Teams that are losing by a small amount win approximately 2 (NCAA) and 6 (NBA) percentage points more often than expected.
“More often than expected” is a good way to put it. Compared the previous draft, the estimate for the NCAA has declined from 6.6 percentage points to a more plausible 2 percentage points. The authors also do some supplementary analyses to rule out some other possible explanations.
It’s the online peer review system in action.
I just have one question: Why do the two graphs from the recent paper not include the data point at 0? This would supply some information, no?
>> I just have one question: Why do the two graphs from the recent paper not include the data point at 0?
My question: Why is there a discontinuity imposed?
I agree, the discontinuity is imposed, not inferrable from the data.
Replacing the point at zero, and refitting would be more convincing. I think the blip in the residual at -1 would still be there, but it would depend on where the zero data point is, and what kind of model you use for the trend (ie. polynomial, or loess or whatever).
The most interesting thing I see from these graphs is that home teams have about a 3 point advantage in both leagues. Is this because of 'home team advantage' or is there something that causes better teams to play more home games. I'm fairly ignorant of how basketball games are scheduled.
I don't really understand what you mean when you say the discontinuity's imposed. They fit the model:
Win = a + b(losing at halftime dummy) + d(score difference at halftime) + controls + error
and test b – the additional chance of winning given you're losing at halftime. There's no reason the discontinuity has to exist, b could well have turned out to be zero, or close to it; or negative, rather than 2% or 6%, and they wouldn't have got a result. The discontinuity's allowed for, but it certainly doesn't have to be there.
To expand on Alex's point, testing for b > 0 vs. b
john/alex: so the fitted line should (on the left) stop at x=-1, and then a different line should start from x=0 on the rest of the plot.
For a really empirical approach, why not simply give percent home wins for e.g. x=-1, 0, 1? (with some measure of uncertainty, of course) There are thousands of data points here, I'm not sure the logistic-linear modeling effort adds a lot over what this would tell you.
If you put a dummy on "losing at halftime" you WILL get SOME non-zero value for that coefficient. It may be non-statistically-significant, but it will be there. Hence, your model will have a discontinuity. If the coefficient is small, the discontinuity is small… But it is always a discontinuity. It doesn't seem obvious that the right model is a discontinuous one.
A better analysis would be to ask: is the local effect in the vicinity of 0 different from the effect away from zero. A loess type fit vs a linear fit would give a better comparison of the hypothesis that there is something nonlinear going on near zero.
Another way to do it would be to compare a linear fit with weighted averages of the points around zero for different weighting schemes. For example a weighting scheme that is bell shaped with scale -3 to +3 vs a weighted scheme with a bell shaped weight with scale -8 to +8. Are the estimated lines different, and in what way?
daniel: there is no right model.
For the job of assessing the difference in win rate for teams who are behind versus being ahead, taking into account the degree behind or ahead (and the other things they adjust for) the Pope-Berger model/analysis seems okay. One could quibble with the assumed linearity (or the cubic version they also try) and the independence of data points, but it's not a crazy approach.
I don't think linearity is in itself of interest here; they're just using regression (and its 'b' coefficient) to make a particular comparison, between two groups of games.
"I just have one question: Why do the two graphs from the recent paper not include the data point at 0? This would supply some information, no?"
No. For every team that wins a game when tied at halftime, the other team loses a game when tied at halftime, so the point would be at 50%.
Steve: If you do it based on the home team (which makes sense, I think), then the point at zero does contain information.