Brent Goldfarb and Andrew King, in a paper to appear in the journal Strategic Management, write:
In a recent issue of this journal, Bettis (2012) reports a conversation with a graduate student who forthrightly announced that he had been trained by faculty to “search for asterisks”. The student explained that he sifted through large databases for statistically significant results and “[w]hen such models were found, he helped his mentors propose theories and hypotheses on the basis of which the ‘asterisks’ might be explained” (p. 109). Such an approach, Bettis notes, is an excellent way to find seemingly meaningful patterns in random data. He expresses concern that these practices are common, but notes that unfortunately “we simply do not have any baseline data on how big or small are the problems” (Bettis, 2012: p. 112).
In this article, we [Goldfarb and King] address the need for empirical evidence . . . in research on strategic management. . . .
Bettis (2012) reports that computer power now allows researchers to sift repeatedly through data in search of patterns. Such specification searches can greatly increase the probability of finding an apparently meaningful relationship in random data. . . . just by trying four functional forms for X, a researcher can increase the chance of a false positive from one in twenty to about one in six. . . .
Simmons et. al (2011) contend that some authors also push almost significant results over thresholds by removing or gathering more data, by dropping experimental conditions, by adding covariates to specified models, and so on.
And, beyond this, there’s the garden of forking paths: even if a researcher performs only one analysis of a given dataset, the multiplicity of choices involved in data coding and analysis are such that we can typically assume that different comparisons would have been studied had the data been different. That is, you can have misleading p-values without any cheating or “fishing” or “hacking” going on.
Goldfarb and King continue:
When evidence is uncertain, a single example is often considered representative of the whole (Tversky & Kahneman, 1973). Such inference is incorrect, however, if selection occurs on significant results. In fact, if “significant” results are more likely to be published, coefficient estimates will inflate the true magnitude of the studied effect — particularly if a low powered test has been used (Stanley, 2005).
They conducted a study of “estimates reported in 300 published articles in a random stratified sample from five top outlets for research on strategic management . . . [and] 60 additional proposals submitted to three prestigious strategy conferences.”
And here’s what they find:
We estimate that between 24% and 40% of published findings based on “statistically significant” (i.e. p<0.05) coefficients could not be distinguished from the Null if the tests were repeated once. Our best guess is that for about 70% of non-confirmed results, the coefficient should be interpreted to be zero. For the remaining 30%, the true B is not zero, but insufficient test power prevents an immediate replication of a significant finding. We also calculate that the magnitude of coefficient estimates of most true effects are inflated by 13%.
I’m surprised their estimated exaggeration factor is only 13%; I’d have expected much higher, even if only conditioning on “true” effects (however that is defined).
I have not tried to follow the details of the authors’ data collection and analysis process and thus can neither criticize nor endorse their specific findings. But I’m sympathetic to their general goals and perspective.
As a commenter wrote in an earlier discussion, it is the combination of a strawman with the concept of “statistical significance” (ie the filtering step) that seems to be a problem, not the p-value per se.
Gonna hijack this post for a second. I frequent this blog daily and some of it is just way over my head. That being said, does anyone recommend any simple yet complete reference materials on Bayesian vs Frequentist statistcs? I’ve only done hypothesis testing in my studies so far. One of the 3 things I want to do in my life is to get a PhD in Statistics. I still have 2 more years of college left so I still have some time! I was hoping to get a jump start in the field. I’m (slowly) learning R as well. Any help would be much appreciated :)
If you’re in college, why don’t you take some statistics courses?
Rasmus Baath’s research blog has some Bayesian alternatives to frequentist’s tests/analyses: “Bayesian First Aid” (http://www.sumsar.net/).
Here’s one about an alternative to the paired t-test: http://www.sumsar.net/blog/2014/02/bayesian-first-aid-one-sample-t-test/
If you are game, this animation depicts Bayesian inference in a simple one unknown parameter and sample size up to 5.
https://galtonbayesianmachine.shinyapps.io/GaltonBayesianMachine/
It can be extended up to 7 or more parameters and large sample sizes if the likelihood is available. Its just an inefficient way to sample from a posterior. With another layer of simulation you can get frequency properties (to a reasonable level of approximation) and hence compare of Frequency view to a Bayesian view.
But one needs to up to game a try to think it through.
(Maybe also read the paper by Stiger.)
Fridays – link to Stigler’s paper http://onlinelibrary.wiley.com/doi/10.1111/j.1467-985X.2010.00643.x/abstract
Keith, thanks for the links to the demo & to Stigler’s paper, both very interesting.
There are very few web links to the demo page. Did you create this yourself? If so, it’s pretty cool, thanks for your time & effort. If you feel like doing any further work on it: IMHO the explanatory text at present is pretty terse and not completely obvious. A link to the Stigler paper or other another reference would be appropriate as well, I think. Also, there’s a typo : to vs. too. I’m sure any improvements along these lines would be appreciated by beginning students. Thank you in advance for any consideration, assuming you’re the author.
Brad: Thanks, I used Shiny from RStudio which really made things easy – almost.
What happens is I underestimate the work required,don’t quite get finished, have to put things on hold but do decide to share the preliminary work (which wears on some folks patience.)
The animations have become the dog wagging the tail in an approach to use two stage sampling/simulation to transparently implement Bayesian inference and then Frequentist inference with simulation based repeated sampling. I have given a couple webinars using that and a recent talk at Carleton University – but its work stalled in process. There are no teaching opportunities nearby at present for me and I believe it really needs to be fully worked into a course.
There is a feature/bug currently in Shiny in that when I redo simulations and save in the same file names as initially used, Shiny dose not display the new simulations as it _knows_ its already shown those files (there was a discussion about this on stack exchange.)
Andrew will likely be kind enough to share my email address with you if you would like to discuss this further.
Also, I have put your suggestions on a to do list, thanks.
Brad: Addressed some of you considerations here https://phaneron0.wordpress.com/2012/11/23/two-stage-quincunx-2/
But then noticed this on my Shiny account “Account is suspended until Jun 10, 2015 10:37:29 AM due to “exceeded usage hours”.
All of your applications will be unavailable until then, or you can upgrade your account.”
I’ll contact the RStudio guys to try and find a way to allow more viewing without having to pay (again – I underestimate the work required.)
Matthew,
For the past several years, I’ve been offering a short course on “Common Mistakes in Using Statistics”. It doesn’t explicitly do “Frequentist vs Bayesian,” but points out a lot of the problems with frequentist statistics. It’s intended to be accessible to people who have had only an introductory course in (frequentist) statistics. You can find this year’s course page (still a few things that will be added over the weekend) at the link from my name above.
I can imagine fishing, p hacking etc. but I never understand the “different comparisons would have been studied had the data been different” argument.
Can someone explain that more.
I thought Prof Gelman’s critique of the women-wear-red-when-ovulating study covered this very clearly. Is pink a shade of red, or its own color? Hot pink, pale pink, mauve? Just red tops, or red anywhere? Is a white dress with red trim coded white or red? What do we guess about ovulation dates? Etc.
Kyle,
Indeed, it’s even worse than that, in that they did a follow-up study in which the data looked different, and they did a different analysis. So their own practice demonstrated the garden of forking paths. Again, I think it’s ok to do different analyses with different data, I just don’t think it’s ok to try to claim much from a p-value that doesn’t recognize this multiplicity.
@Kyle:
Thanks. So, in that case pre-registration ought to be a full & complete defense against forking-paths. Is it?
I seem to think Andrew say, it is not (I may be wrong). That is the part that confuses me.
i.e. If a researcher pre-registers a study, and lays out in great, painstaking detail his methods do we still have the garden of forking paths?
No it’s not a defense. As solutions go, preregistration is about like observing that blind car drivers crash a lot while in 5th gear and then solving this problem by requiring blind people to only drive in reverse.
The idea that the moment in time when the researcher thought to do the calculation changes it’s validity even when every other fact, number, and reality is unchanged is blatantly absurd. If Frequentist philosophy leads people to think that, then frequentism is blatantly absurd. The practical problem here is that Gelman and others are identify an absurd cause for the problem, so naturally they produce ridiculous solutions to the problem.
Here’s the reality. If you’re data has physical constraints which force a regularity in the data, such as for example sunspot data, you can commit all kinds of “garden of forked path”, “hacking”, “fishing” sins and still get a decent model.
If you’re data has no such constrains, as for example in stock market data, then even with pristinly perfect p-values you’ll still get models which blow up in your face, a fact which is well known to many a broke quantitative trader.
Frequentism fools people into thinking their model verification steps tell them whether their data is like the former case or the later. This isn’t true. So statisticans keep producing frequentist inspired analysis which seems to be well test and validated, but which Mother Nature rather stubbornly refuses to reproduce. Indeed there is no function of the data like p-values which could settle the issue since the same data numbers can result from an infinite variety of causes, some stable, some not.
There is a subtly here though. In order to preregister an analysis you have to understand the physical reality better than you do if you create the models after having seen the data. Because of that, there will be a tendency for preregistered analysis to deal with a data that is more like sunspot data. For that reason there may be a correlation between preregistration and better study results.
This correlation isn’t causation though. Once you’ve correctly identified the problem, you can dispense with preregistration entirely. Remember that preregistration isn’t harmless. It necessarily limits what the analyst can do with the data and necessarily throws some of the information in the data away.
Why do you dismiss this correlation between pre-registration and better quality results as mere non-causal correlation?
Doesn’t predictive power convince you more than post hoc rationalization?
Rahul:
It’s like this. A p-value is literally a statement about what would’ve happened, had the data been different. It’s a statement about the probability distribution of the test statistic, T(y), with the probability coming from the random distribution of y as determined by the experiment (in statistics jargon, the “sampling distribution,” p(y|theta)).
John Carlin and I discuss this in our recent paper.
To have a p-value at all, you need to define T(y) for all possible values of y; that is, you need to make an assumption about what you would’ve done, had the data been different. Preregistration is one way to ensure this assumption is correct. In the studies we have been discussing (ESP, ovulation and voting, clothing color, cancer recurrence, beauty and sex ratios, embodied cognition, etc etc etc), there is no reason to believe that T(y) was ever determined as a general function of the data y. Rather, y was observed and then T(y) was chosen. This is the garden of forking paths.
As I’ve also emphasized, I don’t think it’s necessary for studies to be pre-registered. In general, I don’t see p-values as a particularly useful data summary and I certainly don’t think they’re generally a good guide to practice, nor do I at all support the common practice of taking “p less than 0.05” as a synonym for “true.” But, if a researcher is going to lean on a p-value, then, yes, I think it makes sense to examine the assumptions that go into it, in particular the (generally false) assumption that the particular data analysis that was chosen for the particular data at hand, would’ve been performed had the data been different.
So the “meaningful”-ness of a p-value can change radically depending on what time the researcher mentally picked T(y) even though the data, assumptions, and physical reality hasn’t changed at all? Hell, you’re even using the exact same T(y)! Simply the date the research thought of it changes everything!
If that’s a legitimate interpretation of p-values according to frequentist intuition, then that just proves Frequentism is an insane pile of steaming horse manure and should be dropped immediately.
Here’s a crazy idea I’ve been thinking on lately: evidence drawn from data + physical assumptions only depends on the data and the assumptions and isn’t affect by the date-time stamp of my thoughts. Any statistical method that doesn’t have that property is indistinguishable from reading the entrails of chickens to predict the future.
Anon:
No, the point is that “T(y)” is not clearly defined. I think your chicken-entrails statement is too strong—I do think that a p-value coming from a preregistered study provides some information—but, in general, the point is that people should be clear on the assumptions underlying their inferential statements. And I think that many users of p-values honestly don’t realize that their inferential statements depend crucially on what they would’ve done, had the data been different. In that way, it’s no different than the famous Monty Hall problem.
Either p-values provide the same information no matter what date-time stamp someone thought to compute it, or they’re bogus.
Anon:
It’s not about the time, it’s about what would’ve been done had the data been different. I agree that p-values typically don’t mean what people want them to mean, but I don’t think they’re “bogus”; they’re just not all that they’re advertised as being.
Andrew,
You said “a p-value coming from a preregistered study provides some information”. The only physical difference between this and a p-value calculated after the fact is the time the person decided to calculate it. Speculations about what would happen in a parallel universe where the data were different are unproven and unprovable tripe.
There’s no getting around this. If your understanding of statistics leads you to believe the information content of a p-value changes by when the researcher decided to calculate it, even though all the numbers, assumptions, and physical reality remains unchained, then there are very deep and serious problems with your understanding of statistics. Those problems will manifest themselves in widespread and systematic failures of p-values as tool for science, which it should be noted, is exactly what’s happened.
Here’s where you reasoning is going astray. You observe:
(A) P-values are crap in practice.
(B) I have a theory which says the problem arises because if the data had been different (i.e. if we lived in a universe different than the current one) then the researcher would have behaved differently.
So you say “B implies A” and “A” is true therefore your crazy theory B is correct. But that’s a false conclusion. You actually don’t have a shred of evidence that B is true. There are a whole world of reasons A cold be true, none of which involve details about alternate universes. One of them is that p-values and the philosophy that lead to it are straight up bogus.
Fellow Anon,
If you use a “no difference” null hypothesis and know p-value + sample size you know the effect size (in units of sd). That is all the p-value tells you in that case. It is just as valid as an effect size. The failure to recognize this and compensatory attempts to usefully interpret it as a probability have lead to great confusion.
Anoneuoid,
Since a p-value is a function of the data it must contain some information that’s in the data. If that information happens to be important then in that sense it is useful (given enough functions of the data you could reconstruct the data). In that mathematical sense, no non-trivial function of the data can be said to be strictly useless.
However, if a correct application of p-values involves a frequentist understanding and that frequentist philosophy implies the data-time stamp of the moment when the researcher decided to compute the p-value significantly affects the evidential import of the p-value even though not a single number, fact, or assumption has changed, then frequentist philosophy is completely bogus and p-values are useless for frequentist purposes.
What if you have two researchers and they decide to compute the p-values at radically different times? One well before the experiment and one after the data is seen?
Gelman’s intuition tells him that if we’d do things differently in a different universe that yielded did data then that reduces the meaningfulness of the p-value. Since we’re just making up facts about alternative universes here let me boldly speculate that in a different universe we would all be tree frogs and our statistical analysis would consist of eating flies.
There. I’ve just established that all p-values are meaningless by Gelman’s own reasoning.
p-values come from the sampling theory, which more or less says that the universe might state the same, but that the data could be different. Your beef is not with p-values, but with the concept of probability.
The issue is that if the sampling distribution isn’t specified beforehand, it can be subtly tailored to suit the data in a way that violates the assumptions of the test.
p-values depend not just on the data, but on the model assumptions used to analyze the data. In a pre-registered study, presumably the model assumptions used to analyze the data are specified before collecting the data, whereas in a not-preregistered study, the researcher may use the data to decide what model assumptions to use.
Also, the pre-registered study presumably specifies how the data will be gathered, whereas a non-preregistered study might change data-collection method in mid-stream. Thus the data might not be the same for the preregistered and the non-preregistered studies.
And even the same method of data collection could get different data at different times.
I am not trying to protect p-values. I think, my point of view is close to that of Prof. Gelman. p-values are useful to control for simple possibility that there is not enough data to say something interesting. Other than that, your assumptions, model, conclusions etc. has to stand on their own and cannot be assumed to be true simply because you have performed some test.
> It’s a statement about the probability distribution of the test statistic, T(y), with the probability coming from the random distribution of y as determined by the experiment (in statistics jargon, the “sampling distribution,” p(y|theta)).
One thing that’s always bothered me about p-values* is that they only tell one side of the story. What does T(y) look like for ~theta. Let’s say I have data from which I can reasonably infer T(y|H_0). How can you make a claim of significance if you don’t know T(y|H_i) and p(H_i) for plausible hypotheses, H_i? In principle, one could observe apparently anomalous T(y) values with respect to H0 only to find that they’re even more anomalous with respect to {H_i}. If that were the case, could you claim significance on the basis of p-value? I’m going with “No.”
*I say this never having taken a statistics course so perhaps I’m missing something basic.
Chris:
It is what it is. There’s no H_0 and H_i, there’s just a model. What you want, to compare models, it’s fine, but it’s something different, p-values won’t do this, there are other tools for this purpose.
Okay, no H_0 and H_i, just a model. Let’s say I fit a model to my data and obtain a set of parameter values with an associated parameter covariance matrix. Or I do a bootstrap analysis and generate a pdf for parameter values. Either way, I’d say that it’s the characteristics of the pdf (inferred or generated) that are interesting, i.e., What’s the mean or maybe the mode of the distribution? What’s the variance? Are the tails heavy? I don’t have a particular point there, just that if I was handed the results of study I don’t think that reported p-values would be of greatest interest to me. I’d want to know the size of the effect the authors were investigating and the associated uncertainty. Whether or not the estimated effect is significant given the estimated uncertainty is a judgment call.
Some background: In my work decisions are almost all of the of the H_j or ~H_j variety (where j=1-many). H_0 is one ~H_j option but there may be many others. Towards that end it’s p(H_j|data) and p(data|H_j)/max{p(data|~H_j} that are of interest. You want to know p(data|H_j) but it’s not an end in and of itself.
Chris:
I think p-values have their purpose but I agree, I use them very rarely in my applied work.
I like this calculation: “p(data|H_j)/max{p(data|~H_j}”. It makes it obvious that we should be comparing multiple hypotheses rather than only a “null” and one vaguely derived from our favorite theory. Is there a name for it?
Sure. That’s pretty closely related to a likelihood ratio statistic.
JD,
I believe I misread that notation but it still yielded something interesting. I was thinking it meant there are n hypotheses and we calculate the likelihood under each of them. Then we normalize to highest likelihood. If you do that it looks silly to only compare null vs not null, the possible explanations have only been weakly investigated. I don’t think I’ve seen this done but maybe I have confused myself. To be clear I am not thinking that each possible parameter value counts as a different hypothesis.
Also, thinking about it more we would want to correct for the number of parameters so I suppose the various approaches to calculating an information criterion are doing this.
@JD: It would be fair to describe me as a Likelihoodist – http://www.stat.ufl.edu/archived/casella/Talks/BayesRefresher.pdf (See chart #2 and #3)
@Anoneuoid: I used bastard notation. Sorry for that.
With respect to my H_j hypotheses, figure each is a different linear subspace model for a k-dimensional measurement vector. When I’ve got n hypotheses where I don’t know p(H_j) then I make my decision based on the maximum likelihood ratio, conditional on cost(fit residuals) threshold then I figure that my H_j hypotheses didn’t include the actual cause of the observation. Alternatively stated: If none of my models fit the data well then I don’t presume that the best fit is the right explanation. If I thought (or when I think) that I have a handle on p(H_j) then I’d calculate p(data|H_j) but when I don’t then making decisions based on likelihood ratio seems to produce better results – better results in the sense of keeping the overall risk (loss) low.
Chris G: that was a great set of slides from Casella. His definition of 90% CIs is the clearest I have seen so far: In repeated sampling, 90% of realized intervals cover the true parameter.
Chris, Yes, the classical testin theory has been extended to the case were there is a partition of the probability distributions space in several subsets, and tests are used to assign the unknown distribution to one of these abstract models. Russian theoretical textbooks often treat this in great detail.
Rahul,
You can have some fun with this Garden of Forked paths stuff. Suppose you’re doing an experiment to measure the gravitational constant. With gravity being what it is we’d compute a given p-value to test whether it differs from some accepted value.
However, what if the gravitation constant was so strong that all matter would shrink to a point and humans never would have existed? Then clearly our data and analysis wouldn’t be the same.
Therefore according the Garden of Forked Paths, the p-value we calculated for the gravitational constant is meaningless.
Anon:
No, the distribution used in the p-value averages over all possible data, conditional on the parameters. In your note, you are averaging over all possible parameter values. That is different.
Anyway, as I never tire of saying, I’m not such a fan of p-values. I’m just saying that if you want to summarize inference by p-values, then you need to define what your test statistic would be, for data that you haven’t seen.
If you have pre-defined your test statistic, & every other aspect of the data analysis, then why do we still have the garden?
Rahul:
There is no garden of forking paths if all is preregistered.
Thank you. That cleared away a lot of my confusion.
In which case, why not take a very strong stand about pre-registration? At least for studies that do not advertise themselves as merely exploratory.
Why does it seem to me that in practice academics & journal editors are loathe to require pre-registration? Even you in your work, hardly ever pre-register, right?
But if you are not going to insist that your beautiful p<0.05 statistics proves whatever claim you are making irrespectful of how flimsy your assumptions are, how improbable the magnitude of the effect is etc., etc. why would anybody bother? There is no sin to peek at your data before inventing a hypothesis and analysis if you have more basis for them rather than, you know.
@DO
Maybe the claim did not have p values at all? The utility of pre-registration still remains.
I would like to know whether you formulated your standards of evidence before looking at the data or after. So long as you will claim *something*, you will need an argument to justify that claim.
And pre-registration lets me know whether you had that argument before you saw the data. Or whether you developed a post hoc rationalization after you saw the data. A just so story.
Essentially, pre-registration lets me test the predictive power of your hypothesis on data other than the one on which you developed the particular hypothesis.
Here’s an idea you could do. Gather together all the external factors which imply “meaningful” p-values. Don’t just use the date-time when the researcher decided to use that statistic, include everything else as well.
For example, study which researcher’s genetic markers which are correlated with “meaningful” p-values. What about how much coffee the researcher drank that day? What about whether researcher is male or female? Or their religious affiliation? If frequentist understanding of probabilities demands that the psychological state of researcher affects the meaningfulness of the p-vlues, then frequentists might all well go all-in on the idea.
Collect all these external factors together and use them create a giant regression model which predicts when p-values are “meaningful”. That should solve all the problems with the statistical sciences. I’m sure the first idiot that does this will get a nobel prize or something.
I’m not averaging over anything. I keep saying “if the garden of forked paths makes sense to frequentists then frequentism is insane”. You keep repeating effectively that “the garden of forked paths does makes sense to frequentists”.
I’m not disagreeing with you.
Put it this way. Take a T(y), distribution P(y), and some data y* and compute a p-value with these. Let’s agree that that this p-value number means something without getting bogged down on what that meaning is. It may not mean what people think it does, and it may not be very useful, but it is a function of the data y* and so in a sense carries some of the information that is implicit in the data. It has some correct true meaning. The same goes for any other function of y*.
What I claim is that the “true” meaning and consequence of that p-value number described above is completely independent of when T(y), P(y) were chosen and whether T(y) would be different if y* were different. In only depends on the real concrete facts of the functional form of T(y) and P(y) and the numerical values of y*.
Frequentism leads to a different conclusion. Frequentists believe that the true meaning of that p-value number changes based on when the researcher chose T(y). Presumably if the researcher bangs their head and can’t remember when T(y) was chosen then the data is useless for frequentists!
They also believe the true meaning of the p-value changes if we lived in a different universe with different y*. How they acquired this knowledge of other universes isn’t mentioned, but it’s amazing to me that Frequentists can be so consistently wrong about this universe, yet are experts on alternate universes.
So as I get tired of repeating, if the Garden of Forked path critique makes sense to frequentists, then frequentism is bogus.
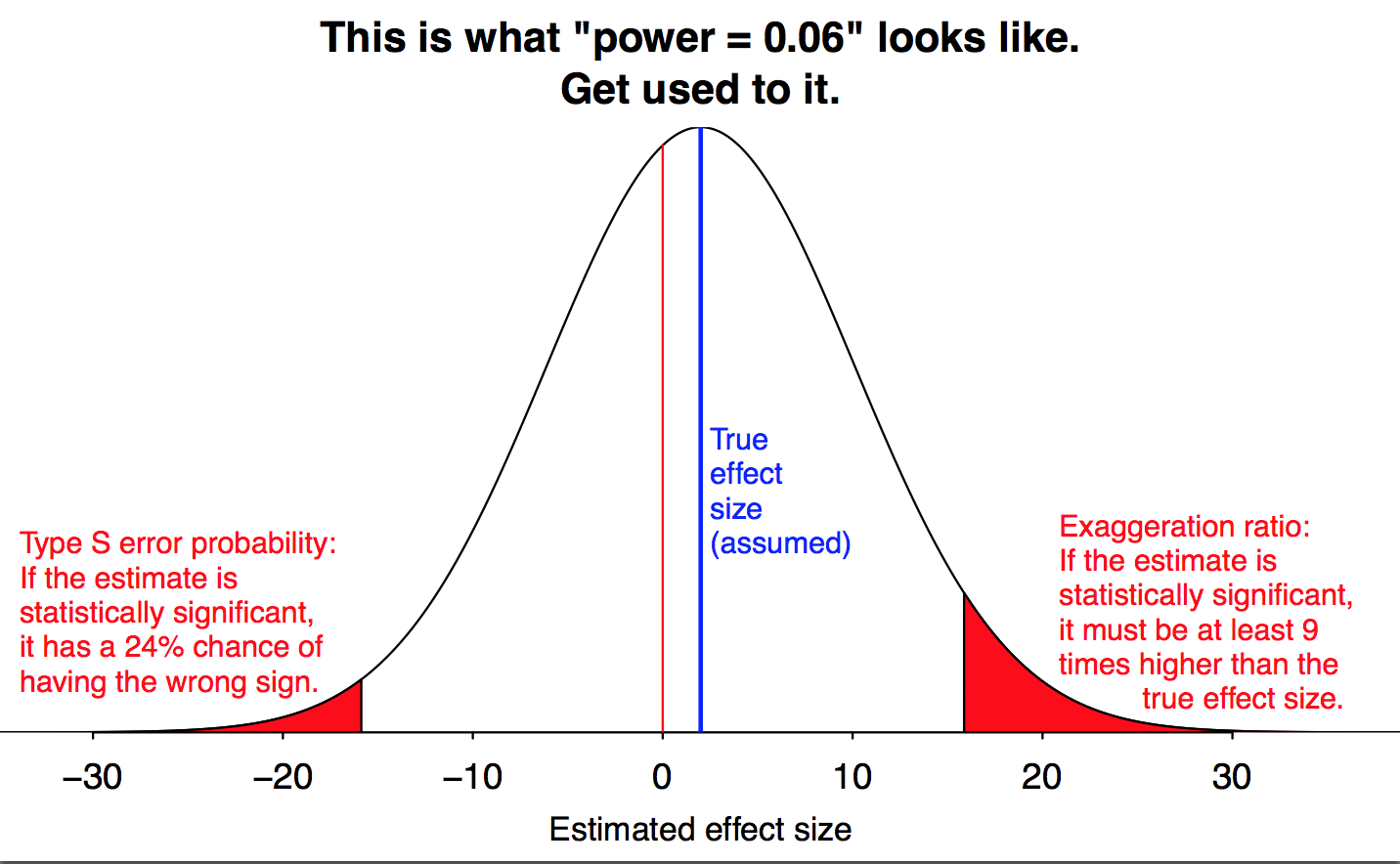
Some comments: I think that the graph says little about the actual properties of the test regarding type II probabilities. The power must be thought of as a function, not a scalar. If the statistical test is consistent and the sequence of power curves is smooth, then if you consider an alternative value in H1 close enough to the null, the power will be close to alpha (the significance level) and moving away you will get power curves near one (for a large samples and consistent tests). So near the null power is typically close to 0.05 (the whole curve of power converges to a step function alpha at the null and one at the alterntive area, but this happens in the limit, with finite samples the change can be smooth). There is nothing anomalous with this. If you want to the power of statistical tests near the null, it has little meaning to compute the power in an standard way. You need to use a more sophisticated device such as limit power based on a sequence of alternatives converging to the null type Pitman. But if you still prefer to use the standard power function, then the graph is a clear indication that one must not consider power at an isolated point, this is why Newman searched for uniformly most powerful test. Uniformity matters for decisions about testing procedures.
Finally, it is true that there are other criteria; power is not the only property one can use to compare tests. But this does not mean that Power is irrelevant. Power is relevant not only in a frequentist context; it is also equally relevant in a Bayesian context. Probability of type I error and type II error matters whenever one takes a binary decision, such as buy H0 versus H1, independently of the type of test.
My feeling is that there is too much noise gossiping about power and p-values, actually much to do about nothing. Mathematical statistics has rigorously built all these concepts. Some practitioners may interpret these concepts wrongly, that is another issue. But the tools work perfectly well, if one knows what is doing.
Jose:
I have no interest in type 1 or type 2 errors, nor do I really have interest in power, except that it is a term that people are familiar with, hence it can be useful for communication. I have no interest in null or alternative hypotheses, and I believe that this framework is distracting and has led to decades of confusion. For further discussion of these issues, see my recent paper with Carlin.
I guess what I’m saying is, it’s fine for you to do what you are doing and work within your framework, but your comment above are irrelevant to my concerns. Your comment lives within a world of null hypothesis significance testing, a world which I think we would be best to leave behind.
Actually, my comment refers to the graph above, and the increasing critiques to the classical statistical theory, a theory that is too well built as to suffer from any these problems, if properly applied. If some practitioners use it wrongly, then statistical teaching is the activity that requires improvement, you can blame the messenger but not the message, for in this case the message is crystal clear.
About the framework issue, no matter which type of hypothesis you test, you need similar tools. Even in the context of nonparametric statistics one finds power functions, local alternatives, etc, not to speak of Bayesian inference. One finds related issues, even in the context of discrimination analysis. The researcher needs to make a decision, either to treat similarly the error probability for all alternative decisions, or protect specially one (the null) fixing alpha, and try to get as good as possible for the others. When choosing a testing methodology, one needs probability skills using these tools appropriately, but they must be studied to asses how good the method is. I think that new tests where these issues are not studied, must not be used yet by applied researchers, at least not until all these features are explored in detail. Naturally, one can use other preference criteria to motivate some testing procedure, not error probabilities, but in the end this is a feature that needs to be checked.
Jose:
Yes, I’m making decisions. No, I’m not testing hypotheses. No, I don’t care about power. No, I have no alpha to fix. No, I’m not choosing a testing methodology. You can look at my books and applied research articles to see what I do do, but it’s not any of the things you’re talking about. The classical statistical theory may be well built, as you claim, but it doesn’t answer the questions I want to answer. It doesn’t let me assess changes in public opinion or predict radon levels or estimate the incumbency advantage or . . .
If the classical theory works for you, fine, go for it. You should just be aware that others such as myself have success working in other frameworks, and I think these other frameworks can give useful insight into problems such as all those crap studies that get published with “p less than 0.05.” Hence my graph.
> … or predict radon levels …
Andrew,
This a bit off-topic but looking at your 2006 paper, Figure 1 shows some counties where data is sparse. Do you perceive any utility to explicitly incorporating spatial distributions of radon and uranium levels rather segmenting data by county? (I haven’t thought this through so bear with me…) For example, one could create thin-plate spline representations (regularized with regularization param chosen by cross-validation) of Rn(lat,lon) and U(lat,lon) from the data to fill in regions where the data is sparse. You might be better off using a basis with local support than using TPS. My point is that there could be a benefit to explicitly incorporating the geographic info in the data.
(That reminds me of the Huai River “discontinuity” problem. I’m thinking that there are better bases than the authors used for their analysis. That they didn’t deal with atmospheric mass transfer seems a far bigger problem to me – as is that they didn’t assess their discontinuity hypothesis anywhere other than at the river – but their choice of model functions doesn’t help. Or even they did a LOESS fit to the data, would they still perceive a discontinuity at the river?)
Chris:
Yes, we looked into spatial correlation between and within counties. I don’t recall if all of this went into our papers on the topic; we tried out a lot of analyses and some ideas were only a little bit helpful so we didn’t follow them up. None of our spatial models were fancy, though, it was just simple spatial autocorrelations.
Garden of forking paths … ? (Partly kidding, partly curious whether this could fall into that category …)
It was only an exploratory study. Again, only partly kidding.
Andrew, please do not get me wrong. Any risk measure to asses the ability of a test to do its job is useful, but I do not think that the procedures in your paper with Carlin are substitutes, but complements to the standard approaches.
Jose: “Mathematical statistics has rigorously built all these concepts.” A quick look at the history of frequentist statistics and the origins of null hypothesis significance testing will show that this is completely wrong.
That is the problem, you can’t take a “quick look”, you need actually to get some background in measure theory and functional analysis in order to grasp the subtle features of the theory. This is not a matter of faith, it is a mathematical axiomatic building. Personal desavenences between initial contributors, e.g. Fisher and Neyman, have nothing to do with the correction of the involved tools.
Jose:
I agree with “you can’t take a “quick look”” but not “you need actually to get some background in measure theory and functional analysis”.
Five or ten years ago I would have agreed with you on both (so I did get some of both), but currently with fast computing most of whats important in applying statistics can be demonstrated computationally. (Or that’s my claim above.)
And most of what I did get out of measure theory and functional analysis was that it really did not apply to the finite universe I find myself in.
Keith. I understand your point, but this is not enough. Universe may be finite or not, but if you are looking for an optimal function-rule you need functional analysis, as you are doing decision theory in Lp spaces, Orlic spaces, or whatever space of functions where your rules belong. As a user you can skip it, but you need it if your goal is to criticize methods with optimality properties working in such spaces. Now, one can run some few simulations and hope for the best, but this is not a sound alternative to a formal building. I do not say simulations are useless on the contrary all theoretical papers should include simulations. But if there is a rigorous building on optimal tests which works well, both from a theoretical perspective and also in simulations, it does not much sense use heuristic approaches as an alternative. After all, the criticism is just because some people uses classical tests wrongly, but this is not a problem of the method, is a teaching issue. I agree that new criteria provide complementary information about testing, but they do not undermine (they can’t) older rigorously and we’ll built tools.
Jose:
I did mean to suggest such math was unhelpful but rather not strictly necessary for most work in applying statistics.
For stuff like Reproducing Kernel Hilbert Spaces and all that http://www.stat.wisc.edu/~wahba/talks1/fisher.14/ such math likely is necessary – but few likely need to get to that level.
This conversation seems to have gone in an odd direction from my comment above. My point was just that the standard frequentist NHST procedure wasn’t ever designed, it just grew out of Fisher’s and Neyman/Pearson’s procedures.