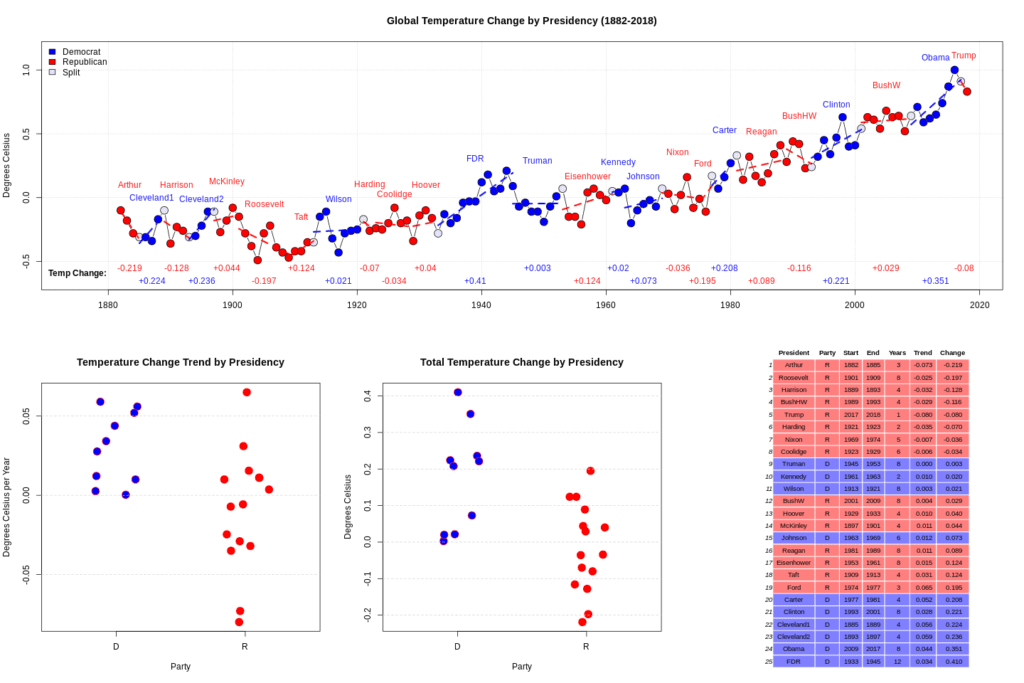
An anonymous blog commenter sends the above graph and writes:
I was looking at the global temperature record and noticed an odd correlation the other day. Basically, I calculated the temperature trend for each presidency and multiplied by the number of years to get a “total temperature change”. If there was more than one president for a given year it was counted for both. I didn’t play around with different statistics to measure the amount of change, including/excluding the “split” years, etc. Maybe other ways of looking at it yield different results, this is just the first thing I did.
It turned out all 8 administrations who oversaw a cooling trend were Republican. There has never been a Democrat president who oversaw a cooling global temperature. Also, the top 6 warming presidencies were all Democrats.
I have no idea what it means but thought it may be of interest.
My first thought, beyond simply random patterns showing up with small N, is that thing that Larry Bartels noticed a few years ago, that in recent decades the economy has grown faster under Democratic presidents than Republican presidents. But the time scale does not work to map this to global warming. CO2 emissions, maybe, but I wouldn’t think it would show up in the global temperature so directly as that.
So I’d just describe this data pattern as “one of those things.” My correspondent writes:
I expect to hear it dismissed as a “spurious correlation”, but usually I hear that argument used for correlations that people “don’t like” (it sounds strange/ridiculous) and it is never really explained further. It seems to me if you want to make a valid argument that a correlation is “spurious” you still need to identify the unknown third factor though.
In this case I don’t know that you need to specify an unknown third factor, as maybe you can see this sort of pattern just from random numbers, if you look at enough things. Forking paths and all that. Also there were a lot of Republican presidents in the early years of this time series, back before global warming started to take off. Also, I haven’t checked the numbers in the graph myself.
There is the issue that political parties have had shifting policies over that time period. Roosevelt or Eisenhower could likely secure Democratic nominations in 2020. Additionally, although the executive has significant influence on economic activity, the legislature has an arguably more meaningful role.
Theodore Roosevelt, I meant to say. FDR would be a shoo-in.
Spurious correlations are particularly likely here because the temperature changes are not iid. The temperature time series has a number of patterns. There is the flat portion in the early part noticed by Andrew. There is also a small decline from 1940 to 1970 (give or take). And there is the flat portion following 1999. The rest of the time series is upward sloping.
Our feelings for statistical significance are heavily shaped by iid reasoning, such as flipping a coin, so we are particularly susceptible to error when looking at correlations between time series with patterns in them.
At what point would you say this is not spurious then? What if not only all democrat administrations had positive trends but also all republican administrations had negative trends?
Being a good Bayesian, I would say that no amount of statistical analysis nor any possible result from this data set would convince me there is something here.
A president is only one part of the US Government. The US Government is only one part of world governance. Climate fluctuations are dominated by very large, long-term, planet-wide factors such volcanic eruptions and ENSO effects (see Harold Brooks’s excellent post), the US Government’s policies regarding climate change vary little administration to administration, US Government policies have very little effect on anything climatic (a fortiori in the early part of the sample), and any effects of US Government policy act with very long lags.
A big part of the recent short-term “trends” is the timing of a major volcanic eruption (Pinatubo) cooling the end of GHW Bush/beginning of Clinton, and the two largest El Ninos, that are warm noise on top of the long-term signal, at the end of Clinton and Obama terms, and La Nina (cold noise) at end of GW Bush/beginning of Obama. If you build a model that incorporates the volcanic aerosol and ENSO effects, all of those things disappear.
Why would you want to “disappear” stuff related to climate when looking at climate data?
Noise with respect to a model of an earth without volcanoes and El Ninos, sure. But that isn’t a model of reality so not sure why we should care about it.
On the one hand, your point is valid, were interested in the actual climate, not some idealized version. On the other hand HB provides an explanation of the observed Dem/Rep partitioning that is independent of US president.
IMO as much as I would love it to be otherwise, I’m 99.732% sure that global temp is 92.09316% independent of brand of presidential boxers @97.5% confidence. But it may depend on daily power posing by presidential canine.
Just the same, it would be fun to take tho data and troll RealClimate just to see Gavin have a conniption.
What model of reality provides a mechanism by which Democratic presidential administrations in the USA make volcanoes erupt?
I suppose one could imagine a way in which El Nino tilts the election toward Democrats? Maybe we should postulate a reverse causal relationship: flat temperatures benefit Democrats in elections, and rising temperatures benefit Republicans!
It would be nice to have the data (so I don’t have to read it off the graph and enter it by hand), but the numbers vs graph seem a bit strange to me. For example, Wilson shows a positive number but the temperature is lower at the end of his administration than at the beginning. I am guessing that the positive number is an average yearly change and most years show an increase. But there was a large decrease that made the overall temperature change negative. So, I think the data bears a closer look.
Looking a little more closely, it appears to have much to do with the split years. I am puzzled why there are such large temperature changes when moving from one administration to the next – this happens a few times. Brings up that topic once again – measurement. Exactly how are these things being measured?
Here is the data: https://pastebin.com/DYGy8tvJ
Here is R code to get the info in the bottom right: https://pastebin.com/8NqJf0Jd
The temperature data was from here: https://data.giss.nasa.gov/gistemp/graphs/graph_data/Global_Mean_Estimates_based_on_Land_and_Ocean_Data/graph.txt
See Global Annual Mean Surface Air Temperature Change at this page: https://data.giss.nasa.gov/gistemp/graphs/
Given the same physical world, Democratic scientists will measure rising temperatures, Republican scientists falling ones.
Interesting hypothesis. I hadn’t thought of this. Perhaps the data is systematically manipulated.
That’s a causal story that is at least not completely ridiculous. You could look at revisions to previous temperature data to look for confirmatory patterns.
THAT’S IT!! because there are no longer any Republican scientists, Global Temp is on the rise!
This is a time series for over 100 years, with lots of noise. Treat it as the right half of an even function, fit a 5th order cosine series using an iid normal noise model and do the analysis on the smoothed function… Anything else is like literal noise mining. (Which this entire exercise is)
For extra credit augment this analysis with results of an 8 and 11 and 14 term series and describe any changes to the results.
Chebyshev polynomials using poly(x,n) in the R lm function also acceptable, and a little less problematic. The whole thing can be done with lm the poly specification and predict function.
It isn’t like I tried out a million analysis to get this result, it popped out at me.
The philosophy of science question I saw with this is: What you do with a surprising pattern in data that really has no reason to exist given what we know?
The outcomes are extreme, either it is coincidence that means literally nothing or it must something that should change our entire worldview since it makes zero sense in the context of the current one. There is like a “thin line between genius and insanity” type of thing going on.
But it isn’t clear to me why exactly it is ok to ignore this correlation, but just because we can think of a plausible explanation for some other correlation it deserves attention.
Taken to the logical conclusion, it seems people here are saying to ignore all correlations in observational data that were not predicted beforehand. But obviously that is not what people do, and they shouldn’t. A key part of science is adducing explanations for patterns what we observe.
“It isn’t like I tried out a million analysis to get this result, it popped out at me.”
You didn’t try a million analyses, but thousands of other people tried millions of other analyses. Given these millions of analyses, what are the odds that one of them would result in something surprising but spurious. Pretty good I think.
Sure, but couldn’t you use that to dismiss any correlation?
Eg, would you respond the same to the “infant mortality” vs “party affiliation” paper brought up below? That relationship is much weaker and the methods look more p-hacked, but some sort of relationship does seem plausible.
On the other hand, if we are always going to dismiss new information that is incompatible with our prior model, isn’t that going to impede progress? At some point I’m sure you agree it would be the model that needs to go, but ignoring all the data that is inconsistent with it prevents us from ever getting to that point.
These are good points, and trouble me as well to some degree.
I think the issue here is simply that any link between these two variables (sitting president, or sitting president’s party, and global temperature change) cannot be clearly established with these data. All datasets of the same sample size and underlying variation are not equal.. at least when it comes to drawing causal inferences. It’s just not clear with these data how these two things could be related, in any structural sense. Whereas a dataset that contains information on incidence of cancer and years spent smoking provides a much more reasonable structural mechanism, even if it contained similar underlying variance and sample size to the one you’ve presented.
I’m not fully satisfied with this answer, would be interested to hear what others have to say. But obviously when you want to make causal claims.. what the variables represent become important; it’s not just about statistical analysis.
In general I have this issue with most empirical economics work, which is my field. Given this pattern you’ve presented, I think the next step would be to get some more data and try to find a better (or just a different) way to measure this relationship. Given that you set out with this specific goal, this should eliminate most concerns a la Garden of Forking Paths. If this was some obscure economic pattern, the next step most economists would take would almost certainly be to write down an economic model that rationalizes this; which is just a waste of time and resources in my opinion. More time should be spent ensuring these findings aren’t spurious, rather than developing some new model of the real world. Once we’ve decided it’s real, then it might be a pattern worth writing a model about.
Anyways… I digress.
“Sure, but couldn’t you use that to dismiss any correlation?”
No.
Magnitudes matter here. Do a back of the envelope calculation of how much effect Teddy Roosevelt’s actions during his first year in office could have affected temperature that year. Lay out each step. Put a number on each step. I can’t believe you could get within orders of magnitudes of the actual change in temperature that year. Therefore, my prior that there is nothing here is incredibly strong and I would need incredibly strong evidence to overcome that prior.
Yes, my concerns are a serious hurdle to any analysis, especially analyses that produce p-values around .05. Therefore, a single run that produces a p-value around .05 proves very little. That is as it should be. The infant mortality study falls in that bucket and I give it little weight. But, a real effect can produce p-values much better than .05 and produce them consistently and robustly, and there will also be evidence supporting other causal links in the theory, and there will be an underlying story that makes sense.
How about this one:
There is some subset of farmers, who usually vote republican, who can swing elections when they tend to vote Democrat. This happens if they expect a dry-hot (drought-ish) period is coming in a few years (the farmers are tuned to nature so have some ability to see the signs of this) so they get more subsidies (or whatever it would be).
It is vague and even if I found out farmers did vote based on that I still wouldn’t be convinced that is *the* explanation since I bet there are other similarly vague ones I can come up with. However, for me it opens the possibility that the correlation is “real” vs being the result of some kind of species-wide multiple comparisons process.
Not sure how this moves the needle. With probability very close to 1, we can make up an ad hoc story to explain any finding. So I don’t see how this helps us distinguish real results from spurious results.
BTW, the tone of my last post was too negative, bordering on obnoxious. Sorry.
But seriously, did you just try filtering the noise out of the dataset by fitting a 5,8,11, and 14 element chebyshev polynomial and then predicting from the polynomial and seeing if the correlation remains? I’ll give you some R hints:
mod5 = lm(temp ~ poly(year-1950,5), data=mydata)
pred5 = predict(mod5,newdata=data.frame(year=mydata$year))
then run your analysis on pred5 and pred8 and pred11 and pred14… each one “retains more noise” in the sense that the smoothed predictions can vary more rapidly.
If your analysis requires detailed “noise” for its results, vs your analysis continues to be valid for less noisy smoothed results… it’s two very different things.
The derivative of a function (year on year difference in this case) is an extremely noisy thing. Think about the property of a Fourier series. Derivative of a fourier term is gotten by taking the fourier term and multiplying its coefficient by the frequency. So it amplifies the effect of high frequency variation. If you have any typical iid normal measurement error at all it is almost the only thing left after you do adjacent differences.
How do you know what you are filtering is noise? Sure it might not be part of the trend, doesn’t mean it’s noise (in the sense that it has no meaning, not in a purely statistical sense.)
The interesting question here is what to make of correlations that seemingly are “real” in a given dataset. Let’s suppose for the sake of discussion that this correlation passes these tests of yours. Then the question is what to do next.
The first thing we probably have to take into account is that the temperature *is not what we normally think of as a measured quantity* it’s the output of some model that aggregates the energy in the atmosphere across the entire globe and at every level of the atmosphere, and is based on tens of thousands of what we’d call “measurements” (ie. readings from thermometers). Second, we should consider the *daily* fluctuations in temperature at any given point, which probably ranges from 2 to 5 degrees F (1-2C) near the tropics to potentially 50-70 degrees F (30C) near the poles.
Knowing that we’re trying to aggregate thousands of global measurements taken multiple times per day that vary somewhere between 2 and 30 degrees C daily into one “effective global” number per year using a complex model already tells us that changes in the range of a couple of tenths of degrees C from year to year are most likely meaningless and amount to largely modeling and measurement error. The entire range from 1880 to 1930 should most likely be considered consistent with zero trend + modeling and measurement error just based on this background knowledge alone (and our knowledge of how sparse the thermometer readers were in 1890 or 1900 or 1910 etc).
So, it’s a good place to start with to say “what does the smoothed trend using only around 5-10 degrees of freedom in a polynomial/fourier series tell us about what happened?
5th degree: https://i.ibb.co/8s7NPwG/temp-By-Pres.png
14th degree: https://i.ibb.co/30T6bkG/temp-By-Pres.png
20th degree: https://i.ibb.co/3Sj8wwh/temp-By-Pres.png
25th degree: https://i.ibb.co/YbyJN3p/temp-By-Pres.png
So if you smooth away any info that is shorter than a presidency all the intra-administration trends disappear. The less smoothing the more of the correlation remains.
There is something circular going on here. You are assuming that 2-12 year long trends in the temperature data are “noise”, that is something this correlation would suggest is not true if real.
Well which of these series is more “correct” in the sense of being an accurate representation of the actual physical state? The smoothed versions use information from the past and the future to estimate the present whereas the non smoothed versions use what exactly? Do you know? I’m interested in what the temperature variable actually means.
Lets put this question another way.
Imagine you are a policeman. Should you incarcerate everyone who look suspicious to you? Or should you only incarcerate people if you have sufficient evidence against them other then their suspicious look?
In this case it is more like we are looking for the hacker running the most sophisticated islamic terrorist organization in the world. However, all the evidence points to the nice old middle-american lady who has gone to protestant church every day, can’t even use an atm, and raised a big family of sons and daughters in the US military.
It is that the “evidence” doesn’t make sense in the context of our prior model, so it gets rejected.
This is a perfectly reasonable Bayesian thing to do though in some circumstances. Jaynes gives some example I can’t remember the details, but similar to imagine there’s a card-shark who can give you a deck of cards, and you shuffle them thoroughly, and then from across the room without touching the deck in any way, can predict each card that you’ll draw off the top.
This seems to be evidence of ESP, but in reality we will simply start a thorough search of the room for hidden cameras or some such trick mechanism. No amount of this person running this trick will convince us that the person has perfect ESP. In some sense there’s evidence around us that they dont: why run a cheap parlor trick when you could run a Hedge Fund and spend your life sailing around on your Super Yacht? So the evidence isn’t all that interesting *in and of itself* it’s the *mechanism* that’s interesting.
I too have had a problem with the idea of a global temperature for awhile. I looked into it a bit the other day wondering how exactly these numbers from 1880, etc were arrived at.
Take this as a case study for one site (just a random page from the first one I clicked):
https://mrcc.illinois.edu/FORTS/histories/AL_Mobile_Doty.pdf
See section 5 here for an overview of the quality control procedures done on the above type of data (many magic numbers, etc):
https://journals.ametsoc.org/doi/10.1175/1520-0477%281997%29078%3C2837%3AAOOTGH%3E2.0.CO%3B2
So does adding another arbitrary layer of smoothing onto this already heavily processed data represent reality any better? I don’t see how it could except on accident.
I don’t know if adding smoothing represents reality better or not. But I imagine it should under certain circumstances. Specifically suppose that there exists a meaningful “true” global mean temperature. Suppose that we have an estimating algorithm for this quantity and it uses only measurements of various types from the year in question to get the value for the year in question. Now suppose that there is algorithmic error involved in the estimate that we can model as IID normal(0,s) for some scale s and that the underlying true temperature changes no faster than some rate R from year to year. Then the calculated rate of change:
t(n)-t(n-1) = a*R + normal(0,sqrt(2)*s)
for a in [-1,1]
whereas the smoothed version will be much closer to a*R
Try it out. Take the smoothed version you calculated with say 25 terms…. add normal noise to it of scale say 0.1 degrees C. Fit a *new* smoothing function to the noisy smoothed version. Compare the adjacent differences with noise and the adjacent differences in the re-smoothed data, to the actual underlying thing (the smoothed with 25 terms data).
IID normal noise has Fourier spectrum that’s flat out to the full Nyquist bandwidth. The smoothed data has Fourier spectrum that rolls off at some intermediate frequency. If the underlying data doesn’t have “real” variation above some frequency, then the smoothed version will be eliminating mostly the IID noise.
So, there are situations where smoothed data should be expected to better represent reality, when your measurements literally have algorithmic and measurement error that dominates the high frequency components.
Interesting, thanks. Thinking of how to tell if this applies to the current problem I realized that other people in the thread can apparently see the effects of short term volcanic eruptions and El Nino events (e.g, https://en.wikipedia.org/wiki/1997%E2%80%9398_El_Ni%C3%B1o_event) in this data.
So if the smoothing process removes/alters the signal from these “known” influences then it would be a step backwards right? I mean it may also remove “real” noise but if it is also removing signal that is bad.
Sure, maybe. If someone can tell me what the actual physical quantity that “Global Temperature” is supposed to approximate, then I’d have an idea of whether El Nino is a “real” signal *in the Global Temperature* data or is in fact noise.
Like for example, suppose “Global Temperature” is C/N * sum(K[i],i,1,N) where K is the kinetic energy of all molecules not currently residing in a solid substance at altitudes greater than 10 meters above mean sea level
Then is ElNino signal or noise? Reading the wikipedia article it looks like ElNino would be signal caused by energy transfer out of the deep ocean into the surface layer of ocean and then the atmosphere.
But if you defined Global Temperature in terms of the sum of kinetic energies of all molecules in the ocean + atmosphere, you’d have to call it measurement noise because heat coming into the atmosphere is coming out of the ocean.
So, at its heart, we have a measurement issue first. Tell me what “global temperature” means.
I think what they want measure is defined here:
Climate Impact of Increasing Atmospheric Carbon Dioxide. J. Hansen1, D. Johnson1, A. Lacis1, S. Lebedeff1, P. Lee1, D. Rind1, G. Russell. Science 28 Aug 1981: Vol. 213, Issue 4511, pp. 957-966 DOI: 10.1126/science.213.4511.957
https://climate-dynamics.org/wp-content/uploads/2016/06/hansen81a.pdf
T_e = [S_0(1 – A)/4*sigma]^0.25 + gamma*H
S_0 = Mean solar insolation = 1367 W/m^2
A = Mean proportion of solar radiation reflected back to space = 0.3
sigma = The Stefan-Boltzmann constant = 5.670367(13)e-8 W/(m^2⋅K^4)
gamma = Mean lapse rate of the atmosphere = 5.5 C/km
H = Mean distance from sea level to the tropopause = 6 km
All averages are over the course of a year and the entire surface.
So it’s “effective radiating temperature” in other words (I think) the temperature of a black body the size of the earth (say sea level radius) that radiates the same total energy to space as the earth does.
I have one problem with their assumption there which is that “determined by the need for infrared emission from the planet to balance absorbed solar radiation”
In the bulk it must, or we’d have RAPID rise in temperature. But to second order we’re talking about trapping energy from the sun and warming the planet, so it should be modified so that the solar influx balances the radiation + absorption.
Influx = Radiation(T_e) + Absorption
Unfortunately, the Absorption is itself the thing we’re most interested in, and it’s not directly measurable, and neither is the effective radiating temperature, so the problem is inherently unidentified as the right hand side of the equation is the sum of two Bayesian parameters.
We can partially solve this by finding ways to estimate absorption and estimate radiation, and thereby come up with tighter posterior intervals, but we’re not going to eliminate this entirely.
Basically in an asymptotic analysis we can drop the Absorption because we can make the whole thing dimensionless by dividing by Influx, and then Absorption/Influx is small, this gives a good way to estimate the approximate size of Radiation(T_e) and therefore T_e but it is very slightly off. However you can perhaps put some kind of bounds on the rate of absorption, so that Absorption/Influx is known to be less than some number, just throwing a random number out there let’s say it’s 0.002 then you’re going to find that the bias caused by ignoring absorption is quite small. so for the moment we’ll leave it at that.
Additionally there’s an error in the typesetting of the equation, equation (1) should have T^4 which is where the T = (…)^(1/4) comes from.
unfortunately, it being a nonlinear equation, you can’t get the effective temperature by averaging the effective temperature of each piece of the earth… You need to integrate the total radiation over the earth, and then take the fourth root of that…
The physicists working on these issues know this stuff, but it’s not always obvious what’s going on “under the blankets” when you get some time-series from a website.
I think ideally they would have stations uniformly sampled over the surface, using the R geosphere and rworldmap packages I checked what 100 stations would look like: https://i.ibb.co/cCvtZJ0/Station-Map.png
Each station never moves over the course of the observations and the instruments are always perfectly calibrated. All the “adjustments” to the data are attempting to make it more like that.
Then the mean and equilibrium/effective temperatures would be calculated like this: https://pastebin.com/b1YJFxJ6
> # Mean Temperature (K)
> mean(SBlaw(Irrad))
[1] 143.9252
>
> # Equilibrium Temperature (K)
> SBlaw(mean(Irrad))
[1] 260.0704
The “mean” temperature is what we would expect to measure “without an atmosphere”, and of course at any one time the blackbody temperature will be zero over half the globe unless we give the surface a heat capacity.
I don’t see an overall mean temperature measured for the moon but this paper reports averages 215.5 K at the equator and 104 K at the poles, so it must be between those values. So I think this value is ok:
https://www.sciencedirect.com/science/article/pii/S0019103516304869
The temperature of the earth based on the measurements is obviously more like 288 K, meaning surface and atmosphere effects account for ~150 K worth of “greenhouse effect” and need to be added to the model. Obviously the night side doesn’t cool to zero as soon as it is out of the sun, etc. Once we have defined that model then we know exactly what the “global temperature” actually refers to.
Yes, the main physically meaningful number here is the SBlaw(mean(Irrad)), That’s the one that tells you what temperature the uniform black-body radiator the size of the earth needs to be at in order to radiate the same amount as the actual radiation.
The other mean(SBlaw(Irrad)) tells you what numbers the individual local thermometers average around, but the hotter ones obviously radiate a lot more and the cooler ones radiate a lot less due to the T^4 law which is why these numbers are so different (144 vs 260 K)
The other bit is that we really want not what is the surface radiation, but rather what is the radiation to space, so for example you could look at the earth from the moon, and measure its radiative brightness like by taking an IR photograph of it… and do this from many angles, and at each point above the surface of the earth, discover what the radiative quantity is there…
the difference in the radiation as seen from the moon and the radiation as measured at the surface is in essence the “greenhouse effect” as some surface radiation is absorbed and converted to kinetic energy in the gas, and some re-reflected back to the earth, etc.
So with all that said, ElNino probably does change the temperature of the gas, and surface, and hence is somewhat of a signal, but *it also violates the equilibrium assumption* as now you could be radiating *more* heat than the solar influx (since you’re basically bringing heat out of the deep ocean) and during LaNina you violate the equilibrium assumption as well because you’re storing heat in the ocean.
So one way to think about this is as modeling error: your assumption is on a relatively short timescale, like a month or so, there is zero net energy put into or taken out of the earth. That’s *how you define your effective temperature* and then, you try to use this equilibrium model to discuss a situation in which you’re explicitly violating that assumption by having heat storage over time scales from decades to millenia (in the ocean, ice pack, etc).
In the past I’ve said that I’m not in favor of the current fad for Global Circulation Models, and would prefer people spend more time on this kind of model, adding 5 or 10 known important effects and estimating coefficients for those, and try to describe the climate with just these 5 or 10 unknowns instead of a GCM which might literally have a million.
One of the real advantages of doing this more explicit smaller scale model is that you can actually run Bayesian posterior distributions over the 5 or 10 parameters, and see how the various effects work relative to each other in terms of contributing to the uncertainty in climate response.
The downside of smoothing is you are screwing up the timing of the data and timing is critical here.
If you impose a 10-year moving average, what year do you assign that average to? Your choice could easily reverse the results. Your choice could shift some of the temperature data up to 10 years. You could easily introduce spurious ESP into the sample where you include temperatures from year t+9 in your calculated temperature at time t.
No, this isn’t a moving average, this is a basis function expansion of the time series. In the fourier case, the high frequency terms are truncated to zero, but there is no phase shift. In the Chebyshev example it’s slightly different, a Chebyshev polynomial *is* a Fourier expansion of a transformed version of the problem. But it still is an orthogonal basis, so truncating the higher order terms doesn’t really affect the values of the coefficients of the lower terms.
Thanks for the correction.
On a more general level, though, does this transform mean that an observation at time t is affected or transformed or altered in some way by nearby observations? Do we know that such a transformation doesn’t subtly affect a time series analysis?
Well, the *observations* aren’t affected by nearby observations, but the *estimates* / (or output of the “predict” function) are. However in the basis expansion method we’re choosing the function that *globally* minimizes squared error (at least when we do least squares, in a Bayesian analysis you get a distribution over possible functions). What happens is by limiting the number of coefficients we limit the degree of “detail” that can be in the function’s we’re considering. In a Bayesian analysis we can put strong priors on the magnitude of the higher order terms thereby getting a more continuous version.
So yes, it uses global information to estimate each value, that’s why it’s so powerful, but no, it doesn’t shift the information forward or backward in time, like you would with say an exponential weighted moving average of the past (which shifts your estimates backwards in time)
I don’t think the size of the object matters.
It seems to me this is what is actually being measured by the various weather stations, so therefore that is the “physically meaningful number”. If we want our theoretical “global average temperature” to match with what we are measuring, we need to calculate the same thing.
RE size if object, in this model it cancels. The size of the object could matter in other models.
Re what’s meaningful. The radiative equivalent temperature tells us about the process of interest, the thermometer readings are indirect measurements that can inform estimates of the quantity of interest, but people often make the mistake of focusing on the measurements as if they were the actual thing of interest. This is in no little part due to Frequentist concepts of measurement as RNG output. What matters here is radiation and energy balance. If you can compute it with a huge array of thermal cameras in space without ever taking a ground level thermometer reading then that’s a good thing.
I agree, but that isn’t where this data comes from. They actually want to be measuring total energy content.
Anyway “global temperature” seems to have (at least) two different meanings then, or the current instrumental record measures something different with the same units. Was this your original point in asking what it means?
Yes, global effective radiative temperature means something totally different than global time averaged mean thermometer reading. I believe most climate data is thermometer readings but that the published global temperatures are estimates of the effective radiative temps calculated from a model incorporating a wide variety of data including thermometer readings, but this means the timeseries you are using is *nothing like* a direct measurement it’s the output of a model with tons of assumptions built in.
The biggest thing that sticks out to me is that global warming trends have a huge time lag between the anthropogenic factors (e.g. CO2 concentration) and observed warming. That’s why reports say that even if we were to stop all CO2 emissions tomorrow, we’d still observe warming over the next 50 to 100 years. So breaking down the global temperature trends by who was the president *at the time of observation* seems to be a completely futile exercise—the warming we observe now, after removing non-human caused trends, is due largely to what happened years or decades ago.
This is a good example of the kind of thing that gets passed around political circles as “proof” that the other side is actually more guilty of the thing the other side campaigns on (e.g. addressing global warming for Democrats).
Naked correlations like these are usually presented (coyly and dishonestly IMO) as merely “interesting” rather than causal, but whoever prepared this knows exactly how the vast majority of non statistically literate people will interpret the information. If you have the ability to do this level of analysis, you bear the responsibility to at least attempt to interpret the results using sound methodology.
https://statmodeling.stat.columbia.edu/2015/04/21/feather-bathroom-scale-kangaroo/
The burden of evidence seems misplaced. If you want people to take seriously the suggestion that the color of the feather should affect the reading on the scale, there needs to be some kind of plausible mechanism for that.
yup. obligatory reference:
http://www.tylervigen.com/spurious-correlations
Several years ago, a similarly-designed study reported that Republican presidencies were associated with elevated infant mortality rates. You might want to consult it for context.
The study is available on pubmed: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4052132/
It was widely covered in the news (Washington Post, Atlantic, and others) but has received relatively few citations since.
The most obvious problem I can see with this is that the very idea of mapping global climate change to American presidencies implies an assumption that United States presidencies can have that level of influence on climate change. Basically, it ignores that the entire rest of the world exists, despite there being many other nations- most notably China- that have large emissions that might influence climate change. As such, I’d say the “unknown third factor” suggested to be mentioned before dismissal of a correlation as spurious would be the existence of the entire rest of the world.
The US does have an outsized contribution to the temperature data, so it is possible that the president could have an exceptionally large effect: https://en.wikipedia.org/wiki/Global_Historical_Climatology_Network
But I really don’t see any reason there should be an effect. AFAIK, temperature records were not political until very recently and as others have mentioned the policies of the two parties are not constant anyway.
By “unknown third factor” I meant something that affects both temperature and party affiliation of the US president.
Anoneuoid
You raise some interesting points. I’ve explored the data a bit. The strength of your “findings” does depend on how you treat the data when presidencies change – but for the most part, the pattern you are citing is true. As a number of people point out, the story is somewhat implausible. I think we could state that even more strongly – I don’t believe the US President can have this large of an impact and certainly not within this time frame. Still the empirical picture is a strong one – too strong to just dismiss as noise and move on. Well, that is debatable – Andrew dismissed it as noise. And, I don’t intend to spend any time trying to invent stories that might explain this pattern, so I guess I think it is noise as well.
But I think your point is that just dismissing surprising/implausible findings like this might rule out new discovery. I think you are right to point out that danger. I think the best course of action is that there is a place for discoveries such as this – rather than overstating that a “significant” finding has been found, it is simply an odd empirical observation. If people find it worthy enough, then it would warrant follow-up research to see if it can be tied to a plausible theory or if it can be replicated in some fashion. But somebody needs to find it worthy enough to do that.
I think I would put this in the same class as ESP, power poses, facial expression, shark attacks, etc. All involve an empirical observation, all have suspect theoretical foundations. If your point is that we shouldn’t dismiss them just because they seem implausible, then I think I agree. However, I wouldn’t treat them as a finding of anything real either. That would just be “fooled by randomness.” There must be enough possibility that the finding is real to warrant further investigation. And that depends on how other researchers (let’s leave the media out of it) view it. As a sociologist (I’m not one) might say, all knowledge is socially constructed. So, whether the impact of Presidential party on global warming is real will depend on how the scientific community reacts to it.
The sad part is that we have seen too many research areas where the community has found it worthy to pursue lines of inquiry because they garner headlines, grants, publications, etc., regardless of whether they really believe there is underlying merit. In other words, we seem to have very poor filters for determining what “surprising” findings receive further research.
Despite what is said in the media, the Democrats have consistently backed policies that shut down green energy sources, particularly nuclear power.
NYS Democrat Gov Cuomo plans on shutting down Indian Point nuclear power plant (NPP) which generates 1/4 the electricity of NYC and Westchester County (total pop 10 million).
The Democratic government in California shut down one NPP a couple of years ago and plans on shutting down their last NPP in a few years.
It would be best to shut down all coal powered electric power plants before shutting down NPPs. *That would be the green policy*.
Also, it was a strictly political move by the Obama administration in 2011 that closed down the construction of the Yucca Mountain (Nevada) nuclear storage facility. Thanks to this stupid move, NPPs have to store everything locally on-site as opposed to deep in a mountain in Nevada.
The Trump administration has thankfully resumed construction of the Yucca Mountain facility but the move to store nuclear waste off-site has been delayed for a number of years.
The Trump administration policy is to keep all NPPs on-line.
Not that surprising. Democrats are elected when the economy is bad to bring it back. Republicans are elected when times are good to preside over recessions. Next recession, just about now?
It turns out that El Nino and La Nina cycles have a major influence on world temperatures. The Southern Oscillation Index (SOI)is one measure I found which is apparently related to these phenomena. Sure enough it is a strong influence on the global temperature change (in the data provided by Anoneuoid above). When that is put into a model, it dominates the other effects. Republican presidencies still have a statistically significant negative relationship with global temperature change (p=.045, but that seems like noise to me) and democratic presidencies are very far from significance.
See my idea here.
Assume farmers are able to somewhat predict El Ninos and for some reason prefer a certain party to be in control during those years. So then the political effect is caused by the El Nino effect. I am in no way saying something along those lines is actually the case but isn’t this analysis going to hide something like that?
It’s a plausible explanatory mechanism, so you can investigate that mechanism using vote estimates for farmers in each election, or other similar groups. warning though, in 1900 almost everyone in the US was a farmer by 1960 almost no one in the US was a farmer.
Now you are starting to sound like Cuddy, Wasnink, et al. These are far fetched scenarios in the face of evidence that you are looking at noise. It’s one thing to say that we should not dismiss strange and striking results just because they don’t match our priors. It is quite another thing to dig in and insist that the “finding” is real, even when it starts falling apart as soon as additional data and/or modeling approaches are used. Yes, science needs surprises to move forward at times – but it also needs ideas to be dropped when they are looking spurious. I think you’ve become attached to the idea you initially put out as a provocative question.
It really isn’t that I am attached to it. Before that idea I really had no possible way of fitting a this correlation into my understanding though. The correlation just needed to be rejected because it “made no sense”.
I don’t understand how this process can tell us there is no relationship between party and upcoming temperature trend. Someone also suggested adjusting the data to remove volcanic activity, why? These are possibly parts of the climate/weather that could link the party and temperature trend.
So maybe I misunderstand, but if the scenario I devised is correct would your method be able to reveal the true reason for this correlation or would it hide it? I think it would obscure the truth (in the universe were farmers are predicting El Nino’s and voting based on it), so there is something faulty about the approach.
I think almost everyone here assumes you are looking at causality like : President Is Elected —-> Temperature Changes and they think basically “there is no plausible mechanism for this, the magnitudes are all wrong… it’s gotta be spurious”
but that isn’t your personal mechanistic idea, so … keep going with your mechanism. Chase it down in some more detail.
I don’t think that’s an accurate description of what’s going on. This isn’t “defend my sexy theory that’s in all the textbooks” this is straightforward exploratory data analysis, so now the analysis has generated a plausible mechanism hypothesis that can be investigated by pulling in more data… It’s how science should work. Anoneuoid isn’t defending this possibly spurious result well past the point where it’s shown to be spurious, just investigating whether it is or isn’t spurious.
OK. So, we have to see if farmers are able to predict El Nino. Then, see if farmers prefer one party over another. If both can be supported, then we have a mechanism by which the apparent “spurious” result is not spurious. Don’t you think that we can always find another chain of logical links that could “explain” what seems anomalous? Certainly that is what has been done with power pose – every time the effect is not replicated, another potential intervening factor can be found that might explain the results.
I guess you’re saying this is how science progresses. And it is. Sometimes. But when do we reach a point where it is no longer productive to keep inventing possible reasons for the exploratory results and spend our energy on something else? My point is that this involves the sociology of science – it is not a matter than can be decided by statistical results alone. And, our institutions within which science is practiced are highly imperfect. Bad ideas (perhaps you can find a better word than “bad”) don’t necessarily get weeded out.
Yes, of course you cannot support a theory using the same data used to develop it. The scientific method:
1) Abduce (Guess) an explanation for the observations.
2) Deduce different/new predictions about future/other data from this explanation.
– Bayes’rule tells us the more surprising (which usually requires precision) the predictions are the better.
3) Collect the other observations to check these predictions.
I will never make mistakes like Wansink, et al because I have a philosophy of science that is extremely robust to this source of error. In fact it leads me to reject far more of modern research as invalid than most people can handle.
It is very rare to see models tested via bona fide predictions these days. Researchers get stuck in step 1 and circularly verify their models with the same data, or only come up with vague/unsurprising predictions (that are consistent with many other explanations) in step 2 so the “tests” are very weak.
Yes, there is definitely another dimension here I am trying to get at. How can this be done in a principled fashion? It is like there is a step 0 missing from above. The real first step is choosing which observations to spend time on.
Well, whether it’s “worth it” to spend time on trying to explain a particular phenomenon is definitely a personal value judgement. So if Anoneuoid wants to chase this down to his (her?) satisfaction, I think that’s a reasonable thing to do.
I think we need to make the distinction between “This is how things are and I’m going to tweak my hypothesis in the face of any evidence so it can’t be killed” vs “I wonder how things are, could it be X, and if not could it be Y, or could it be Z or something else???”
“So if Anoneuoid wants to chase this down to his (her?) satisfaction”
Did you just assume Anoneuoid is binary? I can’t believe people are still doing this in 2019. That is so 2016.
It is one of those things. Look at the period of Reagan and Bush the elder. The way the blogger counts it, it is up for Reagan and down for Bush. If you combine the two, it is up for whole period. The year to year variation in warming has to do with things like El Nino. Should we believe that Republican blowhard affect El Nino?
Apart from the obvious problems with small N for each presidential period, global warming numbers are GLOBAL, and while US contribution is high it is not the only influence. Attributing to a president of a particular colour in the US is very myopic. What nonsense! Take the bump in the 40s – the massive rise in industrial activity in WW2 both Europe, Japan and US like to have given it a push. And is the rise in industrialization in both China and India not a real consideration? As other have pointed out there are other meteorological and geological events that move the dial only for a period. It would be more useful if this current US administration would at least acknowledge global warming.
Everyone assumes causality one way… Anoneuoid hypothesis is that temperature causes vote swings not that presidents cause climate…
Is this getting dangerously close to admitting the correlation is probably spurious?
If you need a hypothesis as convoluted and tenuous as this, doesn’t that suggest there isn’t really something there and we are just making things up? The most direct causation model is the one everyone assumed (that’s why they assumed it). There are a thousand other ad hoc hypotheses we could have created, and this farmer hypothesis doesn’t strike me as being even in the top 20.
So what does making up goofy ad hoc hypotheses accomplish?
BTW, it hasn’t even been shown that there is anything statistically significant here. The temperature data is a complicated time-series with time-varying properties. The presidential data also has patterns. This seems like fertile breeding grounds for a spurious correlation. All you need is for one of the patterns in the temperature data to line up with one of the patterns in the presidential data. To take an extreme example, imagine that all the presidents in the first half were Republicans while all of them were Democrats in the second half. Since the temperature data is flat in the first half, it would generate a spurious correlation. All this needs to be statistically modeled … a very tall task.
I’m beginning to think we are being trolled. A very subtle and imaginative trolling of the highest order, I’ll grant you.
As mentioned in the OP, a “spurious” correlation can still be “real”, it is just that a third factor C explains the relationship and there is no causal connection between A and B. That is different from: “if you look at enough data you will eventually find a correlation and even if you personally didn’t look someone else looked so we need to adjust our p-value for that”. Multiple comparisons adjustments never made sense to me for exactly this reason.
Please see my comment here for the role I give this type of activity in the scientific method.
The only way I could be trolling is if I actually did data mine this correlation, which I didn’t (if I had it would have held zero interest to me). I can’t prove I didn’t, so there’s that. I could have (but declined to) easily had a career producing medical “discoveries” like that though if I wanted.
It took me awhile to come up with that one. What is number 1?
“What is number 1?”
Good challenge.
How about the data is manipulated where a Democratic administration, at least implicity, pressured record-keepers to report higher temperatures. Someone else proposed this, or something very like it elsewhere. Or the inverse that a Republican administration pressures record-keepers to depress temperature readings and temperatures rebound after a change in administration.
Hypothesis number 2:
Changes in budgetary priorities means less money is spent on maintaining weather instruments in Democrat administrations and so the instruments read higher than they should (dirty housings are darker and so increase internal temperatures). During Republican administrations, the instruments are cleaned better and so temperature readings drop. Need to make up a reason why Democrats want to spend less on instrument maintenance than Republicans do … shouldn’t be hard.
Hypothesis number 3:
When temperatures drop, crop yields and farm profits fall and the economy slows down. Voters tend to hold Republicans responsible for the economy but not Democrats. Temperatures are mean reverting to the trend. So when temperatures temporarily drop below trend, Republicans are replaced by Democrats and the rebound occurs during a Democratic administration. The same does not happen to Democrats because … reasons.
Hypothesis number 4:
Republicans are good for the economy and Democrats are bad for the economy. (Not empirically true, but that hasn’t stopped us so far.) The economy revs up under Republicans and energy usage increase causing a increase in greenhouse gasses and an increase in temperature. But the increase is lagged so the increase in temperature occurs during the next administration and voters get tired of having one party in power so they like to switch parties from election to election.
Hypothesis number 5:
Volcanos! (Volcanoes?)
Volcanic eruptions increase global temperatures (this has the advantage of actually being true).
Voters vote for Democratic presidents following volcanic eruptions because … reasons!
The hardest part for me is believing that the stance of the two parties has been consistent enough on the relevant position since 1880 for any of these explanations to really work (including my “farmers voting for subsidies” one). Maybe I underestimate how consistent the positions have been on certain tariffs/subsidies/whatever though.
But anyway, I definitely do not feel inspired to go dig up info on all these putative intermediate mechanisms to see which would survive. However, I still don’t get exactly what rule I am using that makes me act/think/feel that way about this correlation.
I agree. It is easy to make up silly hypotheses, and I don’t think any of these rise above the silly level. That is my point. Making up silly hypotheses doesn’t move us forward. Indeed, the more you think about them the sillier they sound.
Terry:
Silly they may sound, but link them up with Gladwell, NPR, Ted, PNAS, etc., and they can get lots of publicity and influence.
Terry wrote, “Volcanic eruptions increase global temperatures (this has the advantage of actually being true).”
No, it is actually false. The big volcanic eruptions (Pinatubo 1991, cooling trend 1992) produce a short-term global cooling trend due to injection of sulfate aerosols into the stratosphere. These aersols reflect more sunlight back to space rather than being absorbed at the surface for warming. Fact: The climate computers modellers have to tweak-in higher than observed sulfate aerosols to cool their model runs when studying the past.
Thanks for the correction. I was going from memory.
But the hypothesis is so great that being 180 degrees wrong is no problem. Just reverse that sign and another sign somewhere else and we are good to go!
The hypothesis is so great that it produces truth no matter what the facts are. Garbage In, Truth Out! GITO!
No, I think this was just a politically charged topic. Suppose instead of global temperature it had been global Coffee Bean yield? No one would be getting their undies in a twist and would instead be discussing the question of how you can determine if something is “real” vs a spurious correlation.
I think it is pretty obvious what is going on here. When temperature goes up, it increases the number of shark attacks. That causes people to vote republican, so at the end of a rapid temperature growth period, a republican president gets elected. Then temperature growth slows down again, shark attacks decrease, …
Wins thread.
+1
I can’t resist telling the joke my lawyer cousin once told:
Question: Why didn’t the shark eat the lawyer?
Answer: Professional courtesy.
I agree about forking paths. The intercept of almost every administration is higher than the intercept of the previous, so the trends surely wouldn’t be nearly so dramatic accounting for time. There are many other predictors that also might make the trend disappear in an actual regression analysis, like accounting for who controlled congress or the average price of fossil fuels. In fact, the data as presented are entirely consistent with the hypothesis that Republican presidents are worse for the environment: there has to be some time lag between the implementation of a set of policies and their environmental effects, as mediated by changes in industry and consumer practices. Maybe W’s policies resulted in higher Obama emissions, while Obama’s policies resulted in falling Trump emissions.
Buja, Cook, Hofmann, Lawrence, Lee, Swayne, Wickham have a nice 2009 paper in Philosophical Transactions of The Royal Society, A on “Statistical inference for exploratory data analysis and model diagnostics” that could be applied here nicely. Here’s one thing how this could be done. Keep the time series constant but write down a simple random model for republican and democratic presidential periods. Construct a number (49 or 99, say) of artificial datasets using the same time series but with different red and blue periods according to the random model. Then show all 50 or 100 datasets including the real one to one or more statisticians who haven’t seen the real dataset before and ask them to nominate a certain number (5%, say) of datasets that look special in terms of the red/blue pattern. If the real dataset is among them, one could declare the real pattern “significant”. Still then of course this is not strong evidence that something is going on there, because there’s still a forking paths issue with having picked a dataset in the first place that looks somewhat “special”. However, I can well imagine in this case that the result of such a procedure may turn out insignificant, in which case it is pretty clear that the pattern cannot be distinguished from randomness. (A more sophisticated version would also use a model for generating the time series – maybe using parametric bootstrap -, but then the real dataset may be picked for reasons other than the red/blue pattern only.)
This seems like it side-steps the issue. I would want to know why the “experts” are ranking/voting the way they did. What principles are being used to determine what looks interesting?
This has a very simple explanation, we just need to think in terms of embodied cognition.
Democrats are perceived as warm and tend to favor change. Republicans are perceived as cold and tend to favor stability. Thus, after a period of cooling or stable temperatures, the voters are eager for warmth and choose Democrats. After a period of noticeable increases in temperature, the voters are eager for a return to stability and a cooling down, and vote Republican.
Who wants to be my co-author?
Ben:
Do an experiment on some undergraduates and Mechanical Turk participants, and you got yourself a Psychological Science paper. Put in some differential equations and a power law, and you’re ready for Phys Rev E, or Science/Nature/PNAS, or, failing that, Arxiv and publicity in Technology Review.
“A possible theoretical explanation for political instability”! Damn, that title’s already taken.
Fantastic! We can do a between subjects design where the undergrads are placed into different temperature rooms, then they watch a mock political debate between a Democrat and a Republican and identify which they like better. Theory predicts more support for Democrats when the rooms are lower in temperature. We can double our sample size by combining students from both psychology and political science courses.
But, we should also test to see if the perceived warmth or coolness of the debate host has an affect on the significance of the temperature effect. Implicit social cognition theory predicts that we might have a moderator named “moderator”.
Measure perceived warmth on a scale of 1 to 10 and divide the sample into bins based on various cutoffs.
See which cutoffs best fit the data. Test 1 to five different cutoffs.
Ask about political alignment using a lef/right scale from 1 to 100. Bin the sample by cutoffs using a similar technique to determine the best cutoffs.
You increase power when you try more cutoffs because you will identify the most powerful cutoffs.
Ben:
“Theory predicts more support for Democrats when the rooms are lower in temperature,” but if we saw the opposite pattern, or any interaction whatsoever, that would be consistent with the theory too!
This is too perfect.
Thanks. I’m tempted to write this up and shop it around :)
I just realized that 3/4 Democrat outliers can be “explained” due to serving a partial term. These are also the only presidents running as Democrat to serve a partial term during the period we have temperature data for:
Truman: Succeeded when FDR died
Kennedy: Died in office
Johnson: Succeeded over when Kennedy died
That leaves only one exception:
Wilson: Two full terms
Another weak attempt to shift blame. the GOP and GOP voters are to to blame for inaction on climate change. but why wouldn’t the even r on the side of caution on this matter.? Misinformation decide there was another deeper reason. You can’t blame a wolf for behaving like a wolf. Fox news the oil industry, despite their nasty insidious rolls, arejust doing what they do. The real question is why was the filthy Republican unwilling to even consider the possibility that this might be happening. Answer that and you getting to the heart of the matter.
Update with 2019:
https://i.ibb.co/gD01GqN/temp-By-Pres2019.png
Two unrelated cycles are accidentally somewhat in synchrony: (a) the periodicity of solar maxima, which affect earth’s atmospheric; and (b) the periodicity of natural economic contraction points, which occur every 42 quarters and have a strong impact on the presidential election. Solar maxima naturally occur in spans of about 11 years (averaging 10.9 years between 1880 and 2018), each time causing the atmospheric temperature to rise 1–2 years later before renewed cooling occurs. This is very close to the 10.5-year cycle for natural economic contractions. In the 20th century, both patterns happened to be in pretty good alignment. Whichever party is in office in the wake of a contraction usually loses. Whichever party is in office in the wake of a solar maximum sees the atmospheric temperature rise. In these data, 53.5% of years are Republican, but 68.0% of office holders 1–2 years after a solar maximum are Democrat. Consequently, Democrats are in the “hot seat” 68% of the time. That is what we are seeing in these data. Solar maxima: 1883, 1894, 1906, 1917, 1928, 1937, 1947, 1958, 1968, 1979, 1989, 2001, 2014. Natural economic contraction points: 1885, 1895, 1906, 1916, 1927, 1937, 1948, 1958, 1969, 1979, 1990, 2001, 2012.
[Sorry, corrected post.] Two unrelated cycles are accidentally somewhat in synchrony: (a) the periodicity of solar maxima, which affect earth’s atmospheric; and (b) the periodicity of natural economic contraction points, which occur every 42 quarters and have a strong impact on the presidential election. Solar maxima naturally occur in spans of about 11 years (averaging 10.9 years between 1880 and 2018), each time causing the atmospheric temperature to rise 1–2 years later before renewed cooling occurs. This is very close to the 10.5-year cycle for natural economic contractions. In the 20th century, both patterns happened to be in pretty good alignment. Whichever party is in office in the wake of a contraction usually loses. Whichever party is in office in the wake of a solar maximum sees the atmospheric temperature rise. In these data, 53.5% of years are Republican, but 68.0% of office holders 1–2 years after a natural contraction point are Democrat. In turn, only 40.9% of years 4–7 years after a solar maximum (i.e., when cooling should be setting in pretty well) are Democrat. So, Democrats get the “hot seat” too many times. That is what I believe we are seeing in these data. Solar maxima: 1883, 1894, 1906, 1917, 1928, 1937, 1947, 1958, 1968, 1979, 1989, 2001, 2014. Natural economic contraction points: 1885, 1895, 1906, 1916, 1927, 1937, 1948, 1958, 1969, 1979, 1990, 2001, 2012.
This sounds very interesting. Sorry I didn’t notice it when it was posted, but I will think about it further before responding. I also improved the formatting in the quote above to encourage others to read it.
2020 update:
https://i.ibb.co/rZmp6rc/temp-By-Pres2020.png
The past data keeps changing for some reason. Eg, for some reason Kennedy now was president during a cooling. This is the data source:
https://data.giss.nasa.gov/gistemp/graphs/graph_data/Global_Mean_Estimates_based_on_Land_and_Ocean_Data/graph.txt
I don’t know what new information could change the temperature estimate from 1960s. But overall we still have net of 1.711 C of warming under democrats and -0.022 C of cooling under republicans.