Joe Simmons writes:
I asked MTurk NFL fans to consider an NFL game in which the favorite was expected to beat the underdog by 7 points in a full-length game. I elicited their beliefs about sample size in a few different ways (materials .pdf; data .xls).
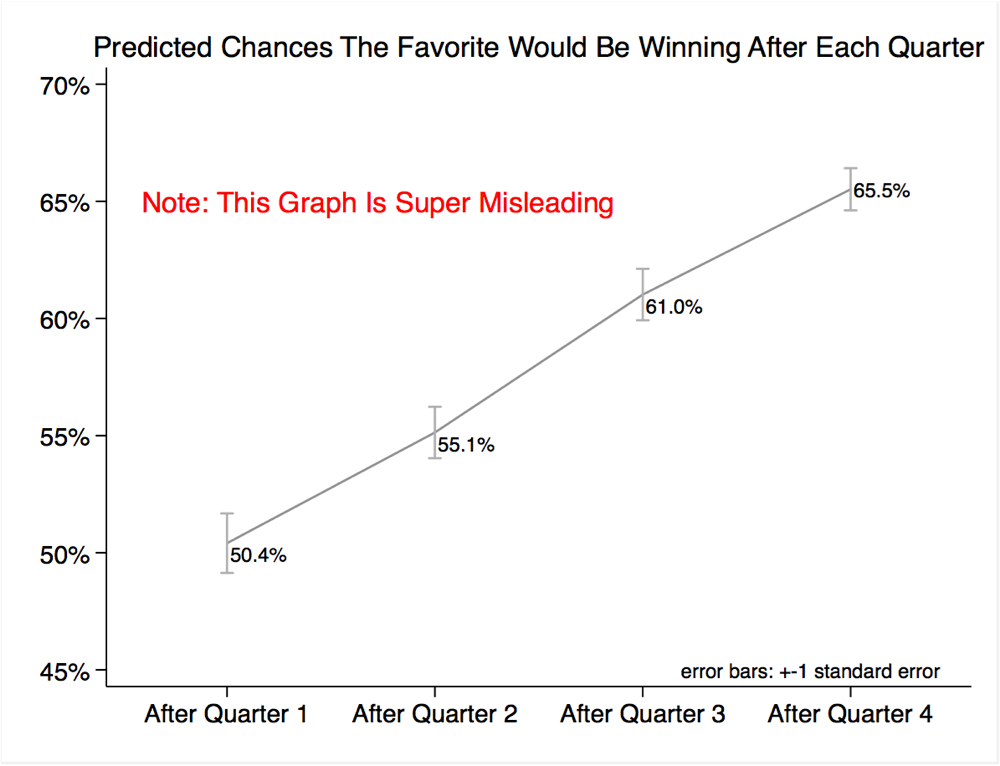
Some were asked to give the probability that the better team would be winning, losing, or tied after 1, 2, 3, and 4 quarters. If you look at the average win probabilities, their judgments look smart.
But this graph is super misleading, because the fact that the average prediction is wise masks the fact that the average person is not. Of the 204 participants sampled, only 26% assigned the favorite a higher probability to win at 4 quarters than at 3 quarters than at 2 quarters than at 1 quarter. About 42% erroneously said, at least once, that the favorite’s chances of winning would be greater for a shorter game than for a longer game.
How good people are at this depends on how you ask the question, but no matter how you ask it they are not very good.
The explicit warning, “This Graph is Super Misleading,” is a great idea.
But don’t stop there! You can do better. The next step is to follow it up with a spaghetti plot showing people’s estimates. If you click through the links, you see there are about 200 respondents, and 200 is a lot to show in a spaghetti plot, but you could handle this by breaking up the people into a bunch of categories (for example, based on age, sex, and football knowledge) thus allowing a grid of smaller graphs, each of which wouldn’t have too many lines.
P.S. Jeff Leek points out that sometimes a spaghetti plot won’t work so well because there are too many lines to plot and all you get is a mess (sort of like the above plate-o-spag image, in fact). He suggests the so-called lasagna plot, which is a sort of heat map, and which seems to have some similarities to Solomon Hsiang’s “watercolor” uncertainty display.
A heat map could be a good idea but let me also remind everyone that there are some solutions to overplotting of the lines in a spaghetti plot, some ways to keep the spaghetti structure while losing some of the messiness. Here are some strategies, in increasing order of complexity:
1. Simply plot narrower lines. Graphics devices have improved, and thin lines can work well.
2. Just plot a random sample of the lines. If you have 100 patients in your study, just plot 20 lines, say.
3. Small multiples: for example, a 2×4 grid broken down by male/female and 4 age categories. Within each sub-plot you don’t have so many lines so less of a problem with overplotting.
4. Alpha-blending.
Or you could try lasagna plots!
http://journals.lww.com/epidem/Fulltext/2010/09000/Lasagna_Plots__A_Saucy_Alternative_to_Spaghetti.15.aspx
Jeff:
That’s a potentially delicious idea. See P.S. added above.
See Figure 3 at http://www.pnas.org/content/110/15/E1398.figures-only for a variant of a lasagna plot with meat.
I don’t like the framing. People could be mislead by considerations like stamina. I’d prefer a strictly random or time invarient process.
PS. How many of those Turkers were Americans?
So you want to show the distribution: Beanplot
http://cran.r-project.org/web/packages/beanplot/index.html
If you have individuals predicting “After Q1”, “After Q2”, etc, the best bet is to fit some simple “model” for each (possibly a line in this case?), to smooth out the noise, then plot those over the beanplot. Possibly also split them into multiple groups so the lines are of 3-4 colors. This chart could be supplemented by panel plots for each individual showing “model” fit vs data.
Did anyone else have trouble figuring out which sheet in that excel file is supposed to be plotted? For some reason I could not understand the description of what is going on here, or else I would try to make a plot to demonstrate what I described above.
I figured it out…Here is an example of the beanplot:
http://s29.postimg.org/785cskd93/footbeans.png
Heavy black line is the average for each quarter, dashed are +/- 1 sd. I don’t think much can be done on the individual level with only four points. The best bet is panel plots.
This bean plot illustrates the quarter-wise marginal distributions better than the original, but seems to be ‘super misleading’ in the same sense as the original: it does not show that majority of the individual predictions are non-increasing over time.
As has been discussed before:
1) Static images on paper are OK, and should be made as good as possible, as per Tufte.
2) But we do live in the 21st century. Smartphones have decent 3D graphics. Starting with an interactive display can often provide viewing superior to any static display, or at least may guide one towards better static displays, especially if backed by link to the interactive.
3) In thsi case, I like the density plot better than the spaghetti graph, but another useful approach is by retired CSIRO scientist Nick Stokes.
See Proxdy plots, one of his many examples.
That one is simple: start with spaghetti plot, rollover label to highlight selected case.
Here’s a more complex case.
One might easily specify subsets to be highlighted, but always in context of all the data, perhaps by graying the others.
John:
I like dynamic graphics that also have clear static snapshots.
Yes, that’s what I was trying to get with ” may guide one towards better static displays, especially if backed by link to the interactive.”
I think the issue is that if one starts with a good interactive, a person can explore and select the most relevant examples. We did this often at SGI.
Across many disciplines, a fundamental principle if good visualizations, especially for big data sets, is:
A) Start with some high-level view in which attributes of interest can be noticed. That may require sliders and controls to select attributes.
B) Allow smoothest zoom-in / drill-down to focus on narrower subsets of data
C) Human visual systems are really quite good, if one can create the right visualizations, which sometimes need creativity or artistry.
D) For a simple example, the UNIX system – I know this “scene in Jurassic Park movie (not in book) used a visualization originall fine as a file system browser, but sometimes used for analysis of sales data.
In general, human beings are poor at thinking about data when presented on paper or on screen. To put it another way, they are poor at generalizing lessons learned using one kind of data to another.
On the other hand, I suspect people are pretty good at getting good at specific analytical tasks. For example, say you regularly take part in a betting game where you can double or nothing, say, after each quarter. My guess is that most people would get pretty decent at this within five or ten games.
What about simply showing 2-dimensional scatterplots of the predictions for each pair of quarters? I think that from these one could see the variation in predictions as well as that many pairs are inconsistent with winning probability increasing over time. One drawback is that this would lose information about, e.g., whether the inconsistent predictions in (Q1,Q2) plot are from the same individuals as inconsistent predictions in (Q2,Q3).
i used to run clustering algorithm (e.g., finite mixture, latent class) on the trajectories, and assign individual trajectory to the highest probable class and plot by class. In this way, we let ‘overlapping’ graphic elements reinforce the class characteristics