Yu Xie thought I’d have something to say about this recent paper, “Evidence on the impact of sustained exposure to air pollution on life expectancy from China’s Huai River policy,” by Yuyu Chen, Avraham Ebenstein, Michael Greenstone, and Hongbin Li, which begins:
This paper’s findings suggest that an arbitrary Chinese policy that greatly increases total suspended particulates (TSPs) air pollution is causing the 500 million residents of Northern China to lose more than 2.5 billion life years of life expectancy. The quasi-experimental empirical approach is based on China’s Huai River policy, which provided free winter heating via the provision of coal for boilers in cities north of the Huai River but denied heat to the south. Using a regression discontinuity design based on distance from the Huai River, we find that ambient concentrations of TSPs are about 184 μg/m3 [95% confidence interval (CI): 61, 307] or 55% higher in the north. Further, the results indicate that life expectancies are about 5.5 y (95% CI: 0.8, 10.2) lower in the north owing to an increased incidence of cardiorespiratory mortality.
Before going on, let me just say that, if you buy this result, you should still be interested in it even if the 95% confidence intervals had happened to include zero. There is an unfortunate convention that “p less than .05” results are publishable while “non-significant” results are not. The life expectancy of 500 million people is important, and I’d say it’s inappropriate to wait on statistical significance to make that judgment.
Getting to the details, though, I’d have to say that I’m far less than 97.5% sure that the effects are in the direction that the authors claim (recall that 97.5% is the posterior probability associated with p=.05 under a flat prior). And, for the usual proper-prior Bayesian reasons, I’d guess that this “2.5 billion years of life expectancy” is an overestimate.
Here’s the key figure from the paper:
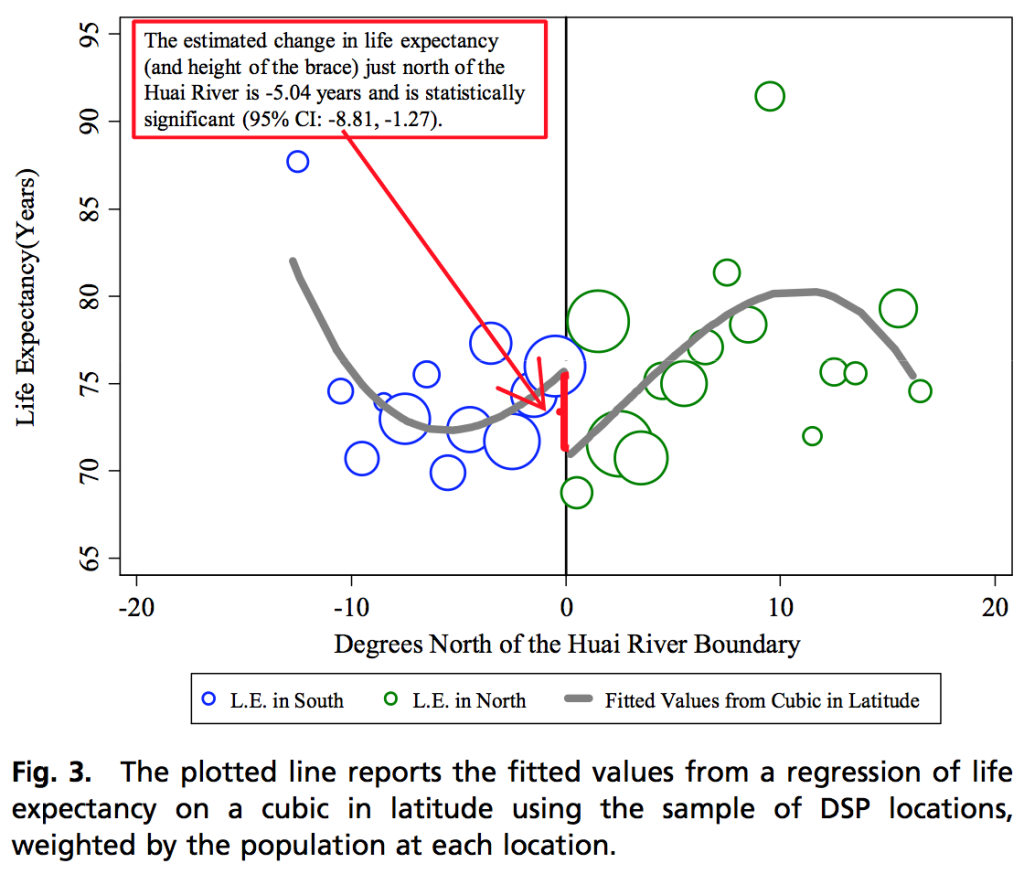
This is a beautiful graph. I love love love a plot that shows the model and the data together. One thing I like about this particular graph is that, just looking at it, you can see how odd the model is. Or, at least, how odd it looks to an outsider. A third-degree polynomial indeed! It looks like that’s where the claim of 5 years of life expectancy came from. I’m a little confused still, because the interval is [1.3, 8.1] in the graph and [0.8, 10.2] in the abstract, so there must be something else going on, but this seems like the basic story.
Table S.9 in the supplemental material gives their results trying other models. The cubic adjustment gave an estimated effect of 5.5 years with standard error 2.4. A linear adjustment gave an estimate of 1.6 years with standard error 1.7. I did some cropping to show you the relevant part of the table:

![]()
My point here is not the the linear model is correct—the authors in fact supply data-based reasons for preferring the cubic—but rather that the headline claim, and its statistical significance, is highly dependent on a model choice that has no particular scientific (as distinguished from data-analytic) basis. Figure 3 above indicates to me that neither the linear nor the cubic nor any other polynomial model is appropriate here; that there are other variables not included in the model that distinguish the circles in the graph. A multilevel model might be a good idea; of course that would increase standard errors in its own way. (Or one could try some less model-based approach such as the robust regression discontinuity method of Calonico, Cattaneo, and Titiunik. I prefer models because, for me, the model-building step meshes with the goal of increasing substantive understanding. But it’s your call. In any case, I’d like to ditch that approach of estimating high-degree polynomials.)
To get back to the main conclusions: There might well be good reasons for expecting an effect of even more than 5 years of life expectancy from this policy—I don’t know anything about this topic—but, from the above data alone, the claim of 5 years looks artifactual. And, there also seems to be an implication that, in those northern areas with life expectancy around 80, that people would be living to 85 in the absence of the policy. Maybe. But it seems like a strong conclusion to make, if it’s being driven by this data analysis alone. Which is what they seem to be doing, in that they’re just taking their estimated regression coefficient and considering it as a treatment effect.
Let me emphasize that I’m not not not saying that particulate matter doesn’t kill, or that this topic shouldn’t be studied, or that these findings shouldn’t be published in a high-profile journal. The accompanying article by C. Arden Pope and Douglas Dockery gives lots of background on why Chen et al.’s conclusions are scientifically plausible.
What I am suggesting is a two-step: the authors retreat from their strongly model-based claim of statistical significance, and the journal accept that non-statistically-significant findings on important topics are still worth publishing.
P.S. This study was featured last month in a New York Times article by Edward Wong. The report was uncritical, referring to “the 5.5-year drop in life expectancy in the north.” Again, I’m not saying the paper’s conclusions are wrong, just that I don’t think they’re supported by the data as unequivocally as one might think from the published confidence intervals.
P.P.S. Let me say all this again because I’ve been posting some negative things lately and my goal is to be constructive, not negative:
Respiration is important. Increasing lifespan is important. There’s lots of evidence that air pollution is bad for you. Policies matter. Environmental policies and environmental outcomes can and should be studied by quantitative researchers. Data are never perfect but we still need to move forward. Subject-matter researchers spend decades of their life establishing subject-matter expertise, and they don’t always have full statistical expertise. That is fine. There is a division of labor. I am a statistics expert and don’t have much subject-matter knowledge about environmental science, even though I publish papers in the area. Regression discontinuity is a great idea. Causal inference from observational data is difficult but still needs to be done. There’s often no easy way to control for background variables in a quasi-experiment. These researchers did the best they could. Their conclusions are consistent with much of the literature and their paper was accepted in a leading scientific journal. Even if their work is imperfect it should not be dismissed. I focus on a statistical concern with this paper because statistics is what I do. I suspect that an improved analysis of these data would yield a higher level of uncertainty, perhaps leading to 95% intervals that contain zero. This would not mean that the true effect is zero, it just means there is some level of uncertainty in the effect given an analysis based only on the data at hand. I am skeptical about an effect of 5 years of life but I could be wrong. I think it would be fine for the journal to publish an article just like this one, but without the 3rd-degree polynomial and with a smaller and non-statistically-significant estimate of the effect. I have the impression that this and other journals have an implicit rule that under normal circumstances they will publish this sort of statistical paper only if it has statistically significant results. That’s a regression discontinuity right there, and researchers in various fields have found evidence that it introduces some endogeneity in the selection variable.
The above post is not an attempt to shoot down the article by Chen et al. I did not read the paper in detail. I’m giving my impressions, and I’m using this example to highlight some general issues that arise with causal inference from observational data, especially in discontinuity designs. (Here’s an earlier example, this time with a fifth-degree polynomial, and on a lighter topic.) I also wouldn’t mind stirring up some post-publication peer review here, and maybe some subject-matter experts can contribute usefully. Again, this is an important topic. Lives are at stake, it’s worth capturing our scientific uncertainty as well as we can here, even if it means that I critique a published paper and possibly embarrass myself in the process.
Get it? Got it. Good.
P.P.P.S. More discussion here.
Haha, I loved that PPS. You should make it a blog post of its own, and then link to it whenever you discuss a paper…
I’d be interested to know if the area south of the river has access to gas or oil-based electricity and heat, or is just burning biomass. If so, there’s no reason to think they are not being exposed to even more dangerous particulate matter and pollutants than is being produced by coal.
The real dangers and harm done by fossil fuels sometimes blinds people to the even worse harm done by the biomass that fossil fuels displace. One of the largest causes of death in many poor countries (an estimated 1-2 million deaths worldwide) is indoor air pollution from burning biomass.
Which is also to say that the absence of a statistically significant association doesn’t necessarily mean that there’s nothing going on– there could be two different effects that more or less cancel each other out, with folks north of the river exposed to more coal pollutants but less particulate matter from burning biomass, etc.
Pingback: TheMoneyIllusion » China life expectancy bleg
“the authors retreat from their strongly model-based claim of statistical significance, and the journal accept that non-statistically-significant findings on important topics are still worth publishing.”
This makes so much sense I don’t see how anyone could object. Having said that, the graph sure does tell a story. A naive look suggests living north of the river, where there’s greater air pollution, increase life expectancy. This is confirmed by the paper which shows the north (bad) side actually has a higher life expectancy than the south (good) side.
They’re only able to reverse that result by using those implausible cubics. Note the two outliers, one on either side with life expectancies above 85 years. Imagine that each of these was shifted north by 8 degrees. This could easily have been the case since in the south, the level of air pollution is roughly constant (according to their data), while in the northern area the air pollution drops off considerably from +10 to +15 degrees. In other words, it’s quite possible given the air pollution data, for those two outliers to have been 8 degrees north of their current positions and still had those same life expectancies.
And yet if you do shift those two outliers 8 degrees north, that would have a dramatic affect on both those cubic curves. On the south side the cubic curve would flatten out into a line, and the one in the north would flatten or possibly reverse concavity.
If small changes which shouldn’t have an effect under the assumed cause, radically change the estimates, then that would seem to be problem.
From a scientific perspective, there is absolutely NO reason to have a discontinuity in the effects unless maybe geographically there’s some high mountain in between that prevents the migration of particulates. Sure, the *policy* has a discontinuity but the particulates don’t. I looked on Google maps and I don’t see evidence of a single high mountain range there. It does look like they have a rapid transition in the particulate concentration near the boundary (their graph fig 2) but I’d say the discontinuity overshoots, something like a spline would work fine, I’d probably use a 2D gaussian process myself.
Second, it’s not clear to me that they used *orthogonal* polynomials, and if the polynomials are not orthogonal to the offset, then the offset coefficient isn’t an indicator of the average difference. I’m not sure if that affected them here or not.
It doesn’t seem to me that with a physical atmospheric pollutant the “regression discontinuity” design does anything like what they claim it does: “The RD design was developed more than five decades ago and has been used successfully to test the causal nature of relationships in a wide range of fields”. Sure in a wide range of fields, but not obviously in this case.
I can’t find where they report results from equation 1, a simple model involving TSP (total suspended particulates), which *already* varies by geographic region due to the policy. The supplement seems to refer to OLS and “two stage” but I am not sure if that means (equation 1 and equation 2abc or not, since they’re fitting both of these by OLS) and it doesn’t have consistent terminology with the text of the paper (for example I can’t just find a table or graph where they show Beta_1).
How I would tend to want to build this model:
1) Build an exposure model: using monitoring data and a gaussian process prior build a 2D function that measures exposure to TSP regionally. Preferably a timeseries of this function with at least an average over quarters of the year (seasons).
2) Build a causal model: based on measured covariates such as smoking, diet, climate, and the imputed exposure, estimate a mortality rate curve by age. To figure out how exposure determines mortality, use a nonlinear relationship between exposure level and mortality rate, and put a gaussian process prior on this nonlinear relationship, include climate in the mortality rate data, I believe that high heat + high particulates is probably worse for your health than cold + particulates but the actual subject matter experts should probably already have some information about particulates + weather. Estimate this model for overall mortality, and respiratory mortality.
3) With this design, the important parameter is the mortality rate vs TSP + weather + age curve. You can show a spaghetti plot and confidence bands of mortality rate vs age for typical conditions in say 4 quarters of the year (a 4 panel plot).
4) To actually see the effect of the policy, you’d have to have a counterfactual estimate: what would mortality look like if they stopped giving out coal? Run the fitted model forward through a year but with TSP levels reduced by various amounts, provide a graph that shows overall or respiratory mortality in each counterfactual TSP reduction condition. Have one endpoint be the “current” level, and one endpoint be the level “well south of the border” and say 3 levels in between.
Obviously I’d be tempted to fit all this in Stan!
Also I should say measure quality adjusted life years lost, it makes a BIG difference in my opinion if 0-3 year old are dying because of high sensitivity to particulate pollution vs if 80 year olds are dying 3 years earlier….
Mean life expectancies are much more sensible to increases in mortality at young age than at old age, due to design. That has nothing to do with QALYs.
Something else: if we are to believe an effect of ~5 years, shouldn’t the life expectancy of the topmost green circle increase to 97-98 years? Is that realistic?
If you mean that the “quality adjusted” part isn’t so important, then ok, it’s a second-order issue I guess. The point is if you keep a child from dying in its first 3 years, it will live to be on average maybe 75 or 80 so you’ve saved 70+ years of life, the best you can do for someone who starts out 75 yo is add far less than an additional 70 years.
The quality adjusted part would come about because if you live to 75 but have terrible asthma from birth and are constantly getting bronchitis and things that’s also a serious concern.
Daniel,
I think you are being a little unfair, but maybe I’m just being all defensive applied micro guy. And I think I can frame this in a way that might make you more sympathetic, so let me try. I actually think that the 2-step bit is the real core of the paper. And I think the reasoning is very sound quasi-empirical reasoning. It’s basically a formula for how you do these things in applied micro, and it goes like this.
1 – Show the “reduced-form” effect of the boundary on the outcome of interest. That’s the graph Andrew posted, and it shows (whether you believe the cubics or not) that there seems to be some difference between N/S in life expectancy that appears discontinuous at the river.
2 – Show that your “policy” directly affects the hypothesized causal route. That is in Figure 2 – If you don’t see a discontinuity there, I don’t know what to say. But it seems pretty clear that the effect of the policy in the world is a difference in pollution on either side of the river, even if pollution blows around in the wind. This is the “first-stage” of the 2-step – it is a graphical version of the first stage in an instrumental variables procedure. It shows you that policy –> effect on pollution.
3 – Do the IV – instrument pollution with distance N/S of river, predicting pollution for each city. Then regress mortality on predicted pollution. This scales up the reduced-form results from (1) and gives you the right units.
It all seems rather convincing to me, but then again, this is the kind of stuff I like.
As for the model specification, it is odd to me they use a polynomial. I was under the impression that using a a kernel-weighted local regression was the most common thing here, so basically you’d just be tracing out the local mean either side of the cutoff using the neighboring observations. But the whole point of the model here is simply to predict the cutoff on either side. I don’t think there is a good argument that the linear form is the obviously best. Like I said, I prefer the local kernel-weighted regression, but I would bet it doesn’t change the story much.
FYI – the OLS results are in Table 2 on page 5 I think.
quick response since I’m super busy at moment:
I took this (based on the title) to be a paper trying to do some combination of epidemiology and environmental engineering but using some kind of econometric techniques. If they’re really trying to claim that the policy of giving away coal is the key and not the exposure to particulates, then they should have written a different paper (or certainly a different title).
In the context of a causal (exposure -> health outcome) model they need to deal with the 2D nature of pollution (really 3D but 2D is enough since the monitor stations are at ground level) instead they’re doing just a 1D model plus some kind of correction for nearness to the coast.
The fact that their straightforward model involving TSP maybe doesn’t show the effect they’re looking for unless they account for the regression discontinuity is actually evidence that it *isn’t* TSP exposure that causes any affect, since the thing that the regression discontinuity is most strongly indicative of is the economic difference (ie. the equivalent income of the coal they get free maybe).
I’m not saying they aren’t on to something, but it seems like they need to tease it out more rather than just pointing a well understood econometric technique at this data.
Maybe I can respond in more detail tomorrow.
1) I don’t think their graph shows a discontinuity in life expectancy at the boundary. It shows that *when you model the variation as two cubics* the two cubics are different. But that seems to be overfitting. I’d love to see a loess through the raw data. The noise in the life expectancy vs northiness data is substantial and undoubtedly has something to do with collapsing a really broad circular region into a line
(here’s the region: https://www.google.com/maps/preview#!q=Huaihe+River&data=!1m4!1m3!1d4057332!2d117.5216743!3d31.5516393!4m10!1m9!4m8!1m3!1d479969!2d119.66802!3d36.2475262!3m2!1i1610!2i895!4f13.1 )
2) The policy certainly seems to affect the air quality, Figure 2 does have a change. I wouldn’t call it a discontinuity, the discontinuity model over-predicts pollution in the points just north of the river for example. Let’s call it a region of rapid change.
3) They don’t need to “predict” pollution, since they have it measured, and they have it measured in relatively better 2D detail. Apparently, that model where they simply regress on pollution and confounding factors doesn’t show a very strong trend, their coefficient is 0.04 +- 0.02 on cardiorespiratory disease. Or -0.52 years of life expectancy overall.
They see a bigger difference if they a) add in a discontinuity which is policy related, not exposure related (the variation in exposure is *already* in the TSP data) and b) use an implausible cubic regression, which also is a sort of researcher degree of freedom (though they report the linear fit too, they emphasize their cubic).
It seems to me that if they believe that exposure produces health outcomes, then they should do a good job of interpolating exposure, and show that the exposure has health effects by directly estimating the effect of exposure on mortality and morbidity rates by age.
With a different version of their analysis, and a different hypothesis, I could easily imagine getting a result where they find that giving out free coal improves the life expectancy of people in the northern region, as Entsophy points out except for two big outliers there appears to be an upward trend in expectancy vs northiness.
I think the idea of looking at coal burning, and air pollution on life expectancy is a great idea, and that this region is a perfect area for study, but their analysis is not very convincing. I wonder if they have a dataset available?
My approach to looking at material like this is to get into the data itself, meaning the supplements (if the data is there at all). The list of adjustments they made is interesting – including a “coastal adjustment” – and they seem to have done a nice job identifying potential problems like people dying in a place other than where they lived. I like to see raw data and then how it’s been processed. This is not exactly what I like but it’s interesting to look at the S1 table and see a difference in heart disease deaths, stroke deaths and respiratory illness deaths. Two of those lean to one side – to the North. If I were guessing, I’d think likely respiratory illness and maybe heart disease would lean to the North. But that isn’t true; respiratory illness mortality is shown as higher South. That makes me go “huh?” It’s a frustration of my prior. I didn’t see discussion of this. It kind of freaks me out: if this study is about inhaled stuff, then why do I see that number?
Only after I have a handle on the data do I think about the part of the work which generates a result. This stuff is so complicated with so many correlations and balled together causation that each view is, to me, just that: one view of many.
As a user of regression discontinuity, I applaud their attempt to use it in this context. Something that could have dulled these critiques about modelling would have been using the same methodology on another boundary (maybe a another river) where they didn’t expect a discontinuity and see if they found similar results.
Another, possibly bigger problem, is that the policy that provides their discontinuity likely has many more effects than simply changing air quality (if, as a previous commenter mentioned, it even does that). What if people with access to the program spend their new found disposable income (the money they previously spent on coal) on alcohol or on health care? Many things are likely changing discontinuously at the cutoff, not just air quality.
Lastly, RD gives a local average treatment effect. In order to get their 2.5 billion life years they must assume geographic homogeneity. Not working in this area myself, I can come up with plausible-sounding reasons why this wouldn’t be the case. Maybe people living further north spend more time indoors so the effect may be even larger there. If they wanted to present this number, maaaybe in the discussion, but not as the first line of the abstract.
Probably a naive question: If I drew arbitrary vertical lines on the graph above that Andrew posted, and fit cubics to points on either side, would the cubics be close to continuous across my artificial discontinuities? Just wondering.
Suppose that the discontinuity they say is there is real. First you’d want to remove it. Then I think you could do your test. Problem is, it’s not just that jump they’re claiming is there, the shape of the two cubics is entirely different isn’t it?
I don’t get what you mean by the shape of the cubic: e.g. if I translated down the left cubic till they both matched on that discontinuity, they seem to smoothly blend to the eye? Or not?
My point was that taken essentially smooth data where one doesn’t suspect a discontinuity a priori (e.g. smog data of the US states, or even the data in this example restricted to any one side of the river) even for such data, if we arbitrarily fit a line piece-wise on either side of an arbitrary limit ( or worse a high order curve or spline) unless you add an external fitting constraint for continuity or differentiability will such fitting curves coincide at any arbitrary dividing line? (My gut feeling says they won’t)
If they won’t, why isn’t this mismatch just another artifact? Especially given the researcher degree of freedom in choosing the sort of curve you want to fit with.
I agree, with pretty much any data, if you give a fitting procedure an extra degree of freedom, it will rarely decide to set that degree of freedom to almost exactly zero (without some extremely strong prior put on it for example).
What I meant about the shape is that it’s not clear to me from their description if they’re just offsetting each side or if they fit different coefficients on each side. Ie. did they fit the model
y = a_i + b_i x + c_i x^2 + d_i x^3
where i is either 0 (on the left) or 1 (on the right) so that the two cubics are allowed to be completely different
or did they fit
y = a + aa (north = true) + b x + c x^2 + d x^3
where north=true is 1 or 0
If they just fit a constant offset (the second model) it’s not clear why they think that makes any sense.
The life expectancy of 500 million people is important, and I’d say it’s inappropriate to wait on statistical significance to make that judgment.
Whoa there with the appeals to emotion. The reason for the significance test is that so many findings turn out to be wrong even with the test. Mistakes that affect 500M people are very big problems, just ask Mao about his plan for a billion peasants to make iron in their fireplaces at home.
The reason for the significance test is that so many findings turn out to be wrong even with the test.
The unintentional comedy in a statement like this being directed at Andrew is priceless.
+ 1
Pingback: Regression discontinuity with wacky high-order polynomial correction | Symposium Magazine
Huai River only divides eastern china into north and south. Within the similar latitude, there is a mountain range that cuts the west side. People on the south side do use portable electric heater since 90s.
I agree that ‘there are other variables not included in the model’, and I think it is better to take care of them in the experimental design stage rather than to model these relationships, if the purpose is to assess the impact of a policy. I would think studies with human (or non-human) samples collected closed to the river (i.e., like those circles in the plot with x coordinates close to zero) have less internal variation, assuming there is less social/economical difference. With non-human subjects, we can even randomly assign them to different locations.
In designing these experiments, I guess no researcher would be really comfortable to power the study based upon an effect of 5 and sd around 2.
I think journals should push for a requirement of p-value less than 0.05 from studies specifically designed to test the hypothesis, rather than mining convenient samples with ‘optimized’ analysis technique, which is a useful and indispensable tool to generate hypotheses (rather than formal testing).
Remove the model lines from the paper’s Fig 3, and change the color so that all the data circles are black. Now find – from the data, not using the x-axis values – where the river is. Just by eyeball, you can’t. Yes, eyeballs aren’t as good as numerical analysis in some cases. But here they are illuminating. If I can’t see an effect in the graph, then I expect any effect to be so small it may not matter.
In this decolored case, I’d say there *may* be a slight upward tilt to the right, and apparently two outliers, one north and one south. With all the scatter, I doubt it’s worth modeling with anything more complex than a straight line.
The slight upward tilt would be in line with the hypothesis. But it’s pretty weak support.
> Remove the model lines from the paper’s Fig 3, and change the color so that all the data circles are black. Now find – from the data, not using the x-axis values – where the river is. Just by eyeball, you can’t.
I can’t. They should have applied that reality check to their conclusions. In general, conclusions unsupported by the eyeball test should be regarded with skepticism.
Has anybody ever estimated the change in average lifespan in Southern California due to the spectacular reduction in smog in recent decades?
I’m enjoying the smog reduction, but I think the timeperiod of 1980 to now saw a lot of changes in many variables other than pollution (for example smoking, exercise, diet, car safety standards etc). And US residents already had fairly high life expectancy, I imagine seeing this effect in life expectancy data would be hard. On the other hand, I bet it would be easy to see in some kind of quality of life data, asthma rates, number of “stay indoors” alerts per year, bronchitis rates, etc etc.
Daniel,
I’ll get to your big (and good) response to me above this afternoon if possible, but since here we are talking about SoCal and smog reduction, wanted to make a quick point. Much of this work uses policy as “plausibly exogenous” variation in pollution levels (as in this China paper). The reason this is used, instead of the pure particulate rate, is over a concern about sorting/selection-into-treatment. This is almost the paramount concern for micro-econometricians – who was “treated”, and why were they “treated” and other people not.
In the case of CA or China, you might think that people with relatively high preferences for health (conditional on observables) would move away from smoggy/polluted areas. They would be exposed to less pollution and have better health outcomes, but that wouldn’t be a causal effect of the pollution (it would in part be an effect of sorting/selecting-into-location).
If a policy comes along and changes pollution levels from the outside, that negates the selection problem (at least in the short term – at least that is the logic). That is why they don’t want to use direct pollution rates in their estimates, but want some “instrument” that moves pollution levels for people in some places and not others. So, in theory (whether you believe it or not), using variation in pollution caused by a policy change will allow you to ignore some of those confounding variables you’ve listed (smoking rates, diet, car safety) and get just the pollution effect out of your estimation. This is basically the entire premise of reduced-form microeconomics.
I get it that you’d like to avoid self-selection into categories, but I find it hard to believe that this analysis does anything like that.
1) they’re not talking about a sudden 6 month policy, they’re talking about a policy initiated in 1950 that ran until 1980 and then the impact of the home heating furnaces remains since they haven’t all been replaced. All the assortment possibilities work against their model, by now everyone has equilibriated to their preference for more or less smog vs. whatever other tradeoffs there are.
2) Since it’s hard to even know the sign of the assortment effect ahead of time, you’re stuck analyzing covariates like smoking and weather and etc. Did assortment effect mean that people with chronic pulmonary problems have largely moved south, or that people with a lot of health concerns moved south? Both but to different extents? I understand that if this policy went into place *last year* you’d be all set to see what the before-after effect was, like in some of the smoking ban studies.
3) Analyzing by age as I suggested is even better, few babies have much say in where they live, though of course parents may be likely to move away from polluted areas when they first have children I suppose.
Yep – well, at least a little bit, mostly using the Clean Air Act (another policy instrument) and the fact that parts of that applied only to counties above a certain pollution threshold. So they look at changes in health outcomes in counties that came under increased regulation compared to those that didn’t. I don’t know of CA specific studies, but I think there are probably some.
It was actually the same guy, so go to Michael Greenstone’s page and you’ll see all his work on this (in particular, the stuff with Ken Chay).
Those reductions in emission levels are much smaller than some of the reductions we’ve seen in China, and some people say that the smaller estimated effects from that work are likely due to some non-linearity in the effect of pollution on health – really high levels are terrible, moderate levels are just sorta bad.
There are some smaller, better identified studies too (they put ozone sensors in farms and followed agricultural worker productivity in one case – big effect), but the published work from the Clean Air Act all seems fairly consistent in finding smallish but meaningful effects on own health (and the health of babies).
Thanks. I focus on Southern California because I grew up here, but also because the environmental policies have been extraordinarily successful. But they’ve also been extraordinarily costly — my back of an envelope calculation of the national expenditures so far in terms of reduced gas mileage to lower smog mostly in LA, Albuquerque, Denver and few other mountain valley metros is closer to a trillion than a billion dollars.
Get it? Got it. Good.
http://www.youtube.com/watch?v=KM1VXhZT37E
Pingback: Links for 08-07-2013 | Symposium Magazine
A few quick comments:
1. One of their hypotheses should have been whether there is a changepoint at zero. (One paper which takes a Bayesian approach to changepoint detection here – http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.39.4002&rep=rep1&type=pdf.)
2. Need to see confidence intervals associated with polynomial fits and – more significantly – how the polynomials extrapolate beyond the data range. Need to do that to assess limits of interpretation of the fit results.
3. Why a polynomial fit? Why not LOWESS/RLOWESS? In the absence of a model which suggests a polynomial is what you should choose, LOWESS would seem to provide more flexibility in adapting to the data.
4. Whether you do a polynomial fit, LOWESS, or something else bootstrap to determine the best fit and associated confidence limits.
Pingback: Journal Refereeing Practices and Polynomial Regression: Threat or Menace?
Pingback: Links 8/11/13 | Mike the Mad Biologist
Pingback: Somewhere else, part 68 | Freakonometrics