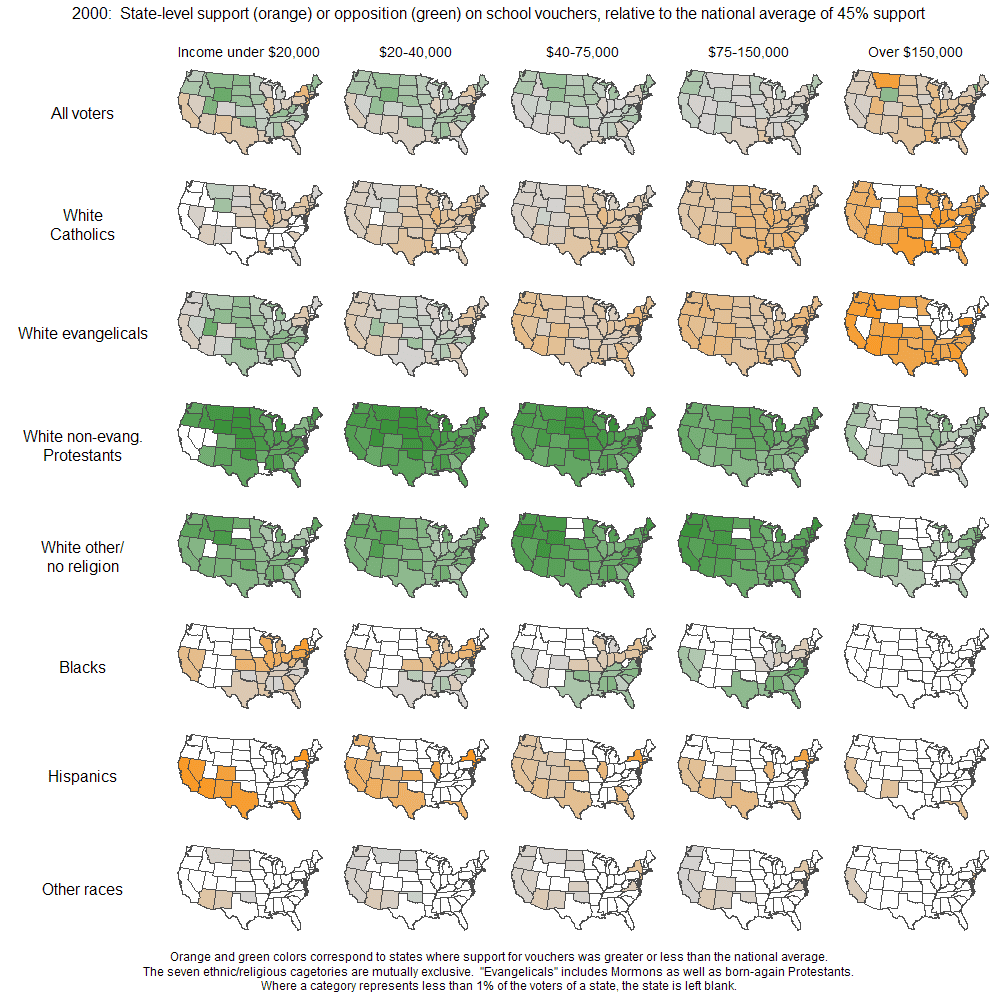
Here’s our estimate of public support for vouchers, broken down by religion/ethnicity, income, and state:
(Click on image to see larger version.)
We’re mapping estimates from a hierarchical Bayes model fit to data from the 2000 Annenberg survey (approximately 50,000 respondents).
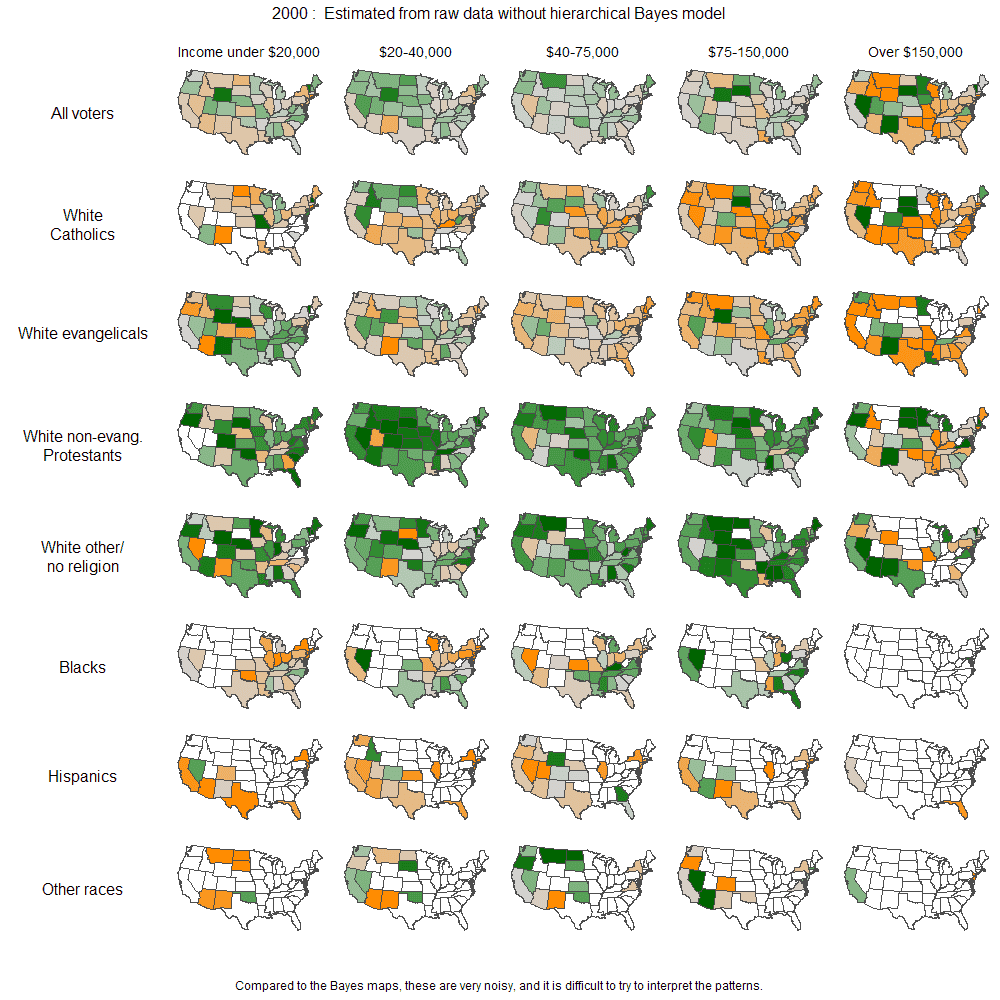
In case you’re wondering what Bayesian modeling did for us, here are the corresponding maps from the raw data (weighted to adjust for voter turnout, but that doesn’t actually do that much anyway):
(Click on image to see larger version.)
OK, so Bayes gives you a lot. The costs?
– Effort. It took me a couple weeks to make the first set of maps. Some of this was the modeling–I tried several different versions of the model and also had to come up with a quick-and-dirty way of adjusting for the turnout weights amid the regression modeling and poststratification.
(I also put in a lot of work to make the maps look just right, but it’s not really fair to count this as a cost: if we were only able to look at the raw data, we wouldn’t even be trying to make such maps in the first place.)
– Model dependence. Changing the model will change the estimates and change the maps. I don’t feel so bad about this, first because the raw estimates are so noisy, second because so-called raw estimates are themselves highly model dependent.
Everything depends on models, so let’s take them seriously
This discussion relates to my disagreement with Kos over the maps of Obama and McCain vote. I graphed model-based estimates constructed using the Pew pre-election polls; Kos didn’t trust these where they disagreed with published exit poll results.
The problems with Kos’s argument?
1. Exit polls are far from perfect: I’ve heard that in 2008 the raw exit poll data weren’t close to the actual election outcome.
2. Exit poll estimates depend strongly on the model used to select polling locations, assumptions about who responds to the poll, and the models used to adjust for sampling error, nonresponse, and unexpected contingencies.
P.S. I expect that other, non-Bayesian methods could also work well, and I’d love to see how they do on this and similar examples. As we always say, what’s important isn’t the method, it’s the information included in the estimate. A strength of Bayesian hierarchical modeling is that it allows inclusion of diverse sources of information, but I’m sure other methods could do fine also, if set up appropriately.
P.P.S. Lots of comments below on the map colors. I appreciate these suggestions, but please recall the main point of this entry, which is the impressive ability of Bayesian data analysis to give reasonable estimates for all these subgroups.
wouldn't the colors make more sense if they were flipped? green seems to say "go" to me, ie, be the positive choice (support).
also, can you explain what the model has done to change Utah from being so supportive in the raw data, but very un-supportive in the model (for white non-evangelical 20-40k)? is the idea that the sampled people/opinions were not representative of the actual population, so your prior distributions adjust for this?
I chose the colors as follows: Vouchers are generally supported by Republicans (hence orange color, which is close to red) and opposed by Democrats (hence green, which is close to blue).
Regarding Utah, I'm guessing the model is just doing some smoothing given the small sample size. However, it could be a coding error. I threw Mormons into the "evangelicals" category (see the notes at the bottom of the top graph), and it's possible that I messed something up when doing that. I'll check.
I'd suggest using other color pairs. Red/green is bad because of the prevalence of red-green color-blindness (7% of males according to the Wikipedia article).
Is there some reason there's no key relating percent support to color intensity?
Hi, Bob. I see your point on the colors. At the very least we could have an alternative for colorblind people. I'm not quite sure what to use, though. Maybe red/blue, but perhaps that's confusing because it would seem too closely tied to partisanship.
Also, I have mixed feelings about a key to the colors; I fear that it encourages the reader to a pointless game of going back and forth between the map and the key, essentially using the map as a look-up table. For a look-up table, I prefer parallel coordinate plots, which in fact I also did for this example. A compromise would be to give the numerical estimates for a few states (for example, New York and Texas), which would help people get a sense of the scale of the colors. For my main point here (advertising Bayes), I didn't think this was really necessary.
P.S. I looked at Utah more carefully. Sample size is small there, so the Bayes estimate is borrowing heavily from the model.
Some papers about colours in graphical displays:
by Ross Ihaka
http://www.ci.tuwien.ac.at/Conferences/DSC-2003/P…
by Achim Zeileis
<a href="http://statmath.wu.ac.at/~zeileis/papers/Zeileis+Hornik+Murrell-2009.pdf" rel="nofollow"> <a href="http://;http://statmath.wu.ac.at/~zeileis/papers/Zeileis+Hornik+Murrell-2009.pdf” target=”_blank”>;http://statmath.wu.ac.at/~zeileis/papers/Zeileis+Hornik+Murrell-2009.pdf
by Thomas Lumley
<a href="http://stat-computing.org/newsletter/issues/scgn-17-2.pdf" rel="nofollow"> <a href="http://;http://stat-computing.org/newsletter/issues/scgn-17-2.pdf” target=”_blank”>;http://stat-computing.org/newsletter/issues/scgn-17-2.pdf
I asked my brother to look at the chart. He couldn't reliably make out the color differences so it is a concern for the large number of males who are red-green color blind.
Color Universal Design (CUD)
– How to make figures and presentations that are friendly to Colorblind people
http://jfly.iam.u-tokyo.ac.jp/color/
Sorry, but I also think the color choice is awful. You are representing 2 extremes (above the national average, below the national average) on a continuous scale and thus your colors should represent that. Green and Orange are not intuitive opposites (ie like white and black) and there is no intuitive middle ground (ie gray). If you use intuitive opposing colors you don't need a color ramp (but you should have one anyway). As it is I had to spend about a minute squinting back and forth at the caption and the maps. If you presented these graphs in a geog department, you'd get reamed on the color choice and no one would focus on the results. Check out the color brewer http://colorbrewer2.org/ or get a basic intro-cartography book. I like 'Making Maps' by Krygier and Wood.
I threw together a clickable swapping version from these images. http://anyall.org/gelman_bayes_maps
View your web page as it will be seen by someone with any of a variety of kinds of color blindness:
http://colorfilter.wickline.org/
That page includes among much useful information this link for selecting safe colors:
http://colorlab.wickline.org/colorblind/colorlab/