Alex Tabarrok writes:
Here’s a regression puzzle courtesy of Advanced NFL Stats from a few years ago and pointed to recently by Holden Karnofsky from his interesting new blog, ColdTakes. The nominal issue is how to figure our whether Aaron Rodgers is underpaid or overpaid given data on salaries and expected points added per game. Assume that these are the right stats and correctly calculated. The real issue is which is the best graph to answer this question:
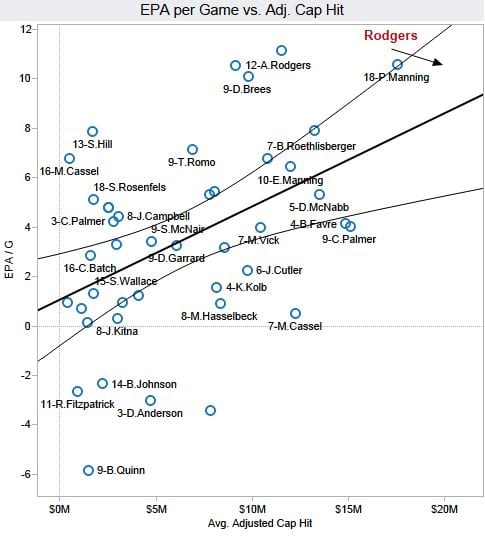
Brian 1: …just look at this super scatterplot I made of all veteran/free-agent QBs. The chart plots Expected Points Added (EPA) per Game versus adjusted salary cap hit. Both measures are averaged over the veteran periods of each player’s contracts. I added an Ordinary Least Squares (OLS) best-fit regression line to illustrate my point (r=0.46, p=0.002).
Rodgers’ production, measured by his career average Expected Points Added (EPA) per game is far higher than the trend line says would be worth his $21M/yr cost. The vertical distance between his new contract numbers, $21M/yr and about 11 EPA/G illustrates the surplus performance the Packers will likely get from Rodgers.
According to this analysis, Rodgers would be worth something like $25M or more per season. If we extend his 11 EPA/G number horizontally to the right, it would intercept the trend line at $25M. He’s literally off the chart.
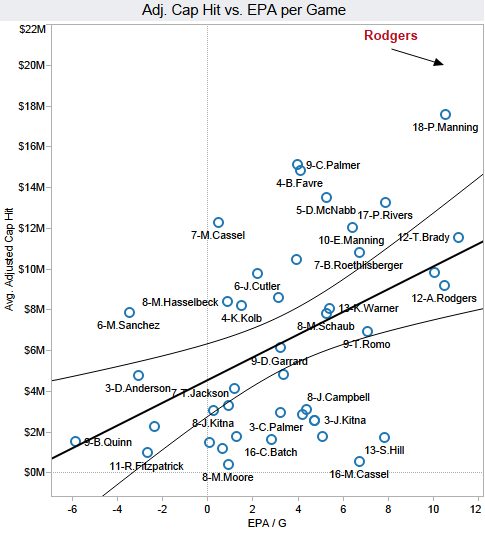
Brian 2: Brian, you ignorant slut. Aaron Rodgers can’t possibly be worth that much money….I’ve made my own scatterplot and regression. Using the exact same methodology and exact same data, I’ve plotted average adjusted cap hit versus EPA/G. The only difference from your chart above is that I swapped the vertical and horizontal axes. Even the correlation and significance are exactly the same.
As you can see, you idiot, Rodgers’ new contract is about twice as expensive as it should be. The value of an 11 EPA/yr QB should be about $10M.
Alex concludes with a challenge:
Ok, so which is the best graph for answering this question? Show your work. Bonus points: What is the other graph useful for?
I followed all the links and read all the comments and I have my answer, which is different (although not completely unrelated to) what other people are saying. It’s interesting to see people struggling to work this one out.
But giving my solution right now would be boring, right? So I’ll leave it up for youall to discuss in comments, then in a day or two I’ll post my answer. I will say this, though: it’s not a trick, and I’m not trying to use any football-specific or NFL-specific knowledge.
Enjoy. I’m teaching applied regression and causal inference this fall and spring so it’s great to have examples like this. Although maybe this one’s a bit too complicated for an intro class . . .
P.S. I’d prefer the graphs to just have the names and get rid of those distracting little circles all over the place.
If you got rid of the circles you’d probably want to center the names on the datapoint, and this could lead to collisions, no? Look at Carson Palmer’s position on both graphs. He’s to the left and to the right of his circle rather than centered underneath as most of the names are.
Dmitri:
Sure, some of the names might have to be jittered a bit, but I don’t think that’s a big deal in this case.
I agree with you about the substance, but I think people rightly have a fear of tinkering with the data for merely cosmetic reasons. I know that I would like my graphs to rigorously reflect what’s in my dataset, even if a little tinkering wouldn’t hurt anyone. I’d like them to be able to estimate the numerical quantities based on the graph. Plus I don’t want to get into arguments about how I’m putting my finger on the scale, etc.
I say all that while agreeing with you that in this context it wouldn’t really matter.
It’s easy to find out what a 11 EPA/G quarterback is worth. There are four of them in the data set. The pay levels are: 9, 10, 12, and 18. The regression is just adding noise by giving information about other kinds of quarterback who are not relevant given that I have a decent size sample of truly comparable observations. The answer is that using a regression is a dumb way of getting the answer to the question, or alternatively stated it’s a dumb model, which badly predicts pay for the kind of player we are interested in.
You say it’s easy to determine what an 11 EPA/G quarterback is worth and then provide 4 numbers that are drastically different?
Same problem here: https://fivethirtyeight.com/features/billion-dollar-billy-beane/
I teach this example in my class at Penn. The hint I give is to remove from the data the player in question and consider two hypothetical worlds; in one, the relationship between salary and performance is linear with r close to one and the other where the relationship is r close to 0. Now value the player who is far off the line under each scenario.
Adi:
I read the linked article, and it’s fun, but I don’t quite buy their reasoning, as it’s not clear that whatever Beane did in Oakland would transfer to Boston. I mean, yeah, sure, you gotta believe that as a good GM he could win some games, but my instinct would be to regress this toward the mean a bit.
I agree that considering the special cases of r = 1 and r = 0 can be helpful.
They did regress the estimate towards the mean by a whole lot: towards the end, they assume Beane could have gotten Oakland-like performance with an Oakland-like payroll, but that to go beyond that he would have had to pay the same extra amount per win that applies (on average) in the league as a whole. That could still overestimate his impact, of course — for instance, maybe the nonlinearities in player pricing are such that there are fantastic bargains to be found just below the top players, but the very top the players are fairly valued. But it’s not like the analysis just assumes Beane could get the same number of victories per dollar that he gets in Oakland.
OK, I’ll have to read it more carefully, then!
I prefer the second one. One of the golden rules of regression analysis is …’ do not extend your model beyond the range of the observed X values (or at least do it very cautiously)’ and the first graph contradicts this rule because there aren’t other players paid > 20m. In the second graph the point under investigation is still quite extreme and therefore the uncertainty is large but at least there are some points with EPA/G close to 11
Isn’t the real question whether to use Y(X) or X(Y)? In this case, it says to assume things are measured correctly – a big assumption, considering that one of the variables is expected points added per game (which would seem to be subject to measurement error). But, if we do assume that, then I think the question concerns how salary depends on that measure, which would lead me to the second graph. If we start thinking about the measurement errors, I think orthogonal regression might be a better approach. In any case, I don’t like either linear fit much – I would really want to add more factors, using the second graph as a starting point. I think of the 4 data points with EPA/G = 11, as an extreme case of that approach – if we can’t identify these other factors, then only focus on the data points close to the one of interest. However, that usually results in a very wide range of estimates, given the small number of data points.
> If we start thinking about the measurement errors
Maybe the story of the two plots coming from leverage? The data itself looks like a bubble and the most extreme points in $ are kinda different than the most extreme points in EPA/G, and so you get a different story.
I don’t really like either plot in the context of the decision cause I don’t think they’re really telling us anything (even if we assume the EPA/G and $ numbers are perfectly accurate). We’re not picking between all the different points here. If we could just stick with cheap Aaron Rodgers, or Tom Brady, or Drew Brees, then we would.
> then only focus on the data points close to the one of interest.
I think if I were in the position I would do something like this. I guess the limit of this isn’t gonna work (cause who’s more like Aaron Rodgers than Aaron Rodgers? — that should be a very compelling argument for no pay raise!)
I’m mildly confused by what the adjusted cap is. Maybe it is also a complex thing. I went to the Drew Brees Wikipedia page and got “On July 13 [2012], the Saints and Brees agreed to a five-year, $100 million contract.” — so where did the lowball Drew Brees number come from (this article is 2013)? Also some of the circles don’t have names in both plots :/, so it’s nice they’re there.
I’ll bite. These OLS trend lines both assume error in y and no error in x. The premise of the question is that the player has some true value to a team measured in dollars. By asking whether Rodgers is over- or under-paid the question necessitates that we view the actual salary as a noisy measure of this value. So to me the first regression cannot plausibly answer the question at hand. If I literally knew nothing about football, then my answer would end here. But knowing a tiny bit about football, I can add that expected added points per game (EAPPG) is also surely a noisy measure of this value, and even more so because its predictive performance for future EAPPG is probably imperfect (perhaps with some regression to the mean). Writing down the appropriate measurement error model with at least a weakly regularizing prior on the true latent values would be my approach to an answer.
I’ll also add that my prior is that teams are pretty savvy in figuring out what players are worth, and in general I trust the value of a new contract to be a better estimate of a player’s value to the team than a single measure of performance. So my prior here is that he’s paid about right.
There’s information in the data about how much $ somebody with Rodgers’ EPA should be making, because there are other players with comparable EPA’s (Manning, Brady, other Rodgers). But there’s less information in the data wrt how many points someone making Rodgers’ salary should be scoring, w/ only Manning contributing to the estimate locally, so the model is comparably less sure what values are appropriate there.
There’s also still a lot of residual uncertainty in scatterplot, so showing predictive intervals would probably be better than the OLS estimate +/- 1SE or whatever that is. It also feels like $ should be on a log scale — would probably help with heteroskedasticity (specifically, lower paid athletes being less free to vary in pay vs higher paid athletes on the raw scale), and also squares better with my (admittedly impoverished) sports intuition (since sports are winner-takes-all, I wouldn’t expend linear trends in raw compensation vs. performance — if everyone’s equally competent, you’d be willing to pay a lot more for a small increase in performance, since your probability of winning probability of winning would scale weirdly with player ability)
It also seems like “being on the team” or “in the NFL” or w/e might be serving as a collider here — it might be that players comparably compensated might not be as good at getting those direct expected points but are good at helping others get them, or something.
Regressing Y on X or X on Y? this is the problem!
This article has a simple answer for a case that direction of dependence between skewed variables is unknown https://www.jstor.org/stable/2685529
https://ocw.mit.edu/courses/economics/14-662-labor-economics-ii-spring-2015/recitations/MIT14_662S15_Recitation10.pdf
The OLS regression is equivalent to a MLE fit of the form
y = mx + b + normal(0, sigma)
The asymmetry over reflection comes down to which variable has the normal(0, sigma) term.
Since the problem is framed as “who’s over/underpaid”, we’re considering pay to vary and the other to be fixed. i.e. we need to presuppose that players could have hypothetically been paid something else for statements about over/underpay to make sense. We’re choosing what to pay for a fixed performance. So y should be pay.
The reflection is for evaluating post-hoc performance. We’ve already paid everybody, then the next season comes out and we measure their performance, then we can say who under/overperformed.
This isn’t supposed to be a trick question, but considering it as a trick question, I wouldn’t expect franchises to pay for per-player performance. Highly concentrated performance is more valuable to the franchise from a revenue perspective–superstars drive merchandising, name recognition, sales. I expect a mostly average team with a superstar makes more money than an above average team that wins the same amount with all consistent performers. As such, I’d consider Tom Brady to be more valuable than just his wins above replacement.
Another trick answer: assuming increasing an employee’s salary doesn’t cause them to perform better at the same position, there’s no such thing as an underpaid employee from a firm’s perspective. Given that the these are realized salaries that the players ended up receiving, whoever paid the amount written DID get the player and was not outbidded, so they evidently didn’t pay too little. From this perspective, every player was overpaid by their respective franchise with some small epsilon.
There’s a confounder in the data as well: in recent years, the NFL’s salary cap goes up every year (with the exception of this year due to the pandemic), sometimes by as much as $10 million per team. Thus, one would expect “overpayment” for any new contract.
Supposed overpayment in 2013 quickly becomes underpayment just a few years later, as a look at Patrick Mahomes’s deal will show you!
Isn’t this the adjustment being made in “adjusted cap hit”?
Ah, yeah that’s certainly possible!
Both graphs are of players’ contracts, and their performance while they’re under that contract.
Players are given contracts based on their expected performance. Then their actual performance while they’re under that contract is higher or lower than expected, but on average it matches their expected performance, which is what their contract was based on.
So we can say that, at every price point, on average teams get what they pay for. At a given contract size, the players who outperform that contract balance out the ones that underperform.
But we can’t say that, at every level of performance, on average players are paid what they’re worth. Because high levels of performance will include more players who overperformed their contract (and thus are underpaid for their performance), and low levels of performance will include more players who underperformed their contract (and thus are overpaid for their performance).
Brian 1’s graph matches the “do teams at every price point get what they paid for?” question. e.g., It shows that teams that pay a quarterback $15M on average get 6 EPA of performance from that quarterback while he’s under that contract. That’s what the regression line is plotting. So that regression line represents fair value – if a player is on the regression line then the team is getting what they paid for. At the time the contract was signed, the team expected the player to be at the $15M, 6 EPA point (on average).
Brian 2’s graph matches the “do players at every performance level get paid what they’re worth?” question. e.g., It shows that quarterbacks who produce 10 EPA are doing so under a $10M contract, on average. That’s what the regression line is plotting. And that regression line does not represent fair value – quarterbacks who produce 10 EPA are on average overperformers, so getting paid the average level of the 10 EPA quarterbacks means that you’re underpaid, not fairly paid. At the time the contract was signed, the team did not expect the player to be at the 10 EPA, $10M point (they expected lower EPA).
So Brian 1 is right that Peyton Manning is underpaid, and that if Aaron Rodgers’s future performance matches his past performance then he will be underpaid.
Brian 1 is too glib about assuming that Rodgers’s future performance is likely to match his past performance. But rather than calling him out on that and investigating the question of Rodgers’s expected future performance, Brian 2 instead did a different thing.
Phil, in the original comments, seems to be reading graph 2 to say that if a player produced 10 EPA under one contract, then under the next contract we should expect him to be worth $10M. But that is not what graph 2 is plotting – it shows that players who produced 10 EPA were (on average) playing under a $10M contract that they had previously signed. And since their performance since they signed that contract has been much better than was expected, presumably their expected future performance is now higher than it was back when they signed the $10M contract ($10M is the prior, 10 EPA is new data, we need to update).
(I also left a comment on the MR post, but I think this is better distilled.)
Nicely done. The only adjustment I would make is that your notion that EPA accurately reflects the expectation of the teams and the outcome of the bargaining process. That’s an assumption of your model, not an aspect of the world. Thus, if EPA were grossly inadequate in some way to reflect performance worth paying for, the notion that the regression line reflects fair pay would be wrong.
Good point. My case against graph 2 is stronger than my case for graph 1.
To try to be more systematic about it, we can divide the mismatch between salary & performance into 2 sources:
A. Things that were known at the time the contract was signed. That is, mismatch between salary & expected performance.
B. Things that weren’t known at the time the contract was signed. That is, mismatch between expected performance & actual performance.
If the mismatch is entirely due to B and not at all A, then graph 1 is a reasonable way to look at things. I took that as a modeling assumption in making the case for graph 1. (Some other commenters have brought up the case where graph 1 has a horizontal regression line and noted the absurdity it implied, but according to this modeling assumption we will never find a graph 1 with a horizontal regression line, except from noise.)
If the mismatch is entirely due to A and not at all B, then graph 2 is a reasonable way to look at things. In that case, the average cap hit of the players with 10 EPA (for example) would be the average salary given to players who were known in advance to be 10 EPA quarterbacks, and so it would make sense to group them together the way graph 2 does (and my argument against graph 2 would not go through, as it assumed that B mattered).
In both cases, further arguments are needed for treating the regression line as the fair salary, and the residual as representing how overpaid or underpaid the player was. For example, in graph 1 if positive residual represents players who got lucky on the field & outproduced their skill level then it maybe doesn’t make sense to consider them underpaid – though there are different notions of “underpaid” so maybe you could. And with graph 2, maybe the mismatch between salary & expected performance happens because some players knowingly take a discount because they want to play for a particular team, and some teams knowingly “overpay” a player because the GM is worried about losing his job if he lets the fan favorite quarterback leave; the regression line defines “fair pay” as when each of these factors is at its average level but an alternative notion of “fair pay” would define it as the salary that a player would get based purely on performance if these factors were set to zero.
If there’s both A & B involved then neither graph really works. My guess is that B is a bigger factor than A, so I think graph 1 is closer. Also, I think (for reasons outside the bounds of these analyses) that good quarterbacks tend to be underpaid on average, so the errors from using graph 1 partially cancel out those other errors.
The data is not the same between the two graphs. “12-A.Rodgers” is clearly labeled on both graphs at different points. About (12, 11) on the top graph and (10, 9) on the bottom graph.
Agreed I think something is wonky
Right? The graphs don’t make sense.
‘Tis just a labeling problem. The same three points are in the “medium salary, high performance” cluster in both graphs. One is unlabeled in both. One is labeled 9-D.Brees in the first and 12-A.Rodgers in the second. One is labeled 12-A.Rodgers in the first and 12-T.Brady in the second. Presumably the three points are Brees, Rodgers, and Brady in some order.
I suppose this argues against Andrew’s preference for labels over dots. With dots, less can go wrong.
Actually, none of those three points is unlabeled in both. The one with the lowest salary and middle performance is labeled “12. A-Rodgers” in the first and second charts. The one with the middle salary and low performance is labeled “9.D-Brees” in the first chart and unlabeled in the second chart. And the one with the high salary and high performance is unlabeled in the first chart but labeled “12. T-Brady” in the second chart.
It seems safe to conclude that the low-salary/middle-performance point represents A. Rodgers, the middle-salary/low-performance point represents D. Brees, and the high-salary/high-performance point represents T. Brady.
You’re right. In the first chart it’s actually ambiguous which point “12. A-Rodgers” refers to, but your solution is simplest.
I’m not even sure if we should be thinking about the regression line or its 95% CI’s when evaluating bang-for-the-buck. For the first graph, I’m more interested in calculating an efficiency frontier–lines that connect the players closest to the top-left corner of the graph. The line is concave and would connect Cassel, Hill, an unlabeled point (Brady), and 12.AaronRodgers as best value, and the inverse of the slopes of the line segments represent tradeoffs in incremental dollars per performance. The closer the slope is to 0, the greater the incremental cost per incremental performance. Players connected by these line segments indicate best value per dollar spent–all players below and to the right of the connected points are dominated, from an economic sense. This would indicate that the new Aaron Rodgers point is not quite good value–it’s slightly dominated by 12.AaronRodgers (old contract?).
The second graph tells the same story, but the frontier would be convex in nature, connecting points closest to the bottom right of the graph (same players would be on the frontier). The steeper the slope (closer to infinity), the worse value (greater incremental cost per incremental performance). The same players would be considered “good value” as the other analysis.
I dispute the premise of the challenge.
Looking at either graph makes it obvious that this data can’t be used to value this contract and nothing good would come from taking it seriously. Neither ‘Brian’ is right.
There’s a weak linear connection between X and Y (it doesn’t matter which is which). Clearly neither ‘explains’ the other that well. To make the problem more blatant, though, imagine the correlation to be even weaker (or even zero).
If we look at a sample point y chosen specifically such that y is much greater than mean(Y), it’s almost surely going to remain anomalously large “given x” and any weak Y~X model. The question Brian is asking is “how extreme would we need to change the inputs of the model to explain ‘y’, but the model *doesn’t* explain Y – only part of it – so why is this interesting? The answer is going to be that: maybe the model can’t be manipulated at all to predict this “y” (e.g. if there really isn’t any correlation) or even if this is possible, the weaker the model the more extreme and implausible we will need to contrive hypothetical inputs to get extreme outputs.
With many points to choose from, we can presumably find ones which are extreme in *both* X and Y and thus we will get silly answers trying to force both a weak Y~X or X~Y model do what they never claimed to do. In this example, the model is only _fairly_ weak and the Brians’s inferences are not prima facie silly, but that just obscures how meaningless they are.
Rodgers is a data point presumably chosen because it’s extreme/abnormal, and so either linear model (manifestly not that complete as a predictive model anyway even for ‘randomly chosen’ points) can be expected to be even more insufficient. The graphs are telling us: to understand this specific contract at all you must look for a better model. You’d like a better model in general, of course, but you _really_ need one here; don’t just pretend what you’ve got can be used as either Brian does.
Pick any number between 0 and $20M. I pick $10M.
Graph 1 shows that if you meet a quarterback and find out she is paid $10M, then you expect she has added 4 PPG to her teams.
Graph 2 shows that if you meet a quarterback, find out her stats and find they are +4 PPG, then you expect her to be paid $6M.
It bothers the Brians that these are not symmetric. Maybe there’s a million possible reasons, and we can’t choose between them. They just aren’t.
So, knowing that Mr. Rodgers adds 10 PPG based on past performance, we would suppose he is paid about $10M. In fact, he has been paid slightly less than that. And he is about to be paid twice that, if I remember right. And on discovering his new large salary, we can expect he will perform… a bit worse than he has been. So the bum deserves to be overpaid.
(Other consideration are football related, and therefore out of scope.)
I asked the Brians about another problem. In R let:
x = c( 0, 0, 1, 1, 2, 2 ); e = c ( -.1, .1, -.1, .1, -.1, .1 ); y = x + e; w = x + 10 * e;
The Brians just quibble when regressing x with y, but are back to fighting bitterly when it’s x and w.
Brian1 says it is more than a little obvious that the regression line is slope 1 and intercept 0 in both cases.
Brian2 says that nevertheless
foo <- lm( x~w ); plot( w, x ); abline( foo );
looks like the right fit and he gets x = .4 * w + .6
Brian 2 is correct. Consider for instance the example where actually there is almost no correlation between pay and performance. Then you would end up with a very flat trendline, and you’d get from Brian 1 the conclusion that Rodgers is worth an almost infinite amount of money. In comparison, under Brian 2’s method, as correlation decreases towards zero you will get the sensible conclusion that the degree to which Rodgers is overpaid should be just his difference relative to the average.
I’m sure there’s a more mathematical way to show this but hopefully this is fairly intuitive.
I mean really it should be sufficient to just note that Brian1’s methodology implies a bunch of below average performing stars should be fined millions of dollars to suspect that Something Has Gone Wrong.
Hey—you don’t fine someone just cos they were overpaid!
Unfortunately knowing Brian 1 is wrong does not imply Brian 2 is right.
Brian 2 is less wrong, and less expensively wrong! That’s good enough, as per George Box…
Good point.
Good point. I’m convinced by this. Both Brians are looking at differences in money paid conditioned on EPA/G, and Brian 2 sets up the regression for that.
Brian 1 also says:
> The vertical distance between his new contract numbers, $21M/yr and about 11 EPA/G illustrates the surplus performance
That makes sense though, right? And it would be similarly weird for Brian 2 to say, “If you extend the line to the right in my plot, you’ll find Rodgers is underperforming by 10 [or whatever] EPA/G and so is clearly overpaid” (you get the same basically-infinity-if-near-zero-correlation sort of problem).
Yes, I believe so.
This came up recently with twitter excitement about a study about dating preferences. There was a big table showing “how much additional income you would require to be as attractive if you change a prospective partner’s height by one inch” that got people very excited by the big numbers.
But if you looked at the study itself, really the lesson is how poor income differences are as an explanatory variable…
Aaron Rodgers is overpaid. So are all the other quarterbacks.
There, that was easy.
Oh, wait, you want to also assume that quarterbacks are paid fairly on average? OK, then…
Brian 1 shows that the team is paying Rodgers less than they need to get the expected performance. Hence, underpaid. The team gets a good deal.
Brian 2 shows that Rodgers is getting more than expected given the performance. Hence, overpaid. Rodgers gets a good deal too.
Everybody wins!
This is easier to think about if you imagine (or draw) both regression lines on the same plot. You’d see that the two lines are not the same, and that Rodgers happens to fall in-between them. Thus, he looks overpaid compared to one regression and underpaid compared to the other.
This outcome becomes less surprising if you consider the extreme case where EPA/G and and salary are completely uncorrelated. Then one of the regression lines would be almost horizontal (slope almost zero), while the other would be almost vertical (slope also almost zero, but with respect to the other axis). Thus, there’s a lot of space in-between the two regressions and it’s easy to find “anomalous” points like Rodgers. Of course, if the two quantities were fully uncorrelated, then the error bars on those regressions would be very broad, as well. The thing that makes the example here work is that there is a correlation, but a weak one.
The other question of course is which Brian is right? Is Rodgers overpaid or not? I think the most relevant plot for that is Brian 2’s: after all, I’d expect the players’ EPA/G to stay about the same regardless how much they’re paid. But also, the actual salary is based on some balance between supply and demand, so it seems to me like the question is a bit ill-defined. I can see the employer using Brian 2’s argument (for this amount of money we could hire all these other players with similar EPA/Gs) and Rodgers using Brian 1’s (I’m scoring this much better than other players so I’m expecting to get paid that much more) — and then negotiating from there.
The linear functional relationship assumption is problematic due to resource scarcity. One cannot buy two $5m players to get $10m value.
But, setting that aside, as others have already mentioned, EPA/G is measured with error. One could debate whether salary has error. It is observed exactly, but may be an imperfect measure of ‘value’.
I propose a Brian 3 approach: Deming regression, assuming error in the measurement of both.
If I were to bring in other information…I’d say that one cannot get a good estimate from these data alone. Salary is a complex function of value to the team and scarcity versus other market options. And value reflects an overall revenue management including merchandising, butts in seats, and more.
Maybe I’m missing something but the dilemma if there is one seems simple unless I am missing a trick inside another. Consider an X-Y plot of 2 straight lines S1 perfectly correlated points (at 45* for simplicity) and S2 at a slightly smaller slope and a small intercept on Y axis. S2 represents the less than perfect correlation. Swapping X & Y axes will produce different correlations for S2 but not S1. The further out on the S2 line the greater the discrepancy, so an opportunity to cherry pick your bounds.
Amy Noether can rotate and translate axes but can celestial bodies be moved to suit the axes? Maps and territories.
Correlation between X and Y = correlation between Y and X
It’s symmetric.
corrrelation is comparison which can be express that the point X,Y is at the point Y,X Its conditional on the location of the points. Without points of each factor, the questions is false or not possible to answer.
Just pointing out that we’re now on day 13 since you promised to post your answer in “a day or two.” I don’t know about others, but I am interested in seeing it!
+1
+1
Hope there’s not a 6-month embargo on the solution.
Ongoing extended contract negotiations. We could trade him for another Qualified Bayesian.
So when is the solution coming? Been checking weekly since August!
+ 1