Ryan Bernstein shows this demo of a prototype of the network of models visualization in Stan. This is related to the topology of models, an idea that we’ve discussed on occasion and is a key part of statistical workflow that I don’t think is handled well by existing theory or software. What Ryan is doing seems like a good start!
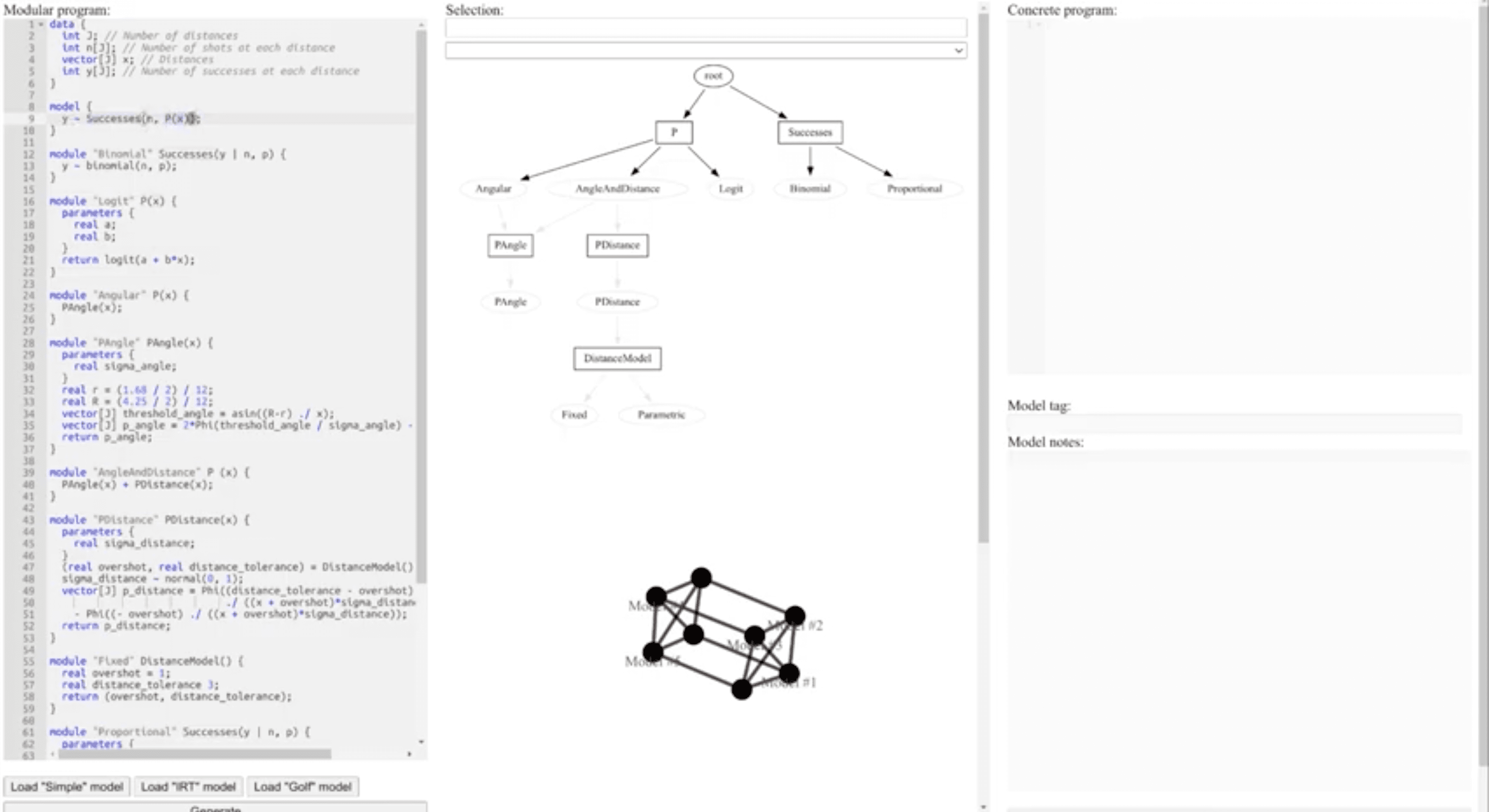
So the goal here is to procedurally define a universe of models and automatically visualize their graphical representation? Can it handle, say, repeated structures via e.g. plate notation? I do like the model network visualization down below in the middle panel; the whole framework reminds me of “symbolic regression”, which is something that’s always interested me and when used to generate an ensemble of models appealed to me over e.g. stepwise regression. Has there been any progress on those grounds, either in tractably fitting a large universe of possible models or else regularizing over models to prevent overfitting (my impression was that you’re very susceptible to overfitting if you exhaustively fit whatever combinatorial explosion gives rise to a large universe of possible models, esp. in way that traditional model comparison / averaging tools cannot handle). If one solution to multiple comparisons is defining some hierarchical structure to model parameters, can we regularize by defining some hierarchical structure over possible models, e.g. specify a dirichlet(a,a,a,…) prior over models with, say, some exponentially distributed concentration parameter *a*, and then use model marginal likelihoods to obtain a posterior distribution of model probabilities?
(a dirichlet so parameterized would necessarily be varying degrees flat or uniform over all the candidate models, though… I do wonder if it would be possible to specify a distribution over the network with parameters capturing both central tendency and dispersion? Maybe something where you have a discrete “mean” model node and mass proportional to, say, the minimum number of edges some other node is away from it? The only other context I’m really familiar with in which probability distributions are defined over graphs is phylogenetics, using e.g. variations on the birth-death process, but that’s specifying distributions over graphs and not nodes in a fixed graph)