(This post is by Yuling, not Andrew.)
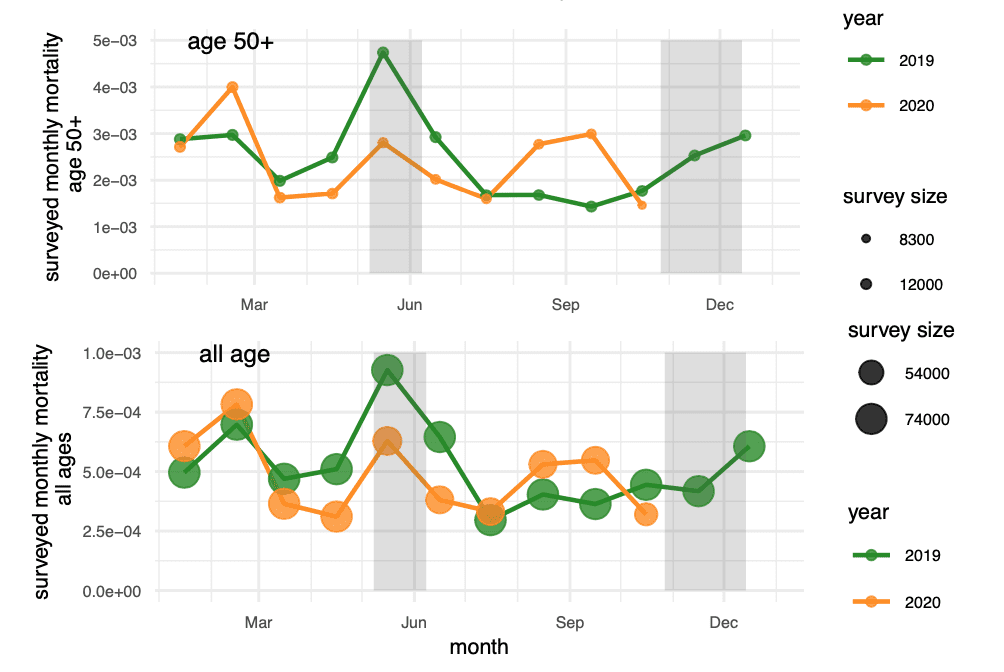
We like bubble charts. In particular, it is the go-to visualization template for binary outcomes (voting, election turnout, mortality…): stratify observations into groups, draw a scatter plot of proportions versus group feature, and use the bubble size to communicate the “group size”. To be concrete, below is a graph I draw in a recent paper, where we have survey data of mortality in some rural villages. The x-axis is the month and the y-axis the survey mortality rate that month. The size of the bubble is the accessible population size under risk during that month. I also put the older population in a separate row as their mortality rates are orders of magnitude higher.
When we make a graph comparison we always have a statistical model in mind: the scale (probability, log probability, log odds…) implies the default modeling scale; one standard error bar corresponds to a normal assumption, etc. Here, as you can imagine, we have a hierarchical model in mind and would like to partial-pool across bubbles. Visualizing the size of the bubbles implicitly conveys the message that “I have many groups! they have imbalanced group sizes! so I need a Bayesian model to enhance my small area estimation!”
OK, nothing new so far. What I want to blog about is which “group size” we should visualize. To be specific in this mortality survey, should the size be the size of the population (n), or the number of death cases (y)? I only need one of them because the y-axis indicates their ratio y/n. This distinction is especially clear for across-age comparisons.
It is common to pick to population size, which is what I did in the graph above. I also googled “gelman bubble chart election”, the first result jumping out is the “Deep Interactions with MRP” paper in which the example visualized the subgroup population size (n) of income × ethnicity × state group, not their one-party vote count.
But I can provide a counterargument for visualizing the case size (y). Again, a graph is an implicit model: visualizing the proportion corresponds to a Bernoulli trial. The inverse Fisher information of theta in a Bernoulli (theta) likelihood is theta(1-theta). But that could be wrong unit to look at because theta is close to zero anyway. If we look at the log odds, the Fisher information of logit(theta) is theta(1-theta). In the mortality context, theta is small. Hence the “information of logit mortality” from a size-n group will be n* theta(1-theta)≈ y, which also implies an 1/y variance scaling. This y-dependent factor will determine how much a bubble is pooled toward the shared prior mean in a multilevel posterior.
In this sense, the routine of visualizing the group size comes from a rule-of-thumb 1/n variance scaling, which is a reasonable approximation when the group-specific precision is roughly a constant. For a Bernoulli model, the reasoning above suggests a better bubble scale could be n*theta(1-theta) ≈ y(1-n/y), but it also sounds pedantry to compute such quantities for raw data summary.
Yuling:
This is not directly relevant, but there’s also an issue of how large should the circles be: should their diameters scale with X or sqrt(X)? Cleveland’s classic graphics book from 1985 cites research that says that neither scaling really matches with perception, and he discourages using area to convey magnitudes, as areas are hard to visually compare. But sometimes circles are appealing.
When I made the bullseye plots for the penumbra paper (see figure 2 here), I scaled the diameter with sqrt(X), which has the benefit of compressing the dynamic range and making small changes easier to see.
Andrew,
I would add that it is also relevant to your discussions on which Bernoulli trial is more “informative”/”stronger”: theta close to 0 or theta close to .5? The answer depends on whether to look at theta or logit theta, which further has implications on experiment design and prior specification.
“he discourages using area to convey magnitudes, as areas are hard to visually compare”
Yes, I think that impacts these charts. The charts *are* visually appealing and most of the info comes through great but the survey size represented by the circle size is somewhat unclear. Definitely it’s ez and quick to see that the two charts have different circles sizes. I think that’s what Yuling is trying to convey and that comes through fine. But within the charts it’s not possible to distinguish the sizes at web page scale, yet there is a scale for each chart suggesting that there’s some reason to understand the relative sizes within each chart.
Also one thing I detest about most modern data software is that the subdivisions of size are commonly equally scaled or divided over the data range and thus have weird number boundaries, as is the case here, rather than using standardized increments that people actually understand.
For my money while I like this chart it could be improved by having only one legend for each symbol type – with the circle sizes illustrated on a single legend with rational sizes, like “25K, 50K, 75K”.
Jim, I actually pick the legend as the approximately max and min sample size in the chart.
Oh, I missed that. That makes more sense to me then. Wonder if you could add that to the legend titles.
Visualizing n is more concrete, potentially less prone to readers mistaking what they see, but for a stats paper visualizing y seems fine. But is that one size encoding used across both rows? If so, I would get rid of the extra “survey size” legend label for the second size legend, since it makes it seem like you have two separate encodings. You could do log n or y to get the circle sizes to vary (or sqrt like Andrew suggests) more but if you do I would make that clear in the legend label (ie Log survey size).
Yes all of this options are valid for visualization. I just think that sometimes we interpret bubble size as “weight of the group”. In the analogy of sample survey, there is only one correct way to compute group weights and I should not take a log or sqrt transformation just in order to make my table look nicer.
Bubble size also conveys how balanced the design is. In this particular example, the total sample size (n) between older people and younger people is quite imbalanced, but the death case (y) is more balanced.
If you want to get fancy there are other aspects to consider. The Bubble Chart Master is undoubtedly the late Hans Rosling. He used them dynamically to visualize the effect of time. What is the right speed for this? Should it be uniform or perhaps we could have a variable speed reflecting uncertainty in the data https://www.gapminder.org/fw/world-health-chart/
Hans’ charts are great but in part that’s a function of the scale of the effect. Bubbles work well for large changes / differences.
yet another dimension we played with some time ago, is to use sound on a dynamic bubble chart. Of course the size of the effect matters – let the data “speak”….
Rectangles? I have never seen any research on size estimation with rectangles but perhaps the perceptual psychologists have done some?
It is not clear to me if the problem is “size” or humans’ difficulty in estimating volume in a circle.
I really like this post. Did something similar a while back for visualizing empirical cumulative logits.
A related option might be to include “internal evidence error bars”, i.e. derived from the MLE fit separately at each point.
However, I think an error bar conveys different information from the corresponding precision/information weight; the weights are on a different scale (“n”) and arguably need only be proportional.