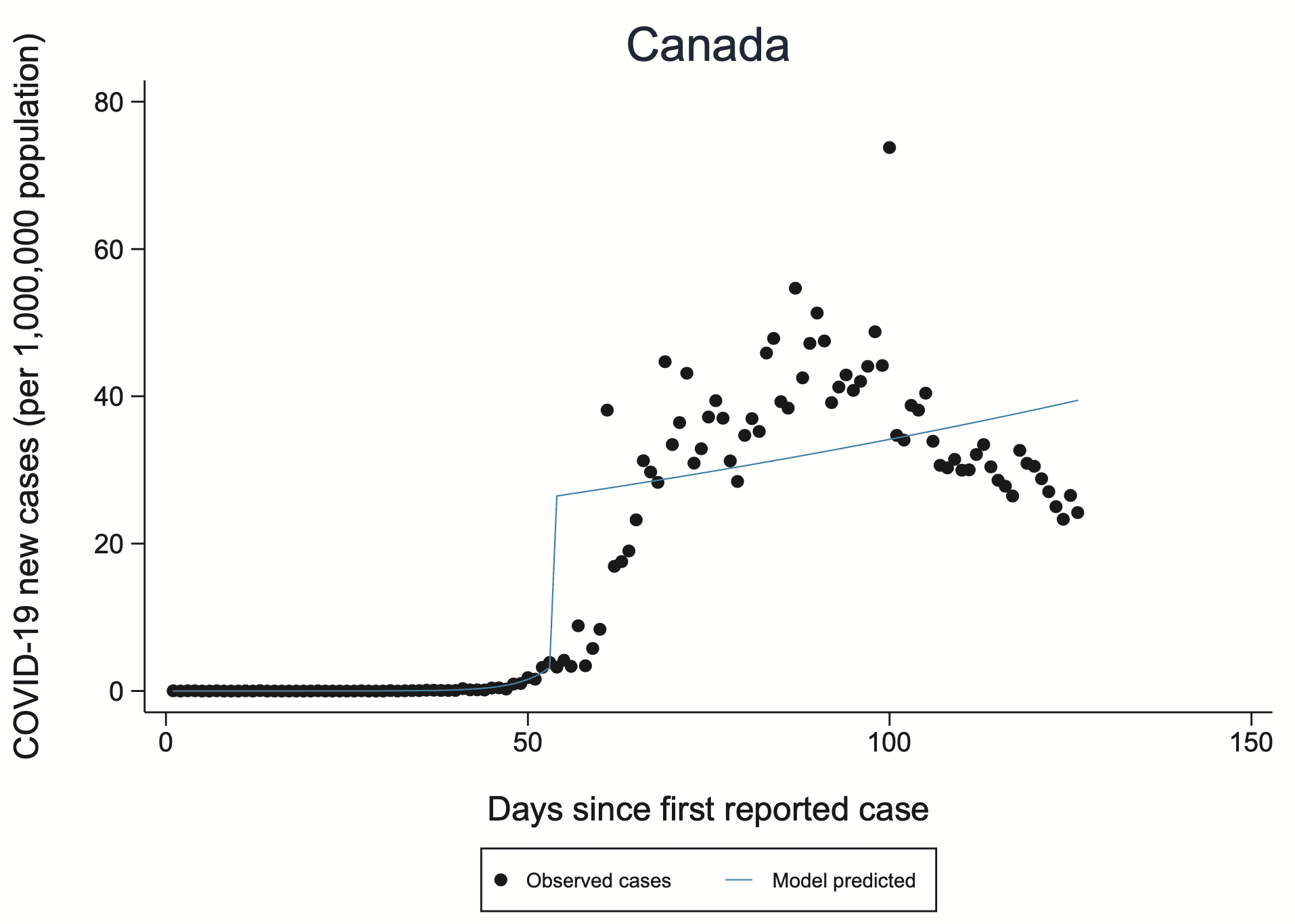
A biostatistician writes:
The BMJ just published a paper using regression discontinuity to estimate the effect of social distancing. But they have terrible models. As I am from Canada, I had particular interest in the model for Canada, which is on their supplemental material, page 84 [reproduced above].
I could not believe this was published. Here they are interested in change in slope, but for some reason they have a change in intercept (a jump) parameter, which I find difficult to justify. They have plenty of bad models in my estimation.
For completeness, here is the main paper, but you don’t even need to look at it . . .
Please, I would like not to have my name mentioned.
I agree with my correspondent that this graph does not look like a very good advertisement for their method!
Why did the British Medical Journal publish this paper? It’s an important topic, maybe none of the reviewers actually read the paper carefully, maybe it’s actually a wonderful piece of science and my correspondent and I just don’t realize this . . . the usual explanations!
I’m guessing that medical and public health journals feel a lot of pressure to publish papers on coronavirus, and there’s also the same sort of fomo that led to the Journal of Personality and Social Psychology publishing that ESP article in 2011. Never underestimate the power of fomo.
P.S. The article has some peer reviews. See P.S. here.
Authors seniority positions are: senior statistician; professor of mathematical epidemiology; professor of social epidemiology; senior clinical research fellow; professor of biostatistics, mathematics, and statistics; professor of mathematics and statistics; professor of population health research.
These people shouldn’t be trusted to do data-entry, let alone hold their “esteemed” positions. What a joke.
The supplemental graphs are morbidly fascinating. I especially recommend Turkey and Singapore. The pandemic is making even clearer something that was clear enough before: far too many scientists have a very poor grasp of quantitative data and models, though that doesn’t stop them from analyzing and modeling.
“The pandemic is making even clearer something that was clear enough before: far too many scientists have a very poor grasp of quantitative data and models, though that doesn’t stop them from analyzing and modeling.”
+1
> many scientists have a very poor grasp of quantitative
Have you looked at the author’s affiliations?
Yes.
And?
The last author, by the way, has 12 papers in 2020 so far (not counting this one); I hope he gave the 300 pages of supplemental material the attention they deserve.
Raghu:
I have 14 papers in 2020 so far (if you count those that are scheduled to be published) . . . it’s ok to be busy!
I’m impressed! I only have two. I’ll get back to work now…
The Singapore chart is especially worrying as it states that public transport was closed about a week after schools were. I can attest that the metro and buses have been running nonstop throughout the pandemic in Singapore. The lockdown date for Singapore is also wrong. Makes me wonder, how accurate the data are for other countries.
Andrew – it’s not fomo. These journals are getting more articles on covid than they could ever possibly publish. It’s just more of the same as always.
Joshua:
OK, let’s go with “none of the reviewers actually read the paper carefully” as our tentative explanation, then.
Sorry, there is no peer review to display for this article https://www.bmj.com/content/370/bmj.m2743/peer-review
Keith:
Now there is; see P.S. here.
Couldn’t you argue that there’s a structural break in the graph, thereby justifying the need for two regression models, one before the pandemic took off in the country and one after? Not a statistical expert by any means, but that’s what I had thought. Would love to hear the reasons why that’s not appropriate in this case!
Interested:
There are all sorts of models that could make sense, in theory. But in this case, the here’s no reason to expect a jump (you can see this based on the discussion in the linked article, where among other things they talk about an approximate 7-day lag, which would already blur things a bit). Also the model doesn’t fit the data, as can be seen from the graph. And that’s all before getting into data quality issues, such as the number of new cases depending on how many people are tested.
This is a good question. In addition to Andrew’s answer:
1 The thing being plotted (new cases) cannot be discontinuous. Even if one imagines the sudden appearance of viral particles, unleashed as one open the magic box that contained them, the realities of incubation, detection, infection, and transmission would make the new cases a smooth function over time. Therefore, fundamentally, it makes no sense to fit this to a discontinuous function, as the authors have done. (One might more realistically imagine that the rate of change is discontinuous — still likely wrong, but less egregious.)
2 Sometimes one models continuous things as being discontinuous and it’s fine; this isn’t the case here. For example: if I model the current through a circuit at times before and after I close the switch, the current is zero beforehand and some finite value later. I could pretend the data are fit by a step-function (zero, then suddenly some constant value), and this would be fine if what I care about is the “steady state” much after or much before the brief interval around the switch being thrown. In this case, though, I can’t claim that my model describes the behavior around the switch throw. If I care about that period, I have to understand the features that make the current continuously rise from zero to some value (not hard to do), and incorporate them into my picture. Here, all the action we care about is, in fact, in this rapidly changing period, not some “steady state.”
3 Any data can be fit by any model. Always. Therefore, at the very least, one has to look at *how well* a particular model fits the data. Here, it’s pretty awful. In general, such poor agreement is a strong indication that one’s model does not convey any insight into the actual mechanisms that generated the data.
It looks like the jump occurs due to coefficient beta2 in their main regressions. In the text, they describe it as, “beta2 represents the change in the level of outcome immediately post-intervention.” In other words, the jump separates pre- and post-intervention periods, not pre- and post-pandemic taking off.
I tried to figure out why they would include the jump. Sensibly, the main goal of the authors is to understand how interventions affect the exponential growth rate of COVID-19 cases over time. They are interested in the change in exponential growth from pre- to post-intervention, and not the jump itself. But why include the jump at all? The literal interpretation of the jump is ridiculous… for Canada, it is that the lockdown and other restrictions caused an immediate, large increase in the incidence of COVID-19!
If one were to nicely fit a nonparametric, smooth curve to the COVID-19 incidence data, and compare average exponential growth rates pre- and post- intervention, it is possible one would get similar effect estimates to those obtained by the authors with their simpler regression model that has a constant (exponential) trends and a jump. It feels like there would even be statistical guarentees of this, and it could explain both the jump and the authors’ apparent lack of embarrassment about the terrible model fits (such as seen for Canada). But the authors don’t take the time to state any of this, so far as I could see.
Considering that, the problem with this study may not be the terrible model fits, but the authors incomplete explanation of their statistical approach.
Additionally, I am unconvinced by the authors’ attempts to address differences in test availability between and within nations. It looks like their analyses do not even include data on changes in test availability within nations.
Well, it turns out that none of the editors’ or reviewers’ comments on this article addressed the terrible model fits or the jump parameter in the regressions.
There are 13 pages of editor and reviewer comments, yet the model fits are only mentioned in a statement that some of the curves fit the data “almost too well” and a statement complimenting the authors for their presentation of the incidence data and fitted models. Remarkable.
More:
Yup. Peer review is done by peers.
Andrew, Some great points in the post you link. Thanks!
Contrary to what the correspondent writes, this is an interrupted time series model, not regression discontinuity, and they do include a parameter for change in slope.
What box you place the analysis into is a red herring IMHO. Whatever you call the technique the authors used, prima facie it appears to be a rather substandard way of analyzing the data. The most obvious way to see this is that the number of detected positive cases is highly correlated with the number of tests (as well as base rate in the population, selection of people who get tests which changes over time, etc.). According to the statistical analysis of the paper they didn’t take any of that into account. Moreover, even if they did, the fit is still terrible; both from a residual errors standpoint, and from the fact that background knowledge would apriori place the plausibility of such a dramatic step function to be quite low.
Reading a bit more thoroughly (read: somewhat less cursory) they at least acknowledge that testing rates may have an impact. But did not include it in the analysis due to lack of quality data. That makes me feel a little better, but still, it’s just a terrible way to do this. The obvious way is to include testing rates in the model and see under what conditions the testing rates matter, and report a panel of scenarios; as opposed to leaving it out entirely.
“We attempted to collect data on covid-19 testing rates by country, but we could only identify data for 112 countries from a variety of sources, and the validity of these data might be questionable. The outcome metric in our study was incidence, which could be influenced by testing rates. However, testing rates were potentially stable during our study period, as we restricted the analysis up to 30 days post-intervention implementation; covid-19 testing rate was not found to be a significant factor in our meta-regression analysis.”
If you skim read the main paper and don’t look at the supplementary data then it looks like plausible work – there’s talk of a meta analysis and and equation/model with fancy looking terms. I suspect the reviewers were at least as far outside their areas of expertise as the authors.
On a related note I really don’t like reviewing papers with important information in the supplemental part. If including it makes the paper too long for the journal then find another journal.
Given that the Supplementary Material section is over 300 pages long, I wouldn’t be terribly surprised if it wasn’t carefully scrutinized. Some of the individual-country fits (which is most of the 300 pages, I think) look sort of OK, some look like the Canadian example.
Peter:
Yah, and the funny thing is, had they just submitted the paper as is with no supplementary graphs, it probably still would’ve been published and featured in this top journal, but then we wouldn’t be criticizing it because it wouldn’t be so obvious how bad the model is.
It reminds me of that air-pollution-in-China example.
In both cases, I appreciate the honesty of the authors in including the graphs, even while being bothered that they seem to not care how weird the model looks. In both cases, I think there’s a blind faith in statistical techniques, so much so that they wacky model fit doesn’t set off any alarms for them.
Yes, looking through the graphs I have to wonder if they even thought that evidence mattered. They had a model and fit it to every country – and, look – there are graphs showing results. Would there have been any fit that would have caused them to question their model? It doesn’t look like that to me. It adds up to very strange research practices.
Daniel:
Yes, same as with the air-pollution-in-China example. They have a trust in their method. Someone told them the method was unbiased or has good theoretical properties or whatever, and that’s it.
Note also in the peer review response (https://www.bmj.com/sites/default/files/attachments/bmj-article/pre-pub-history/author_response_7.7.20.pdf) they did agree to make the data available, and they have done so here: https://github.com/shabnam-shbd/COVID-19_Physical_Distancing_Policy. I give them credit for posting the data, which is a good thing, but there is no code (as far as I could see), so really no way to understand exactly how they produced this ‘evidence’. I suppose one could take the time to try and reproduce what they have done but it feels like diminishing returns at this point…
Might one of you post a rapid response to the BMJ paper itself, summarizing your questions, concerns and criticisms? That way the authors can respond and readers will be alerted to the discussion. Peer reviews are generally posted a week or so after the paper first goes online. It’s not an automated process. The editorial assistant who collates and posts these does her best to get them up with the paper but it’s not always possible. I believe they are up now.
Elizabeth:
Thanks for the information. I will suggest to the person who wrote me the original email that he post a rapid response.
It looks like they tried an interrupted time series, not a regression discontinuity design.