That’s the title of a recent article by Yuling Yao, Aki Vehtari, Daniel Simpson, and myself, which presents some diagnostics for variational approximations to posterior inference:
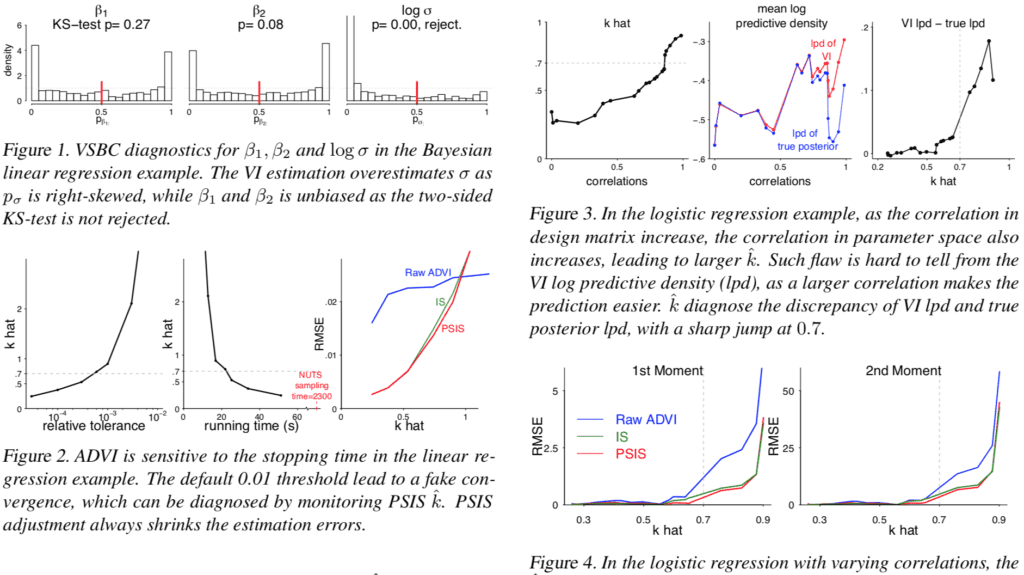
We were motivated to write this paper by the success/failure of ADVI, the automatic variational inference algorithm devised by Alp Kucukelbir et al. The success was that ADVI solved some pretty big problems very fast; the failure was that in lots of examples, ADVI gave really bad answers. We’re still working on figuring all this out—a big issue seems to be scaling, as some of the most horrible disasters are occurring when parameters are far from unit scale. One issue here is that it’s easier to come up with a method than to get it to work reliably, another seems to be a problem in academic incentives, where there’s more of a motivation to attack new problems than to get old things working.
In any case, on the way to trying to fix ADVI and develop a practical automatic method, we thought it could make sense to formalize some of our approaches for checking how well it’s working, as there are various ways that a variational solution, or estimate, can be compared to the full objective function (in Bayesian terms, the log-posterior density).
For an outside perspective on this work, here’s a post by Stephanie Hyland suggesting some directions for future research.
It’s probably worth saying that if anyone is at ICML, Yuling will be giving a “long” talk on the paper. (I don’t remember what “long” means in this context)
I’m late to this thread, but I love the PSIS diagnostic for VI in this paper. We’ve only started experimenting with it in our work recently but it seems much more stable and informative than the ESS.
On the other diagnostic (uniformity of posterior p-values) I should promote a small twist on this idea we published a few years ago (https://arxiv.org/abs/1301.3166): just testing it for data similar to the observations. The idea is that this is a less stringent requirement than good inference for all possible data sets.