This post is by Aki
Last week Xi’an blogged about an arXiv paper by Chatterjee and Diaconis which considers the proper sample size in an importance sampling setting with infinite variance. I commented Xi’an’s posting and the end result was my guest blog posting in Xi’an’s og.
I made an additional figure below to summarise how Pareto shape parameter and Pareto smoothed importance sampling is related to this. You can read more in our arXived paper with Andrew.
When MCMC got popular, the reasons why IS got less popular were 1) the problem of finding good proposal distributions and 2) possibility of getting infinite variance for the weight distribution (which leads to infinite variance of the IS estimate). If the variance is finite, the central limit theorem holds and people have (mostly) assumed that everything is going to be fine, and if the variance is infinite people have assumed that all hope is lost.
Chen and Shao (2004) showed that the rate of convergence to normality is faster when more higher moments exist, so it’s useful to examine the existence of higher moments, too. Koopman, Shephard, and Creal (2009) proposed to make a sample based estimate of the existence of the moments using generalized Pareto distribution fitted to the tail of the weight distribution. The number of existing moments is less than 1/k (when k>0), where k is the shape parameter of generalized Pareto distribution. Koopman, Shephard, and Creal (2009) focused on making a hypothesis test whether the variance is finite.
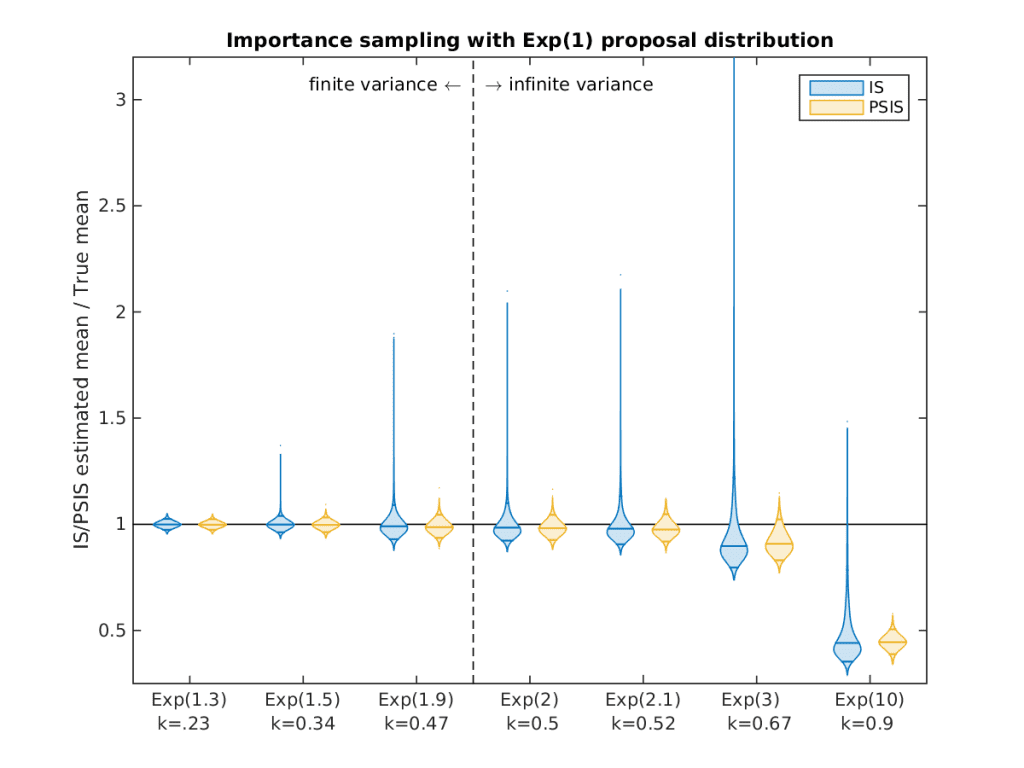
The following figure shows why it is useful to look at the continuous k value, instead of discrete number of moments (and why Pareto smoothing is great). The proposal distribution was Exp(1) and the target distribution was Exp(θ) with varying value of θ. The figure shows results with basic IS (blue) and with Pareto smoothed IS (yellow). The vertical axis is the estimated mean divided by the true mean (ie. values close to 1 are good). The violin plots present the distributions of the results from 1000 repeated simulations (with different random number seeds) using each time 1000 draws from the proposal distribution. For each case the estimated Pareto shape value k is shown.
The figure shows that when the variance is finite the errors are smaller, but the Pareto shape value k gives additional information about the distribution of errors in both finite and infinite variance cases (since we are using a finite number of samples, we don’t in practice observe infinite variance, but it is still a useful concept to describe asymptotic properties). The figure also shows that Pareto smoothing can reduce the error in all cases and that we can get useful estimates also when k≥1/2, although it can’t make miracles when the proposal distribution is too narrow compared to the target distribution. PSIS estimate as described in our paper has allways finite variance, but when k≥1/2 it will have some bias which seems to be small for k<0.7.
Our PSIS-LOO paper with Andrew and Jonah shows one example of the benefit of PSIS and we’ll soon publish other examples where PSIS improves the computation.
Interesting.
The conceptual step from simple direct MC to IS is small as are the problems caused by large weights offering an easier route to grasping Bayesian methods than MCMC.
But I had thought IS (and variations) would not offer a practical alternative to MCMC in the near future.
I’ll need to keep an eye on this work…
IS seems like a natural approach to try in leave-K-out strategies (or in any method that involves small perturbations of a distribution, really).