Jeremy Fox writes:
You’ve probably seen this [by Matthew Hankins]. . . . Everyone else on Twitter already has. It’s a graph of the frequency with which the phrase “marginally significant” occurs in association with different P values. Apparently it’s real data, from a Google Scholar search, though I haven’t tried to replicate the search myself.
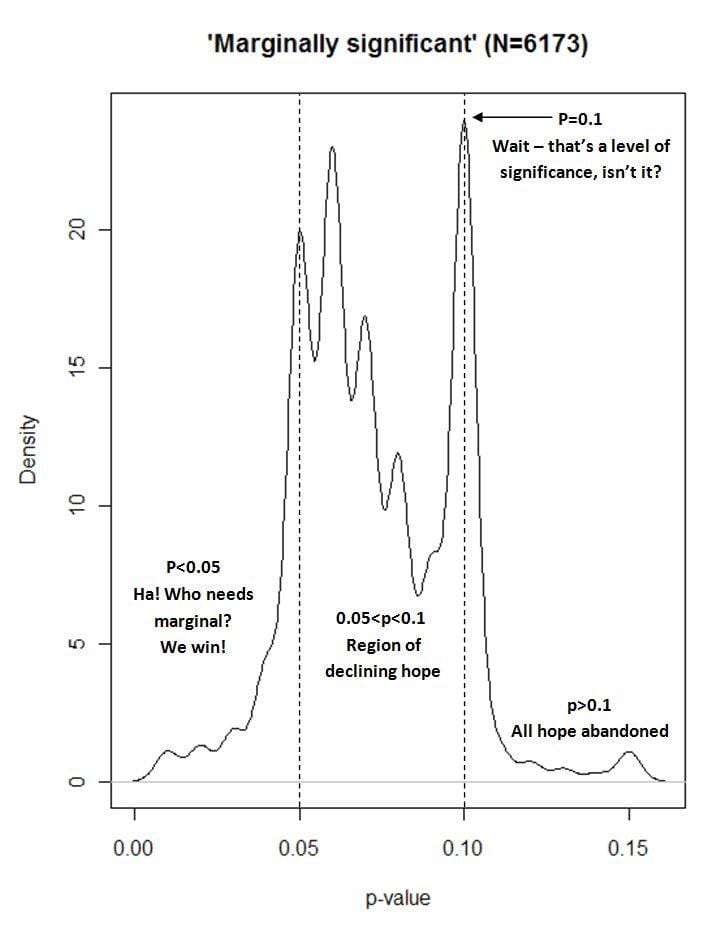
My reply: I admire the effort that went into the data collection and the excellent display (following Bill Cleveland etc., I’d prefer a landscape rather than portrait orientation of the graph, also I’d prefer a gritty histogram rather than a smooth density, and I don’t like the y-axis going below zero, nor do I like the box around the graph, also there’s that weird R default where the axis labels are so far from the actual axes, I don’t know whassup with that . . . but these are all minor, minor issues, certainly I’ve done much worse myself many times even in published articles; see the presentation here for lots of examples), and I used to love this sort of thing, but in my grumpy middle age I’m sort of tired of it.
Let me clarify. I have no problem with Hankins’s graph. It’s excellent. But here’s the thing. In the old days I’d see such a graph (for example, various histograms of published z-scores showing peaks around 2.0 and troughs at 1.95) and think about how researchers can select what results to publish and how they can play around a bit and go from p=0.06 to p=0.04. But after what’s come out in the past few years (most notably, the article by Simmons, Nelson, and Simonsohn; see here for a popular summary of the concerns or here for a bunch of my recent papers on the topic), now I feel the problem is much more serious. A serious researcher can easily get statistical significance when nothing is going on at all (or, of course, when something is going on but where the population comparison of interest is of indeterminate magnitude and direction). And this can happen without the researcher even trying, just from doing an analysis that seems reasonable for the data at hand.
So, given all this, the focus on p=.04 or .06 or .10 seems to be beside the point. It’s worth looking at—again, I applaud what Hankins did—but what it’s focusing on is the least of our problems.
To me, the real problem is binning a number (b = X) into
2 bins: significant and not significant
or 3 bins: significant, marginally or not
As though there were sudden state changes at the boundaries. I would be happy if the unadorned term “significant” was banned in favor of significant(X).
Climate scientists get entangled with this all the time when talking to journalists on things like This case.
Depending on how grumpy you feel, you might enjoy this paper by McCormack et al where they find three topics in medicine where very similar collections of studies got meta-analysed by different authors, arriving at very similar p-values but just either side of 0.05, ending up in wildly different conclusions. Ban this drug! No, wait, put it in the water supply!
Just been bloggin’ about it here, with emphasis on one of the meta-analyses where they found the 95% CI for the hazard ratio going from “0.80 – 0.998” (yes, that’s their own choice of decimal place precisions), then translated that into “0.80-0.99” (errrr…) in the abstract and thence to “apixaban… resulted in lower mortality” (cue ecstatic high pfives in the Pfizer boardroom).
Robert:
Again, these examples are interesting and important, but I want to push against the idea that any particular study has “a p-value.” The trouble is that the p-value depends on the data analysis and the data exclusion and coding rules, which in turn in practice depend on the data.
And one reason that it is not really an appropriate use of Bayesian theorem to condition on a p_value as if it is a known observation.
Also with multiple parameters the type one error rate is a function of the unknown nuisance parameters and I have never been comfortable with maximising over this to get a single convenient number.
I would just like to say that I was enjoying this regularly scheduled “make fun of people who take significance tests as the end-all be-all” session, until I opened my email and saw a new abstract on which I am the 6th-ish author, and it literally reads: “the difference was marginally significant…p=.087”
Sigh. jrc = part of the problem.
If you ever figure out a polite way not to be part of the problem — any problem — when you are sixth author, bottle it and you’ll make a killing.
I OTOH am a bit frustrated by the regularly scheduled “make fun of p-values”: What’s a credible alternative?
1. I don’t want to make fun of p-values. I posted on this graph because someone sent it to me and said that everyone is talking about it. I wanted to explain why, in my view, the problems exposed in this graph are not the central concerns.
2. A better alternative is hierarchical modeling. Instead of snaking through the data and finding one particular comparison that happens to be statistically significant, analyze everything with a big Bayesian model. This is not always so easy to do; in many ways it’s still in the research stage.
Graphs of this kind are actually quite interesting; what they are showing is people respond to incentives. For most researchers the biggest incentive is getting a publication. Whether that statistical significance really means wine drinking reduces heart attacks is a lesser concern. I can see that and hence I’ve no quibble with what this graph shows.
Approach #2 is interesting. I don’t know enough to comment. I do love Bayesian models as part of predictive algorithms, spam filters, classifiers, pattern recognition and applied stuff like that where they are used to achieve a larger, specific goal. Whether they did well or not can be fairly easily benchmarked with quantitative metrics.
What I find hard to use is a Bayesian framework for drawing conclusions or settling answers to questions or judging a model or a hypothesis (the sort of questions where p-values get used often). Somehow the products of the models are hard for me to translate into the answers I’m typically looking for.
Simply stated, a Bayesian analysis calculates the probability of different hypotheses. I find this much easier to traslate into useful answers. Compare the frequentist “The slope is not significantly different from zero (p = 0.10)” with the Bayesian “There is a 78 % probability that that the slope is possitively steeper than zero”.
Rasmus:
The trouble is, I don’t believe that 78% as it comes from a flat prior that I don’t believe. See here for further discussion of this point.
Sorry, should have added “given the model and the prior assumptions”. Though generally, I think the difference between Bayesian and frequentist p-value statistics can be described by that in Bayesian statistics you calculate how probable different hypotheses and parameter values are (given the model and the prior assumptions) and in p-value based statistic you focus instead on how unlikely the data (or rather a summary of the data) is.
In the applied Bayesian papers I’ve seen the conclusion never seems as simple as that.
Rahul,
For me, the biggest problem epistemologically isn’t the use of p-values themselves, its the misuse of p-values as a threshold and as stand-alone justification for inferring the truth (or, in our case, at least titularly, the falsity) of some hypothesis. I interpret p-values as some measure of precision (usually I actually look at standard errors or t-stats, but the same information is (most of the time) carried in the p-value), a measure I tend to mentally inflate to some degree depending on the standard error estimator used. But then I look at how the models are specified and conceive of what variation in the world is being exploited, look at how the data is cut and how sub-groups/covariates are defined, examine all the other estimates in a paper and their relative estimated precision,, look at the theory at hand and ask myself if it makes sense and/or makes other obvious testable predictions that are not investigated, consider my external background knowledge, draw little graphs to myself, and do all the other stuff you do when you are thinking critically.
In short, I look for a paper to make a compelling statistical argument in order to infer the truth. This argument may be imperfect, some estimates less precise than you’d like, some non-trivial questions about identification may remain – but that is the nature of a rhetorical-empirical argument; very few are overwhelmingly compelling on their own. This kind of statistical thinking takes p-values (and standard errors) as important parts of the story, just not the “end-all be-all”.
Precisely. And I agree with you on that.
But I think Andrew’s is a stronger version of a p value criticism I think. And I don’t agree with that.
Rahul asks a good question. What is the credible alternative?
Technical people often consider only 2 main approaches to inference: “frequentist” or Bayesian. However, a lesser known and often superior approach, is called “information theoretic.” The basis for this broad approach is Kullback-Leibler information. This approach is an extension of Fisher’s likelihood and is without the troublesome priors on all the parameters in all the models and all the models themselves.
One can easily compute such things as the likelihood of model i, given the data; evidence ratios (a bit like the Bayes factors) and ways to incorporate model selection uncertainty into estimates of precision. This approach makes a number of ways to make formal inference from all the models in an a prior set (multimodel inference).
I discuss alternatives near the end of my first article linked above.
The real problem here is the lack of appreciation of how P-values relate to evidence and effect size estimation, and it seems to be a problem shared by researchers and statistical blog commenters alike.
I have recently arXived a paper that documents the direct relationship between P-values and likelihood functions, and shows not only the folly of a binary significant/non-significant end point, but also how to ‘see’ the evidence that the P-value represents. http://arxiv.org/abs/1311.0081 Anyone interested in the problem of what to do with P-values should have a look.
I think one could index the likelihood function, as you say, under any one-to-one mapping and have something useful, but it would still rely on the null hypothesis being something worth rejecting, and the likelihood being from a useful model. P-values are not bad things, they just feature heavily in the cookbook statistics that most people who analyse data have learnt.
You are mostly right, but the thing about the likelihood function is that it is not linked to a null hypothesis. Thus if one wishes to form an inference from the likelihood function indexed by the P-value then the inference is not actually affected by the null hypothesis that may have been used to calculate the P-value. Significance testing is in that way akin to estimation, as both Jaynes and Fisher agreed. (And as I demonstrate in the linked paper.)
The cookbook statistics is the biggest problem, as you imply. Why anyone ever thought that it was a good idea to cede the responsibility for inference to an algorithm is beyond me.
I guess it is largely powered by teachers of applied statistics modules (and some students get a single lecture stuffed into their course e.g. medicine in many places) who worry that the students are scared of maths, so seek to reassure them with the cookbook. I see these students all the time and they seem to have been confused more by it, not less. Skip the maths and give them more philosophy of science, that’s my preference.
It was good of you to post this and your intro seems fine to me but … (and I don’t want to seem mean)
Your claim “Student’s t-test for independent samples was chosen
as the exemplar significance test for its ubiquity, and while it is possible that some of the
properties documented will be specific to that test, most will certainly be general.” causes me to lose interest in your paper.
One of the major problems in this are is getting from a likelihood as a function of n parameters to one just involving a single parameter of interest (effect size). The assumptions for the t.test make that dimension reduction almost trivial. Unfortunately that is not the case for almost any other set of assumptions.
It is a very technical area and wiki entry is poor but a start http://en.wikipedia.org/wiki/Likelihood_function#Likelihoods_that_eliminate_nuisance_parameters
I’m sorry that I haven’t solved the insoluble problem for you, and I’m glad to hear that you don’t want to seem mean. However, the main intention of the paper is, as its title and abstract should make clear, to show the relationship between P-values and experimental evidence. The fact that it doesn’t solve your problem with nuisance parameters does not detract from that aspect of my paper. I think that your response _is_ mean. The link to a Wikipedia page is particularly demeaning.
(If the Wikipedia page is poor then you might consider improving it.)
I agree insofar as it’s a little blunt (to say the least) to express one’s personal loss of interest in a paper as though one’s personal interest as a reader should concern the author. I also find the bit about Wikipedia rather patronizing, and echo your encouragement that the critic of the page should take some time with it and responsibility for it (I see from the edit history that this hasn’t happened yet). Still, I get the feeling that the comment was at least intended to be constructive, which ought to exclude it from the “mean” category. Just somewhat blunt and patronizing. By the same token (i.e., my own two cents, nothing more), your response to the comment is a little insincere and defensive…but none of this really matters, does it? Here’s an argument for moving on with what might matter…
I am reading your manuscript as well, and I intend to take more lasting interest in it. However, I too would hope to apply any insights I gain from it to more complex tests than Student’s t (especially multiple regression, and ideally, SEM). Do you really mean to call that an insoluble problem? If your claim that most properties you documented will certainly be general isn’t false (which would detract from the paper somewhat), shouldn’t the problem the commenter raised here be soluble? If so, I’m sure I could use a little help with it too, but I agree you’re entitled to be content with what you’ve contributed, and your responsibility to help us apply it is no greater than the commenter’s responsibility to edit that damned Wikipedia page.
Thank you for the article BTW. I intend to share it with a colleague of mine, with whom I have been debating the possibility that p values would sow less confusion and reinforce fewer misconceptions if they were only reported to be less or greater than the null hypothesis rejection criterion α. He almost had me convinced that this (his proposal) would sacrifice no information of value…so I’ll be eager to see his reaction to your points!
The biggest issue is that P is not a reliable measure. There are plenty of studies where they miss an effect that is really there. There plenty of studies where they find effects that are not there. P is not a good measure.
Check out this great illustration on the dance of the P values.
https://www.google.com/url?sa=t&rct=j&q=dance%20of%20the%20p%20values&source=web&cd=2&ved=0CC4QtwIwAQ&url=http%3A%2F%2Fwww.youtube.com%2Fwatch%3Fv%3D5OL1RqHrZQ8&ei=dfp6UqfZHIvKkAfX04C4Dg&usg=AFQjCNGFHlBgY_MU19YD8DN2uXqQnEPWvw&bvm=bv.55980276,d.eW0
I’ve seen the dance of the P-values before and it is quite impressive. The wide distribution of P-values for a near null effect size is surprising. However, it’s worth noting that the dance of the relevant likelihood function is much less alarming. P-values relate to evidence not by their numerical value but by the likelihood function that they index.
Does anyone know the basic reference for this?
Hope this doesn’t turn out to be a cartoon or a hoax.
I have posted the histogram + link to dataset (Google Docs) here:
https://twitter.com/mc_hankins/status/399492925416955904
Two thoughts:
1) Maybe it’s a problem of naming. Imagine if the two categories were simply called “publishable” and “non-publishable” rather than significant and non-significant. Then, when I said that in my research I’d find a publishable difference, it would carry less of the strong claims about truth that people here seem to be objecting too. Also, if I’d found some publishable differences and was getting an article published, I might take advantage of the opportunity and talk about some fo the almost-publishable differences I’d found in some of the other comparisons.
2) I respect the epistomological issues associated with hypothesis testing, but I think the practical issues will tend to follow us to whatever choice we make for an alternative. The situation is that a large number of practitioners of science have a need for a yes/no cookbook statistical approach that lets them focus on the other aspects of the science. This isn’t a problem just for the statistical part of science. There are lots of people who understand very little about their measurement equipment, and others with an unfortunate grasp on the literature of their field or possibly adjacent relevant fields. Some scientists want to use off-the-shelf analysis tools, and that’s not going to change. In addition, whatever off-the-shelf analysis tool is most widely accepted will tend to be abused to turn almost-publishable results into publishable results. It’s easier to find examples of p values being abused than likelihood ratio tests because the significance tests are more common. If we all suddenly adopted some other criterion for publishability, it would be similarly abused.
Pingback: Friday links: an accidental scientific activist, unkillable birds, the stats of “marginally significant” stats, and more | Dynamic Ecology
Pingback: A week of links - Evolving Economics
Pingback: Marginally significant | Psychologically Flawed