Ratio estimates are common in statistics. In survey sampling, the ratio estimate is when you use y/x to estimate Y/X (using the notation in which x,y are totals of sample measurements and X,Y are population totals).
In textbook sampling examples, the denominator X will be an all-positive variable, something that is easy to measure and is, ideally, close to proportional to Y. For example, X is last year’s sales and Y is this year’s sales, or X is the number of people in a cluster and Y is some count.
Ratio estimation doesn’t work so well if X can be either positive or negative.
More generally we can consider any estimate of a ratio, with no need for a survey sampling context. The problem with estimating Y/X is that the very interpretation of Y/X can change completely if the sign of X changes.
Everything is ok for a point estimate: you get X.hat and Y.hat, you can take the ratio Y.hat/X.hat, no problem. But the inference falls apart if you have enough uncertainty in X.hat that you can’t be sure of its sign.
This problem has been bugging me for a long time, and over the years I’ve encountered various examples in different fields of statistical theory, methods, and applications. Here I’ll mention a few:
– LD50
– Ratio of regression coefficients
– Incremental cost-effectiveness ratio
– Instrumental variables
– Fieller-Creasy problem
LD50
We discuss this in section 3.7 of Bayesian Data Analysis. Consider a logistic regression model, Pr(y=1) = invlogit (a + bx), where x is the dose of a drug given to an animal and y=1 if the animal dies. The LD50 (lethal dose, 50%) is the value x for which Pr(y=1)=0.5. That is, a+bx=0, so x = -a/b. This is the value of x for which the logistic curve goes through 0.5 so there’s a 50% chance of the animal dying.
The problem comes when there is enough uncertainty about b that its sign could be either positive or negative. If so, you get an extremely long-tailed distribution for the LD50, -a/b. How does this happen? Roughly speaking, the estimate for a has a normal dist, the estimate for b has a normal dist, so their ratio has a Cauchy-like dist, in which it can appear possible for the LD50 to take on values such as 100,000 or -300,000 or whatever. In a real example (such as in section 3.7 of BDA), these sorts of extreme values don’t make sense.
The problem is that the LD50 has a completely different interpretation if b>0 than if b<0. If b>0, then x is the point at which any higher dose has a more than 50% chance of killing. If b<0, then any dose lower than x has a more than 50% chance to kill. The interpretation of the model changes completely. LD50 by itself is pretty pointless, if you don’t know whether the curve goes up or down. And values such as LD50=100,000 are pretty meaningless in this case.
Ratio of regression coefficients
Here’s an example. Political science Daniel Drezner pointed to a report by James Gwartney and Robert A. Lawson, who wrote:
Economic freedom is almost 50 times more effective than democracy in restraining nations from going to war. In new research published in this year’s report [2005], Erik Gartzke, a political scientist from Columbia University, compares the impact of economic freedom on peace to that of democracy. When measures of both economic freedom and democracy are included in a statistical study, economic freedom is about 50 times more effective than democracy in diminishing violent conflict. The impact of economic freedom on whether states fight or have a military dispute is highly significant while democracy is not a statistically significant predictor of conflict.
What Gartzke did was run a regression and take the coefficient for economic freedom and divide it by the coefficient for democracy. Now I’m not knocking Gartzke’s work, nor am I trying to make some smug slam on regression. I love regression and have used it for causal inference (or approximate causal inference) in my own work.
My only problem here is that ratio of 50. If beta.hat.1/beta.hat.2=50, you can bet that beta.hat.2 is not statistically significant. And, indeed, if you follow the link to Gartzke’s chapter 2 of this report, you find this:
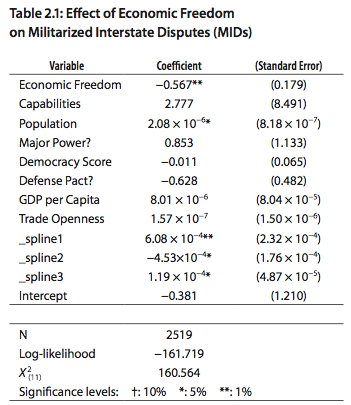
The “almost 50” above is the ratio of the estimates -0.567 and -0.011. (567/11 is actually over 50, but I assume that you get something less than 50 if you keep all the significant figures in the original estimate.) In words, each unit on the economic freedom scale corresponds to a difference of 0.567 on the probability (or, in this case, I assume the logit probability) of a militarized industrial dispute, while a difference of one unit on the democracy score corresponds to a difference of 0.011 on the outcome.
A factor of 50 is a lot, no?
But now look at the standard errors. The coefficient for the democracy score is -0.011 +/- 0.065. So the data are easily consistent with a coefficient of -0.011, or 0.1, or -0.1. All of these are a lot less than 0.567. Even if we put the coef of economic freedom at the low end of its range in absolute value (say, 0.567 – 2*0.179 = 0.2) and put the coef of the democracy score at the high end (say, 0.011 + 2*0.065=0.14)–even then, the ratio is still 1.4, which ain’t nothing. (Economic freedom and democracy score both seem to be defined roughly on a 1-10 scale, so it seems plausible to compare their coefficients directly without transformation.) So, in the context of Gartzke’s statistical and causal model, his data are saying something about the relative importance of the two factors.
But, no, I don’t buy the factor of 50. One way to see the problem is: what if the coef of democracy had been +0.011 instead of -0.011? Given the standard error, this sort of thing could easily have occurred. The implication would be that democracy is associated with more war. Could be possible. Would the statement then be that economic freedom is negative 50 times more effective than democracy in restraining nations from going to war??
Or what if the coef of democracy had been -0.001? Then you could say that economic freedom is 500 times as important as democracy in preventing war.
The problem is purely statistical. The ratio beta.1/beta.2 has a completely different meaning according to the signs of beta.1 and beta.2. Thus, if the sign of the denominator (or, for that matter, the numerator) is uncertain, the ratio is super-noisy and can be close to meaningless.
Incremental cost-effectiveness ratio
Several years ago Dan Heitjan pointed me to some research on the problem of comparing two treatments that can vary on cost and efficacy.
Suppose the old treatment has cost C1 and efficacy E1, and the new treatment has cost C2 and efficacy E2. The incremental cost-effectiveness ratio is (C2-C1)/(E2-E1). In the usual scenario in which cost and efficacy both increase, we want this ratio to be low: the least additional cost per additional unit of efficacy.
Now suppose that C1,E1,C2,E2 are estimated from data, so that your estimated ratio is (C2.hat-C1.hat)/(E2.hat-E1.hat). No problem, right? No problem . . . as long as the signs of C2-C1 and E2-E1 are clear. But suppose the signs are uncertain–that could happen–so that we are not sure whether the new treatment is actually better, or whether it is actually more expensive.
Consider the four quadrants:
1. C2 .gt. C1 and E2 .gt. E1. The new treatment costs more and works better. The incremental cost-effectiveness ratio is positive, and we want it to be low.
2. C2 .gt. C1 and E2 .lt. E1. The new treatment costs more and works worse. The incremental cost-effectiveness ratio is negative, and the new treatment is worse no matter what.
3. C2 .lt. C1 and E2 .gt. E1. The new treatment costs less and works better! The incremental cost-effectiveness ratio is negative, and the new treatment is better no matter what.
4. C2 .lt. C1 and E2 .lt. E1. The new treatment costs less and works worse. The incremental cost-effectiveness ratio is positive, and we want it to be high (that is, a great gain in cost for only a small drop in efficacy).
Consider especially quadrants 1 and 4. An estimate or a confidence interval in incremental cost-effectiveness ratio is meaningless if you don’t know what quadrant you’re in.
Here are the references for this one:
Heitjan, Daniel F., Moskowitz, Alan J. and Whang, William (1999). Bayesian estimation of cost-effectiveness ratios from clinical trials. Health Economics 8, 191-201.
Heitjan, Daniel F., Moskowitz, Alan J. and Whang, William (1999). Problems with interval estimation of the incremental cost-effectiveness ratio. Medical Decision Making 19, 9-15.
Instrumental variables
This is another ratio of regression coefficients. For a weak instrument, the denominator can be so uncertain that its sign could go either way. But if you can’t get the sign right for the instrument, the ratio estimate doesn’t mean anything. So, paradoxically, when you use a more careful procedure to compute uncertainty in an instrumental variables estimate, you can get huge uncertainty estimates that are inappropriate.
Fieller-Creasy problem
This is the name in classical statistics for estimating the ratio of two parameters that are identified with independent normally distributed data. It’s sometimes referred to as the problem as the ratio of two normal means, but I think the above examples are more realistic.
Anyway, the Fieller-Creasy problem is notoriously difficult: how can you get an interval estimate with close to 95% coverage? The problem, again, is that there aren’t really any examples where the ratio has any meaning if the denominator’s sign is uncertain (at least, none that I know of; as always, I’m happy to be educated further by my correspondents). And all the statistical difficulties in inference here come from problems where the denominator’s sign is uncertain.
So I think the Fieller-Creasy problem is a non-problem. Or, more to the point, a problem that there is no point in solving. Which is one reason it’s so hard to solve (recall the folk theorem of statistical computing).
P.S. This all-statistics binge is pretty exhausting! Maybe this one can count as 2 or 3 entries?
Can we simulate the second example like this:
quantile(rnorm(1000,m=-.567,sd=.179)/rnorm(1000,m=-.011,sd=.065))
(and if we cannot, why not?)
If you run it a couple of times, you will see some rather wacky values…
On the ratio of regression coefficients question, why wouldn't you take the ratio of the t-statistics for the two variables as the metric instead of the coefficients? Even though the variables are on the same scale they undoubtedly have very different std devs which, to me at least, makes a direct comparison of the coefficients questionable.
You say Fieller Creasy is difficult – but it's a solved problem. Sure, the intervals come out looking unusual, but they do have the advertised properties.
Moreover, thinking of the intervals as 1D summaries of the underlying 2D problem, they're not particularly weird; just plot an ellipse representing an interval for the 2D parameter.
If the ellipse is far from the y-axis, the slopes of all the lines that pass through both it and the origin is a nice connected set.
If the ellipse is sitting on the y-axis, far from the origin, only lines with very high or low slopes pass through.
If the ellipse is near the origin, any slope is possible.
These are the three cases Fieller Creasy provides.
Otto: Yup.
Thomas: I'm more interested in the coefs as multiplied by typical or interesting changes in the inputs.
Fred: My point is, I don't see why anyone would want these intervals for any practical purpose. To me it seems like a solution to a mathematical problem that is unmoored from the statistical motivation.
An example in finance is the price to earnings ratio (P/E). Price is positive, earnings need not be. Professionals talk about earnings yield (E/P) — problem solved. The popular press sticks with P/E — apparently in the popular imagination earnings are always positive.
I think the software messed up your 4 quadrants under incremental cost-effectiveness ratio. This happens to be a measurement of "return on investment" which is common in business applications.
My workaround is this: if E1-E2 is not statistically significant, then the intervention has no provable benefit, and thus any cost is waste (infinite ratio). (This is wrong because not significant is not the same as no benefit. However, in practice, if E1-E2 is a very small positive number close to 0, the cost effectiveness ratio would be near infinity anyway; and if E1-E2 is a negative number, the intervention had the opposite sign as expected, which means the cost is waste too. In all these cases, the "right" decision would be made.)
I was once asked to calculate a coefficient of variation for a variable measured on the logit scale. Fortunately asking what a negative CV would mean was enough to stop that one.
In practice, I would have thought that having a problem with your sign in an LD50 calculation is telling you that Something is Wrong. It's difficult to imagine an example where you wouldn't a priori expect a positive b. And every good Bayesian can now seen how this helps.
Bob:
I could imagine a positive b in some settings, or a negative b in others, but once you entertain the possibility that it could be positive or negative in any given case, it's hard to avoid thinking about other, non-logistic curves, such as a probability curve that goes up and then down, or down and then up, in which case LD50 is really really meaningless.
P/E ratios can make sense even if E is negative, though the popular press tends to truncate at zero. For instance, when I worked for SpeechWorks during the tail end of the dot com boom, it cost us about $20 to build something we could sell for $10. It was a very repeatable business, with costs going up to match revenue. Somehow, the thinking was that (a) there was some economy of scale that'd eventually kick in, and (b) market share itself is good for sales price.
What also troubled me about the ratio of regression coefficients: I'd surprised if economic freedom and democracy were not positively correlated, potentially introducing a multicollinearity problem and making the ratio very silly. It would be interesting to see the coefficient (and t-stat) on economic freedom in a regression ex-democracy and the coefficient/t-stat on democracy in a regression without the economic freedom variable.
Thomas/Andrew.. Would another approach would be to scale the scores by some function of their std dev? This way, hopefully one would be dealing with similar changes in the variable.
Here is a pretty interesting post about the problems with the 5 percent significance and several variables.
http://sabermetricresearch.blogspot.com/2011/06/f…
@Bob Carpenter: "We lose a little bit on each unit but make it up on volume" ?
Does this call for a simulation approach? Presumably X and Y both have distributions and some correlation assumption can be made. And we can derive interval estimates thus.
You state, "paradoxically, when you use a more careful procedure to compute uncertainty in an instrumental variables estimate, you can get huge uncertainty estimates that are inappropriate."
On instrumental variables, perhaps I misunderstand, but isn't the potential problem when the instrument is weakly correlated with the outcome (after controlling for the predictor of interest), rather than the procedure used to estimate the error on the regression coefficient of the instrument? That is, if you incorrectly underestimate the uncertainty (e.g., by not accounting for clustering in your survey design), your error estimates might be smaller so it looks like there's little uncertainty about the sign of the denominator, but they're wrong.
I like the "30 days of statistics." So far I find it much better than Wegman plagiarism or the musings of a ventilation engineer. Excellent discussion. I recently had to deal with ratios of correlated normals, so I found this discussion both interesting and informative.
I like the 30 days of statistics, too. The Wegman series was getting boring. It came across as the expected ad-hominum against a AGW critic.
Zarkov:
I'm glad the post was useful.
On your other point, be assured that I don't enjoy posting on Wegman! I think plagiarism is horrible, and even more horrible is when the perpetrators don't do the right thing and apologize. I would love for plagiarism in statistics and political science to never exist and then I would never blog on it.
Bill:
See comment to Zarkov above. Beyond this, the blog is free and you can feel free to skip the boring parts!
Those who show off their Latin tags should get them right: ad hominem.
Janet:
I'm no expert on instrumental variables, but I think that things can go wrong if the denominator of the estimate is highly uncertain.
Phil:
Yes, researchers have looked at such things, but in general the literature in that field is pretty unsettled.
Regarding your 2nd point, yes, scaling by sd is what I generally recommend. I was just noting above that Gartzke's unscaled choice seemed reasonable enough given the scales of the variables.
To add on Kaiser's point, while the ICER is still some sort of reference statistics in health economics, often the cost-effectiveness analysis is performed by sort of using a different utility measure. So instead of using the ratio estimator, it is assumed that the utility of an intervention is measured in terms of its net benefit u(e,c) = ke – c, where e=effectiveness; c=costs; k="willingness to pay parameter", which effectively puts costs and effectiveness on the same scale and measures the "cost of an incremental unit of effectiveness".
This formulation is related to the quadrants discussion that Andrew mentioned and I think Kaiser's argument is slightly different from the one used in health economics. In fact, an intervention is evaluated against an available budget, so that rather than just the ICER, what is relevant is whether its value is below some threshold (which happens to be represented by k).
(Incremental) net benefits, i.e. the difference of the utility measures for two interventions is then used for the analysis, with the advantage of being a linear function (rather than a ratio). It has its flaws, but works around the problems associated with ICER.
Seems like negativity is sometimes a red herring. The more fundamental issue is that dividing by a small but uncertain number has undesirable properties. Perhaps rescaling could help. In optics, one often adds a bias to the detector so that photon counts can be symmetrically distributed (it's hard to count a negative photon). Perhaps one could do something like this in these situations (admittedly, I have no idea how).
Joshua:
No, negativity is no red herring. It's fundamental here because the interpretation of the ratio changes completely when the denominator changes sign. The Fieller-Creasy problem etc is typically framed as a difficult inference problem for a well-defined parameter. But really it's the parameter itself that is not meaningful when the denominator can cross the zero boundary.
Gianluca: your formulation is also common in business applications. k would be the maximum dollars the business is willing to pay to acquire an incremental customer. Typically, k is low enough that if the effect is small or the sign is uncertain, it'd be obvious that the intervention would not beat the threshold. This skirts the issue of trying to get good estimates of cost-effectiveness in that zone.
I also think this should be formulated as a math programming problem with two objectives (with shadow prices). In general, I think that should be an active research area: how to take statistically-optimal estimates and use in a math. programming setting in order to optimize real-world objective functions. Is there work in this direction?
Why not just use the delta method, and take the standard error of the ratio?
In computing the standard error using the delta method, you'll end up dividing by the square of a number close to zero, getting an appropriately large standard error and wide confidence interval.
Dan:
No, the problem is that the parameter itself has no meaning if the denominator can change sign. The two signs are two different scenarios, and it makes no sense to make inference for the parameter across the two scenarios.