Howard Wainer writes:
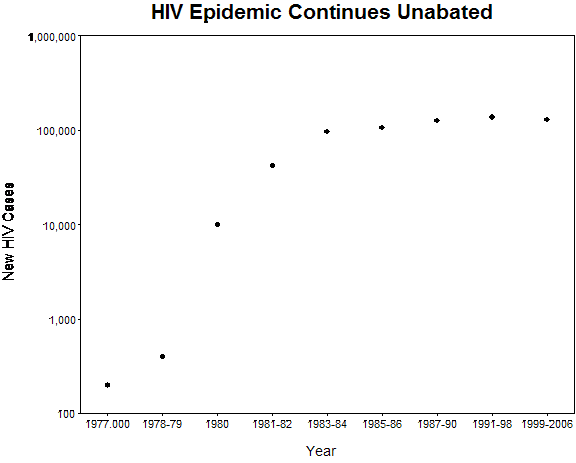
A friend sent me this USA Today article with a graph about HIV:
He sent it because of a paper I published a couple of years ago (with Marc Gessaroli & Monica Verdi) about how we can distort results by changing the bin category boundaries.
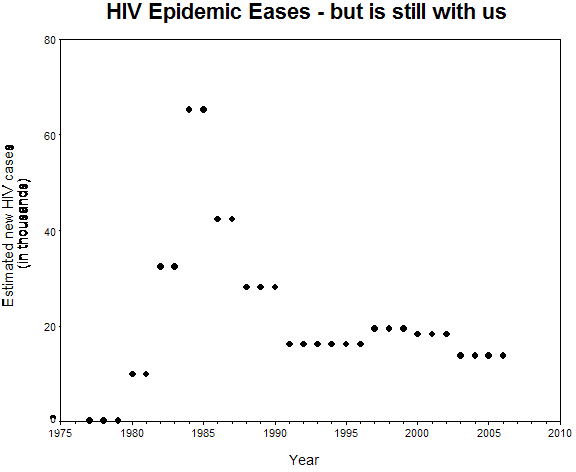
The USA Today graph changes the width of the bins. In the attached alternative plots I tried two tactics. One was to plot the average per year HIV infections for each year in a bin:
The other was to group in such a way as to make a (false) point:
P.S. According to comments below, Howard may have been mistaken in his criticisms. Still an interesting discussion topic, though.

Come, on that's unfair. That second graph isn't misleading, it's pretty much lying. That would be sacrosanct.
While I agree in general about the dangers of miss-binning, I don't think USA Today is nearly as guilty as you are alleging.
Look at the footnote on their chart. The figures are annual averages over the multiyear periods, not totals for the periods. Your graphs are thus wrong, and USA Today's does give a correct interpretation, in this case that HIV infection rates have been stable over the past decade.
The caption states that the numbers are "average annual numbers of infections", meaning that the total number of HIV infections in 2003-6 was 221,600.
As the creator of the original graph (see article Hall, Song, Rhodes et. al. in August 6th issue of JAMA) – I'll just note that 1) the two comments above (Andy McKenzie,Robin Ryder) do have the correct interpretation for the numbers (i.e. cases per year not per bin) , 2) the unequal bin widths were not created by USA Today and 3) a gentle reminder that not every institution (or individual) for whom we may have some disdain will always make the type of mistake that one has primed oneself to detect.
Why bin if you are going to average, anyways? Andrew's point may have missed, but the graphic is a whiff, too. There's no [dependent|independent] variable interpretation. You could have, more clearly binned like:
[1977-1979:600]
[1980-1981:20000]
[1982-1983:64900]
[1984-1985:130400]
[1986-1990:84500]
[1991-1996:48800]
[1997-1999:58400]
[2000-2006:55400]
And we would guess that those numbers were representative of their bins, and that we should be interested in the time frames.
Yeah, but irrespective of the truth in this particular case, the point is that if someone's haphazard about binning — or bins at all — the picture of data they get could be hugely distorted. The last example suggests that it's possible to make any variable dataset say almost anything by being creating about the way it's binned.
This strongly supports the notion that only proper estimation of densities with kernels is the way to treat data like this.