To be honest, I have no idea what this stuff is all about, but it certainly seems important and worth a few dozen Ph.D. theses. Any students around here who can figure this all out and want to explain it to me, I’d be glad to be your advisor, or be on your committee, or whatever. I can’t figure out what’s going on with this one-pixel camera thing but it certainly looks cool.
P.S. Apparently David Dunson’s on the job. Cool.
Andrew,
here is my stab at explaining it:
http://nuit-blanche.blogspot.com/2007/07/how-does…
Igor.
I've been trying to understand this stuff myself. I'm still fuzzy on the differences bettween compressed sensing and other random projection techniques.
Here's my current vague explanation of what's going on; perhaps someone who knows what they're talking about can correct me:
Suppose you have a signal with a single pulse somewhere in it, but you don't know where. To pick up that pulse, you have to measure the signal at every time step, looking for the pulse. This seems wasteful, since just one measurement is necessary to detect it — if only you knew when it was!
But now suppose that you have an instrument which lets you measure the signal in the frequency domain, instead of the time domain, and that furthermore, you can choose which Fourier components to measure — you don't have to sample all frequencies.
A single Fourier component contains information about what the signal is doing at all times. If you sample a few frequencies at random, you can get enough time domain information to localize that single pulse.
Here it's crucial that the frequency domain basis (sinusoids) is incoherent with the time domain pulses (Dirac deltas) ‐ think Heisenberg uncertainty. That's what allows a few Fourier components to contain enough information to localize the mystery pulse. But you also need the original signal to be "sparse": only a few Dirac pulses can be localized if you sample only a few frequency components.
Where I get fuzzy is how you can use the "l1 magic" to do the reconstruction, and how sparsity and incoherence crucially factor into that process.
The advantage is that you don't have to acquire an entire signal and then compress it by tossing out all the "unimportant" components. If your signal is sparse with respect to some basis, and your measuring instrument can sample randomly with respect to a basis incoherent with that one, you can acquire a few samples randomly from the incoherent basis and don't have to bother with all the rest of the data coming in: your sensor can do the compression itself by not bothering to sample any information unnecessary to the reconstruction of the original signal. You don't have to acquire the entire signal, transform it, and then pick out the most important components; random samples will do.
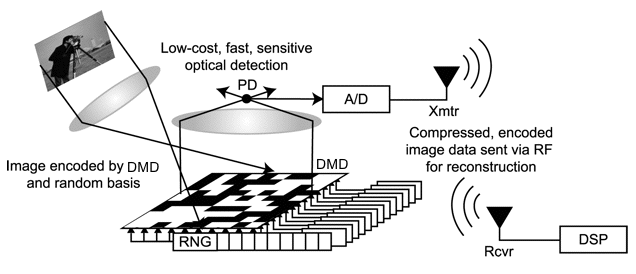
These incoherent measurements are essentially linear combinations of parts of the signal. (Think of the Fourier series, expressing a single Fourier component as a linear combination of time series values.) The Rice "single pixel" camera works by focusing a random combination of image pixels onto the single pixel sensor (using a mirror which can randomly pass or mask light from each pixel), so that the sensor is measuring a random linear combination of all of the image data: it's a mechanical mechanism for acquiring random projections of the signal.
I found terry tao's explanation to be quite useful
NU,
You got it right.
Also:
".. Where I get fuzzy is how you can use the "l1 magic" to do the reconstruction, and how sparsity and incoherence crucially factor into that process…"
Please note the word magic in "l1 magic", it has not escaped people like Candes that this is highly counterintiutive. Roughly speaking,
when given these compressed measurements, and the family of functions on which you think your signal is sparse in, you have to solve for a very underdetermined system, lots of unknowns, few equations. What has been found is that if you use SVD (L2), the solution to that underdetermined system will be sensitive and will not be sparse (most coefficients will be on average close to each other). If on the other hand, you use Linear Programming techniques such as interior methods as developed in the Optimization world, the solution you get is, unexpectedly, not only a solution to L1 (as expected) but also a solution to L0 (L0 norm is the one that counts non zero coefficients) i.e. a solution that is as sparse as possible.
"…I've been trying to understand this stuff myself. I'm still fuzzy on the differences bettween compressed sensing and other random projection techniques.."
As you pointed out, compressed sensing is not about random projections only, you are using the example of the fourier coefficients and the dirac signal which also work (The rice camera can do random projection but it can also do noiselet projection as suggested by Candes and Romberg) So in effect your example is not about random projection. As it stands and because of the good work at Caltech and Berkeley, Compressed sensing with Fourier is currently being investigated by GE and Siemens for rapid insertion into their new lines of MRI machines. But for the case of random projection and how it differs from generic random projections, I would say that my current understanding is that only special random projections can fit because they fulfill this RIP constraint, all others that do not are, let's say not proved to work :-) for the moment and you expect the mathematicians like Tao, Candes and the others who presented and attended the recent Von Neumann conference (http://www.ams.org/meetings/vonneumann07.html ) to lead us to better results (it's a damm shame there is no video of the conference) Imagine yourself in the 1800's watching live how Laplace, Fourier, Legendre are developing the analytical tools you are currently using two hundred years later. Applied math history is in the making as we speak. I think Andrew's estimate is wrong, we are not talking about a few dozen theses on the subject, maybe a few dozen next year at NYU….
Hope this helps,
Igor.