This is Jessica. I previously blogged about conformal prediction, an approach to getting prediction sets that are guaranteed on average to achieve at least some user-defined coverage level (e.g., 95%). If it’s a classification problem, the prediction sets are comprised of a discrete set of labels, and if the outcome is continuous (regression) they are intervals. The basic idea can be described as using a labeled hold-out data set (the calibration set) to adjust the (often wrong) heuristic notion of uncertainty you get from a predictive model, like the softmax value, in order to get valid prediction sets. 

Lately I have been thinking a bit about how useful it is in practice, like when predictions are available to someone making a decision. E.g., if the decision maker is presented with a prediction set rather than just the single maximum likelihood label, in what ways might this change their decision process? It’s also interesting to think about how you get people to understand the differences between a model-agnostic versus a model-dependent prediction set or uncertainty interval, and how use of them should change.

But beyond the human facing aspect, there are some more direct applications of conformal prediction to improve inference tasks. One uses what is essentially conformal prediction to estimate the transfer performance of an ML model trained on one domain when you apply it to a new domain. It’s a useful idea if you’re ok with assuming that the domains have been drawn i.i.d. from some unknown meta-distribution, which seems hard in practice. 

Another recent idea coming from Angelopoulos, Bates, Fannjiang, Jordan, and Zrnic (the first two of whom have created a bunch of useful materials explaining conformal prediction) is in the same spirit as conformal, in that the goal is to use labeled data to “fix” predictions from a model in order to improve upon some classical estimate of uncertainty in an inference. 

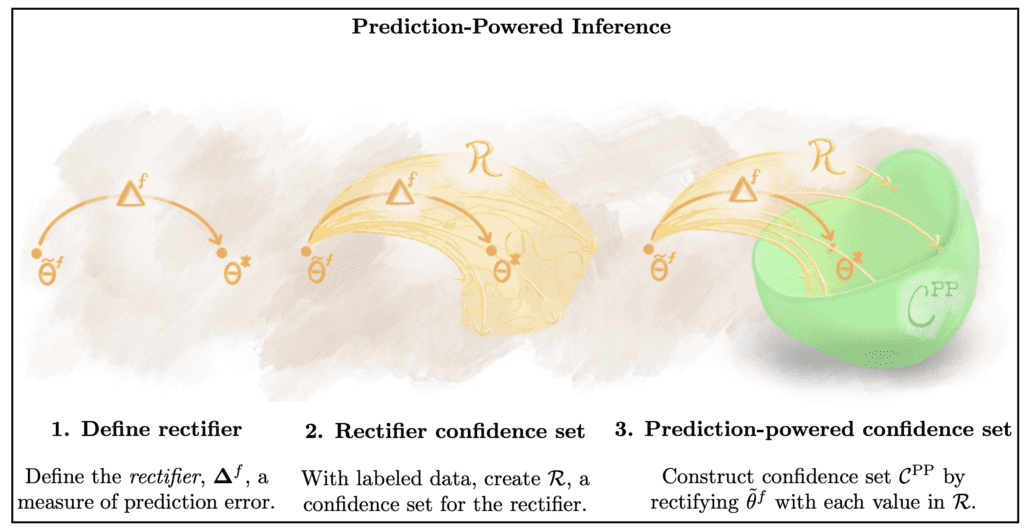
What they call prediction-powered inference is a variation on semi-supervised learning that starts by assuming that you want to estimate some parameter value theta*, and you have some labeled data of size n, a much larger set of unlabeled data of size N >> n, and access to a predictive model that you can apply to the unlabeled data. The predictive model is arbitrary in that it might be fit to some other data than the labeled and unlabeled data you want to use to do inference. The idea is then to first construct an estimate of the error in the predictions of theta* from the model on the unlabeled data. This is called a rectifier since it rectifies the predicted parameter value you would get if we were to treat the model predictions on the unlabeled data as the true/gold standard values in order to recover theta*. Then, you use the labeled data to construct a confidence set estimating your uncertainty about the rectifier. Finally, you use that confidence set to create a provably valid confidence set for theta* which adjusts for the prediction error. 

You can compare this kind of approach to the case where you just construct your confidence set using only the labeled observations, resulting in a wide interval, or where you do inference on the combination of labeled and unlabeled data by assuming the model predicted labels for the unlabeled data are correct, which gets you tighter uncertainty intervals but which may not contain the true parameter value. To give intuition for how prediction powered inference differs, the authors start with an example of mean estimation, where your prediction powered estimate decomposes to your average prediction for the unabeled data, minus the average error in predictions on the labeled data. If the model is accurate, the second term is 0, so you end up with an estimate on the unlabeled data which has much lower variance than your classical estimate (since N >> n). Relative to existing work on estimation with a combination of labeled and unlabeled data, prediction-powered inference assumes that most of the data is unlabeled, and considers cases where the model is trained on separate data, which allows for generalizing the approach to any estimator which is minimizing some convex objective and avoids making assumptions about the model.

Here’s a figure illustrating this process (which is rather beautiful I think, at least by computer science standards):

They apply the approach to a number of examples to create confidence intervals for e.g., the proportion of people voting for each of two candidates in a San Francisco election (using a computer vision model trained on images of ballots), predicting intrinsically disordered regions of protein structures (using AlphaFold), estimating the effects of age and sex on income from census data, etc.

They also provide an extension to cases where there is distribution shift, in the form of the proportion of classes in the labeled being different from that in the unlabeled data. I appreciate this, as one of my pet peeves with much of the ML uncertainty estimation work happening these days is the how comfortably people seem to be using the term “distribution-free,” rather than something like non-parametric, even though the default assumption is that the (unknown) distribution doesn’t change. Of course the distribution matters, using labels that imply we don’t care at all about it feels kind of like implying that there is in fact the possibility of a free lunch.