This is Jessica. Recently I attended part of a workshop on distribution-free uncertainty quantification, which piqued my interest in what machine learning researchers are doing to express uncertainty in prediction accuracy. At one point during a panel Michael Jordan of Berkeley alluded to how uncertainty quantification has long been a niche topic in ML, and still kind of is, but this might be shifting.
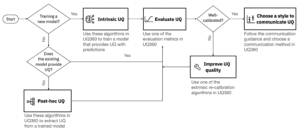
Relatedly, a couple months ago, IBM released a toolkit called Uncertainty Quantification (UQ) 360, with the goal of getting more ML developers to express (and evaluate) uncertainty in model predictions. They imply a high level pipeline where you can start with either a model that provides some (not necessarily valid) uncertainty estimate already, and rely on extrinsic (i.e., post-hoc, distribution-free) uncertainty quantification, or use the toolkit pre-model development and choose a model that provides intrinsic UQ (i.e., uncertainty is intrinsic to the fitting process, like Bayesian neural nets). Either way you then evaluate the UQ you’re getting, and can re-calibrate using the extrinsic approaches.
Conformal prediction, an extrinsic technique that’s been around for awhile but is attracting new interest, came up a fair amount at the workshop. It’s claims are impressively general. Like other currently hot algorithms with strong guarantees, my first impression was that it seemed almost too good to be true. According to a recent tutorial by Angelopoulos and Bates, you can take any old “heuristic notion of uncertainty” from any old model type (or even more generally, any function of X and Y) and use it to create a score where a higher value designates more uncertainty or worse fit between X and Y. You then use the scores from a hold-out sample to generate a statistically valid 1 – alpha confidence interval (prediction region) for continuous outputs or a prediction set (a set of plausible labels with probability 1 – alpha of including the true label) for classification. You need only for instances to be sampled independently from the same (unknown) distribution the model was trained on and the hold-out set was drawn from, or that they are at least exchangeable.
As Angelopoulos and Bates write,
“Critically, the intervals/sets are valid without distributional assumptions or model assumptions, with explicit guarantees with finitely many datapoints. Moreover, they adapt to the difficulty of the input; when the input example is difficult, the uncertainty intervals/sets are large, signaling that the model might be wrong. Without much work, one can use distribution-free methods on any underlying algorithm, such as a neural network, to produce confidence sets guaranteed to contain the ground truth with a user-specified probability, such as 90%. ”
In slightly more detail, the process is to obtain a hold-out set of (ground truth) labeled instances of some size n, look at the distribution of a score derived from some (“possibly uninformative”) heuristic notion of uncertainty output by the model, find the 1 – alpha quantile of the scores for the true labels, slightly adjusted to account for the size of the hold-out set (specifically, the [(n+1)(1-alpha)]/n quantile). Then use that value as a threshold to filter the set of possible outputs (i.e., labels) for some new instance for which ground truth is not known. The remaining set is your prediction set or prediction region, stated to be guaranteed to have probability of obtaining the true label with probability between 1 – alpha and 1 – alpha + 1/(n+1).
So what is the heuristic uncertainty output that allows you to create the distribution of scores? You have to pick one, dependent on the type of model you’re using. However, there appear to be no formal requirements on this score, which is part of what I find unintuitive about conformal prediction.
In a classification context with a neural net, you might start with some form of confidence score provided by a model with a prediction (i.e., the result of applying softmax to the final outputs to create pseudo-probabilities), and then subtract these from 1 to get your score. If your output is continuous, you have various options for the score function, like a standard deviation given some parameter assumptions, variance in the prediction across an ensemble of models, variance given small input perturbations, 0 minus posterior predictive density in your Bayesian model, etc. The authors summarize: “Remarkably, this algorithm gives prediction sets that are guaranteed to provide coverage, no matter what (possibly incorrect) model is used or what the (unknown) distribution of the data is.”
There’s something very Rumpelstiltskin-miller’s-daughter about the whole idea. I went back to look at some of the earlier formulations, credited to Vovk (e.g., this tutorial with Shafer of Dempster-Shafer theory), which formulates the approach for an online setting: “The most novel and valuable feature of conformal prediction is that if the successive examples are sampled independently from the same distribution, then the successive predictions will be right 1 − ε of the time, even though they are based on an accumulating data set rather than on independent data sets.” They explain by connecting the idea to Fisher’s rule for valid prediction intervals (which by the way may have been inspired by eugenics according to the warning label on the paper). However in contrast to Fisher’s desire to use a set of prior observations to create a valid interval for an independently drawn observation for some distribution in a single shot sense, in an online setting where you are making successive predictions (and you have access to features of the new example and the previous examples), the claim is that you can achieve the more powerful, direct guarantee that 95% of the predictions will be correct.
But clearly there’s some dependency on the score function used for these intervals/sets to be helpful. As Angelopoulos and Bates describe, “although the guarantee always holds, the usefulness of the prediction sets is primarily determined by the score function. This should be no surprise— the score function incorporates almost all the information we know about our problem and data, including the underlying model itself.” Shafer and Vovk describe how “The claim of 95% confidence for a 95% conformal prediction region is valid under exchangeability, no matter what the probability distribution the examples follow and no matter what nonconformity measure is used to construct the conformal prediction region. But the efficiency of conformal prediction will depend on the probability distribution and the nonconformity measure. If we think we know the probability distribution, we may choose a nonconformity measure that will be efficient if we are right.”
I guess this isn’t that surprising, in that with non-ML statistical models you don’t expect to learn much from your uncertainty intervals if your model is a poor approximation for the true data generating process, your dataset is limited, etc. So there’s a model debugging process that presumably needs to happen first. It’s a little weird to encounter such strong enthusiastic claims about conformal prediction, when the usefulness in the end still depends heavily on certain choices. Perhaps part of my difficulty finding any of this intuitive is also that I’m so used to thinking of uncertainty in the intrinsic sense, where you care about how much the model has learned and from what.
Going back to IBM’s tool, I like their pipeline perspective as it emphasizes the bigger decision process and implies that evaluating any uncertainty quantification you use is unavoidable. It appears they provide some tools (described here) for thinking about the trade-off between calibration and interval width, though I haven’t dug into it. Also, they have a step for communicating uncertainty, with some guidance! I hadn’t really thought about it before, but I would suspect prediction sets for a classifier are easier for non-technical end-users than intervals on continuous variables, since you don’t have to deal with people’s intuitive expectations of distribution within the interval. For continuous outputs, while the IBM guide is not very detailed, they do at least nod to different possible visualizations, including quantile dotplots and fan charts.
P.S. I’m writing this post as someone who hasn’t studied conformal prediction in much detail, so if I’m mischaracterizing any assumptions in either the online or inductive (hold-out set) setting, someone who knows this work better should speak up!
Woah, that’s cool!
I’m gonna have to read the paper in more detail, but what sort of guarantees does this subset have? You can construct an alpha% confidence/credible set from any part of a space, but people usually want a set of minimal cardinality, that’s non-disjoint, of maximum density, centrally located, or something. And I’m guessing we don’t get individual probabilities, though maybe you can reduce coverage until you filter down to a singleton set to get one good probability?
Still feels a little bit magical to me, but this makes sense. Usually with non parametric statistics the trade off feels like getting lots of variance for a bit more robustness. Stuff like Kolmogorov-Smirnov tests, kaplan-meier survival functions, or bootstrapped confidence intervals are much more dispersed than what you get with hard assumptions, but work ok in internet settings with a million observations a second.
Yes this summary captures the main ideas of conformal prediction. The key observation is that (under the assumption of exchangeability) the rank of the score for a new data point will be uniformly distributed among the ranks of the other data points, from which we can compute and threshold a p-value. The “scores of the other data points” are either the scores of a held-out validation data set (in the inductive case) or the scores from a jack-knife style leave-one-out procedure. Larry Wasserman, Emmanuel Candes, and their collaborators have published several very nice papers applying conformal prediction to produce prediction intervals in a variety of cases, such as quantile regression and functional regression.
More generally, the ML community has become very interested in UQ both for producing calibrated probabilities and for detecting mismatches between the model and post-deployment data (anomaly detection, change-point detection). A particularly interesting problem is the “Open Category” or “Open Set” problem where the post-deployment data in a classification problem includes data points that belong to classes not observed during training. Conformal methods can be applied to set the alarm threshold for anomaly detection to control false alarm rates, but not missed alarm rates.
I co-organized another ICML workshop on Uncertainty in Deep Learning (https://sites.google.com/view/udlworkshop2021/home) that covered many of these issues. This was the third instance of this workshop. More than 100 posters were presented! Step by step, the ML community is studying the issues that statisticians have long known are important. (Or, more accurately, a joint Stat/ML community is exploring these issues within the ML context.)
I was happy to see this post, as I’ve been looking at conformal prediction for a couple of years now. I don’t find it intuitive, and didn’t find this explanation intuitive either! (probably my limitations, not yours). I think the concept is simpler than what you described – it seems to be based on the rank of an observation among the 2 classes (I’ll use 2 classes as its easier to think about), based on the probabilities produced by the ML model. So, if I have an observation that is at the 90th percentile of the probabilities of the class 1 (true) observations, and the 10th percentile of the class 2 (true) observations, then the model is betting pretty heavily on class 1. Subject to your choice of uncertainty threshold, this observation is likely to be predicted to be in class 1, in terms of conformal prediction. The terminology that is used, of a “p-value” I find quite confusing – and unfortunate. My understanding of the p values are that each observation has 2 p values, each representing the relative rank of that observation among the true members of each class. Choosing a significance level amounts to deciding what p values are sufficiently large to warrant predicting membership in that class. Since there are 2 classes and 2 p-values, some observations may be predicted to be in both classes (i.e., uncertain regarding which class), some will be conformally predicted to be on one class or the other, and in some rare cases, might not be predicted to be in either class.
As I said, I have found the concept confusing. If someone can simplify my understanding, that would be appreciated.
I fully acknowledge that my description is probably not very intuitive :-)
I noticed there was some allusion to betting odds/game theory in some of the lit but didn’t dig into it. Did notice the p-value references and also found that confusing.
Hi Dale! Let me try to simplify via example.
Imagine we have K classes. You have an ML classifier that induces an estimated probability distribution over those K classes. The naive thing to do would be to construct a prediction set using these estimated probabilities — rank them from most to least likely, then greedily include them in a prediction set until the total (estimated) mass in the set just exceeds 90%. If the classifier were perfect (i.e., if it perfectly estimated P(Y|X) ), then this set would have exact coverage. (Coverage means that the true class will be in the prediction set with 1-\alpha probability, which you can take to be 90% for now.) But of course, you can’t trust the model’s estimated probabilities. So what do you do?
Conformal prediction provides a fix; the idea is to use the model’s behavior on a small set of fresh data (X_1,Y_1),…,(X_n,Y_n) to faithfully assess the model’s uncertainty. Now, for each pair, look at the model’s estimated probability of the ground truth class—let’s call it s_1, …, s_n for the sake of concreteness. As n grows to infinity, you are guaranteed that 90% of ground truth classes will be above the 10% quantile of the s_i. But because n is not infinite, you need to make a (usually tiny) finite sample correction. This adjusted value, q, is the key to conformal prediction.
Now, when you want to deploy a prediction set on a new X_{n+1}, you feed it into the classifier, and let the prediction set be all classes that have an estimated probability above q. Because of the argument above, this prediction set is guaranteed to contain Y_{n+1} with at least 90% probability.
If you haven’t read through the gentle intro, I would look through it as well. It’s a great place to start.
Feel free to ask further questions, I’m here to answer them.
Hi Dale,
I might be late to enter this discussion now, but I would like to share my attempt to understand conformal prediction. As you mentioned in your comments, some things are not “intuitive” and “the theoretical papers are just too complex”. I had a similar feeling when I started working with conformal prediction. And it was not clear to me from where all this comes. I believe Anastasios Angelopoulos explained the basic idea behind conformal prediction as well as it can be done in a short post. What I want to share, is a notebook where I try to derive the theory behind conformal prediction in a very intuitive and simple, to my understanding, way. By the way, there are no formulas. In the end, I confirm that the constructed predictor is the same as the one generated by an exiting library nonconformist. I think this might be how conformal learning was invented by the authors in the first place.
https://github.com/marharyta-aleksandrova/conformal-learning/blob/main/theory/conformal_learning_from_scratch.ipynb
Hi everybody!
I was really happy to see all of the interest in the ICML Workshop on Distribution-Free Uncertainty Quantification. Many hundreds of people submitted and attended the workshop. I had NO idea that people were so interested in this area beforehand—to me, it was a beautiful moment for the community to band together and show that there’s enough of us to really make an impact together :) Thanks for the shout out.
In my view we are at a point where Distribution-Free methods for UQ are still in their very early stages; we need all sorts of people, from statisticians/mathematicians doing theoretical work to address the limitations of conformal (mainly the marginal coverage property, as Jessica pointed out), to software people building great tools for practitioners.
Perhaps, because DFUQ methods inherit many properties of the base heuristic notion of uncertainty, they should be viewed as more of an “insurance policy” on top of a method that accounts for the more intrinsic aspects of UQ than as a one-size-fits-all solution. Of course, if the model is highly misspecified and gives no conditional information about uncertainty, the marginal guarantee is essentially all you can hope for. At least it’s easy to get with conformal, but it doesn’t solve everything. A lot of work is going into getting closer to conditional guarantees–I’d say that is a main focus of the area currently.
If you have questions about conformal or Distribution-Free stuff, feel free to comment below and I’ll answer, or reach out at [email protected]. I’ll check this thread later today :)
Best,
Anastasios
And I forgot to mention— We are definitely planning on hosting the workshop next year as well :)
It’s gonna be even more fun in person, if possible!!
I’m curious about the language that’s used around conformal prediction intervals. If we were talking about conventional (Neyman-Pearson) 95% CI’s, and we said “the CI contains the true value 95% of the time,” this statement would be false, or at least a shorthand for the truth: the CI actually contains 95% of long-run, independent estimates of the true value. Is that also the case for conformal prediction intervals? Or is there a fundamental difference that makes the statement literally true? If the former, they’re using awfully strong language given that their audience is unlikely to grasp the shorthand. (Granted, statisticians do the same for CI’s, but at least you can look back at the foundational papers on CI’s and find the correct definition.)
Second question: The Fisher rule aside, it appears this approach is not anticipated in conventional statistics; why is that? Is it just that the ML context is fundamentally different from the statistical context, so statisticians never needed a method like this, or have ML theorists just had an insight statisticians have not? My impression is that the answer is the former: conventional statistics is designed to make predictions where the true value remains unknown, whereas conformal prediction relies on the true value of each observation being revealed before the next is observed. However, if there’s a genuinely new insight here, can we reverse-engineer conformal prediction for conventional statistical problems?
+1 on the first point. This is where I am stuck. I found the online formulation slightly clearer about this but I’m still not sure what’s maybe sloppy language in writing for non-experts and what the accepted claim is.
On the second question, not sure, but I did notice Schafer and Vovk conjecture about how, had Fisher thought about it when formulating his notion of a valid prediction interval, he probably would have noticed that despite the dependency between the successive intervals in the online setting, the errors are probabilistically independent. My suspicion is that conventional statistics hasn’t concerned itself with prediction accuracy to the same extent ML has, and when you care primaily about post hoc uncertainty in prediction accuracy, and not about uncertainty in inferred parameter values, you might notice different properties. But that’s just speculation.
As with most (all?) statistical claims, it’s definitely worth understanding, both mathematically and intuitively, exactly what conformal prediction claims. Let’s think about split-conformal (the hold-out set version).
The claim is: if T is the output of a conformal procedure, and (X,Y) is I.I.D. with the holdout data, and then P(Y \in T(X)) >= 1-\alpha. The probability is over everything — X, Y, and T. T is a random function because it was learned from data. So it is really correct to say, on average, that the prediction set contains the true value 90% of the time.
Perhaps the surgeon general’s warning should be bigger. The guarantee is !!!ON AVERAGE!!! — All caps — because you’re allowed to trade off errors in any part of the space to achieve the guarantee. I’m not telling you P(Y \in T(X) | X) >= 1-\alpha — so if X is deterministic, I’m not giving you coverage. I’m telling you that if you sample a new point from the same distribution, I can give you coverage. But in certain parts of X-space, I might do very poorly, and in others, I might over-cover. That is what we mean by average over X. The same is true of Y. If Y are different classes, I am NOT telling you conformal will be class-balanced. I may make all my errors on one class if I want, as long as on AVERAGE, I give you 90% coverage. All of these properties should be queried by somebody seeking to build a good UQ method — See Section 4 of the Gentle Introduction for ways of doing this.
Does this help at all?
Yes, thanks for responding; that was my intuition from reading about it but nice to see it spelled out.
Hi Anastasios, thanks for taking the time to answer these question. I probably don’t understand this well enough to properly formulate my question–my knowledge of this subject is confined to this blog post :)–but do I understand you correctly that this on average guarantee is limited to the actual data set you’re working with, i.e. it doesn’t take into account the bias in this data set in comparison to the superpopulation from which it’s drawn and therefore the guarantee doesn’t necessarily transfer to the superpopulation? (I’m presuming here that the dataset is a random sample of the superpopulation.) Thanks again for helping us to understand this!
No worries, Josh!
Actually, the average guarantee does transfer to the superpopulation in a certain sense.
The “average” is also over the calibration data—meaning any statistical errors that occurred when sampling that dataset are taken into account, and the guarantee is on the data generating distribution (i.e. the superpopulation).
On this same note, there exists a version of conformal that conditions on the calibration data. This is a stronger version, but can require more data. In Section 3.2 of the Gentle Introduction (http://people.eecs.berkeley.edu/~angelopoulos/blog/posts/gentle-intro/), you can take the loss function to be Indicator(Y \notin T(X)) and instead of using Hoeffding’s inequality, use an exact Binomial tail bound. This gives an (alpha,delta)-RCPS with respect to a conformal loss.
Happy to continue discussing—I’ll check this thread later today.
I too am going to speculate similar to Josh.
First, confidence interval coverage is a very weak property (at least on its own) maybe the clearest example being that a “valid” confidence interval (of at least some coverage) can be obtained from a single observation from a N(mu,sigma) even though both mu and sigma are unknown. It is a silly procedure but does have confidence interval coverage and so was published in a statistics journal. Used to be my go to example to deflate the value of just knowing the confidence interval coverage.
Second, I suspect that somewhere a probability distribution is implied that defines what would repeatedly happen given both general assumptions and the empirical data distribution. For instance, in the vanilla bootstrap, the implied probability distribution being that only y values observed have probability and equal to 1/n with multiple samples drawn with replacement. A whole and rather mathematical complicated industry developed to understand bootstrapping and to set out bootstrap procedures that do actually work well in different applications.
It is interesting and worth understanding.
OK right in front of my nose – “if T is the output of a conformal procedure, and (X,Y) is I.I.D. with the holdout data”
So the implied probability model is the empirical distribution of the holdout data?
So if an new (X,Y) is not like a sample from the holdout data, the claim does not apply.
No free lunches or assumption free inferences.
Hi Keith,
Looks like you got it!
1. Actually, there’s an even better trivial valid confidence interval in these settings. Take the prediction set T to be the entire label space with probability 1-alpha, and the null set with probability alpha. Of course, this is a valid and totally useless interval. So, you’re correct that coverage is a weak property. So why is conformal useful?
I would say that the benefit of conformal is that in addition to having valid coverage, it also inherits properties from the underlying heuristic notion of uncertainty. The reality is, in a lot of modern machine learning (deep learning), we don’t have any finite-sample guarantees at all, but the algorithms are nonetheless very performant, and widely deployed. We want to leverage their uncertainty estimates to give us adaptive intervals—conformal lets you do that. At the same time, these algorithms and their build-in notions of uncertainty can be terribly wrong, all the time, and we would never know it. This is where the marginal coverage guarantee gives you an insurance policy. At worst, your intervals will be uninformative — this is only in the case that your underlying heuristic uncertainty was uninformative in the first place, so from the beginning you never had any hope of success.
2. The calibration dataset and the new test point need to be exchangeable. It’s hard to do any statistics at all without a statistical assumption! “Distribution-free” usually refers to not making distributional assumptions—I.e., the distribution of the data can be worst-case or adversarial. However, each data point cannot be deterministically adversarial, which would place you more in the realm of game theory than statistics.
Interesting questions, thanks!
Thanks for your response.
> “Distribution-free” usually refers to not making distributional assumptions
Maybe distribution _form_ free but the distribution of the calibration dataset is a (empirical) distribution.
Not trying to be dismissive of the method but like the bootstrap, its only a good choice if understood and informed choice of the calibration dataset is made for the particular application. And like all choices in statistics, critically assessed as well as it can be.
That is, not used as a black box method for uncertainties about a black box prediction method – https://statmodeling.stat.columbia.edu/2021/06/30/not-being-able-to-say-why-you-see-a-2-doesnt-excuse-your-uninterpretable-model/
Agreed!
> If we were talking about conventional (Neyman-Pearson) 95% CI’s, and we said “the CI contains the true value 95% of the time,” this statement would be false, or at least a shorthand for the truth: the CI actually contains 95% of long-run, independent estimates of the true value.”
False (or unclear). The CI is a random vector Y. The probability that this random vector contains the true value is _at least_ 95% (we’re talking about correct coverage, non-asymptotic CIs, ofc). Probability is nothing else than a normalized measure on the event space, so this absolutely means that 95% of all possible y (realizations of the random vector Y) contain the true value, and it has nothing to do with “long”(?), “short” or “medium” runs of anything. Sure, it doesn’t mean that if I get 100 samples of size N from the data distribution, and I compute the 100 corresponding y, then at least 95 of them will contain the true value. But it does mean that if I consider _all_ the possible samples of size N, and the corresponding y, then 95% of them will contain the true value. In other words, the measure of the set of all ys which contain the true value, divided by the measure of the set of all possible y, is 0.95.
Sure, it has nothing to do with “long-run estimates” when you say “all the possible samples”. One difference is that the latter remains in the ideal realm of random variables while the former has some operational meaning in terms of their realizations.
Which is obviously the only realm where you can give proofs. And BTW, it’s not “all possible samples”, it “all possible samples of finite size N”. There’s a huge difference which does have operational meaning.
Fair point. But what’s the operational meaning if it’s not in terms of having enough observations to make the discussion about random vectors and set measures directly relevant?
When I first looked at conformal prediction it was because I had been using ML models and wanted to see how uncertain (not how accurate, which is the usual measures used – AUC, misclassification rates, etc.) the prediction were. For logistic regression, I could do a bootstrap to obtain confidence intervals for the class probabilities, but I can’t (or don’t know how to) do this for other models, such as neural nets, boosted trees, etc. So, conformal prediction appeared to be a way to do this – subject to your chosen level of significance, it produces predictions that you can say are in one class or the other, or that are too close (i.e., uncertain) to predict.
There is an R package, conformal, which I used – but I didn’t like it much and the last time I looked, it seems to have disappeared. There is now a KNIME implementation which looks much better to me. But the theoretical papers are just too complex for me to follow. Part of the complexity, I believe, is that different scoring functions can be used, so the general literature accommodates this. But most of the implementations I have seen appear to use a simple scoring rule – based on the rank of the classification probabilities relative to the probabilities the model produces for the actual class members.
I’m still trying to get my head around where this approach stands in statistical terms. It makes some intuitive sense, but it seems like it comes out of nowhere.
Perhaps I am associating two unrelated concepts, but I was reading about quantile residuals recently, in the context of GLMs. They were introduced by Dunn/Smyth in https://www.jstor.org/stable/1390802?seq=1#metadata_info_tab_contents and recently expanded upon in the DHARMa package, at https://cran.r-project.org/web/packages/DHARMa/vignettes/DHARMa.html.
I find the concept of what is described in the gentle intro and the DHARMa residuals somewhat similar, except for a few points: In the GLM world we can simulate data based on our model and use that as what as described in the gentle intro paper as the “calibration data”. As opposed to holding out some fresh data. The other main difference is that the quantile for the observed value is calculated, as opposed to a fresh X_{n+1} described here. And then, of course, conformal prediction generates an interval, as opposed to a residual. But it seems either method (Dharma or conformal) could be interchanged, generating a residual or a prediction interval, though I am certainly clueless about the statistical properties of doing so. Just a thought.
I am not so sure that statisticians have been ignoring this issue.
When I was taught pattern recognition out of Aitchison and Dunsmore… forgive my spelling. We where always to told make sure you construct an atypicality index for each prediction in terms of the scoring rule you had developed.
Best
Cps
I only looked at it *very* superficially but broadly it seems to boil down to:
1) You have a model that will produce some output when you feed it some input
2) You have a method to generate a prediction that depends on the output of the model and some parameters
3) You can find the parameters that will get it right with the desired frequency (if it has the right coverage for a known set of random inputs you expect it to have the right coverage for any other set of random inputs)
The model can be a black box, it doesn’t even have to be data-based. You just need it to produce some output like an estimate or a set of labels and scores.
The prediction could be something like an interval [estimate-X estimate+X] or [estimate-A estimate+B] or [estimate/A estimate*B] or “the set of labels with score over S” or “the top T labels” or “the set of top labels with cumulative normalized score over C”.
(I may be wrong!)