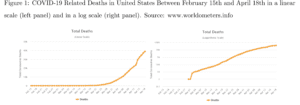
This post may seem like it’s on a six month delay, but actually it’s not! Alexey Guzey sends a link to this blog post about a study done by some researchers at LSE and Yale earlier in pandemic history on how well understood log scales are. They randomly assigned 2000 American adults recruited online to one of the two charts below and then asked them some questions where they estimated the number of new cases for a few different weeks, predicted future cases, and reported their attitudes about different policies, like closing stores or distributing masks. As far as I can tell they didn’t give the participants any instruction about how to read the graphs, other than the text under the title indicating that one was linear scale and one log scaled. Graphs were taken from www.worldometers.info
We show that the scale has important consequences on how people understand and react to the information conveyed. In particular, we find that when people are exposed to a logarithmic scale they have a less accurate understanding of how the pandemic unfolded until now, make less accurate predictions on its future, and have different policy preferences than when they are exposed to a linear scale. This result is consistent with existing evidence that even scientists have trouble understanding information conveyed in logarithmic scale graphs [32]. Since reducing misinformation can help improving the response to COVID-19 [45], mass media and policymakers should present data on the evolution of the pandemic using a graph in a linear scale, or at least they should show both scales.
As they describe in the blog post, only about half as many participants could correctly read the log graph to say which of several weeks had seen more deaths (~40% compared to ~80%). It’s a big difference, though not particularly surprising given that a log scale used for time series is about making it easier to compare growth rates, not absolute numbers.
Somewhat counter to some of the pushback on using log scales for covid graphs, the log scale participants overestimated deaths in the following week by about 10k more on average than the linear scale group had. They also report some weird results where for instance, people who saw linear graphs are less supportive of businesses closing and would wear masks less often. I couldn’t really understand the authors ‘speculation about why this would be. But both of these results suggest it’s not as simple as log scales make people underestimate severity of the pandemic.
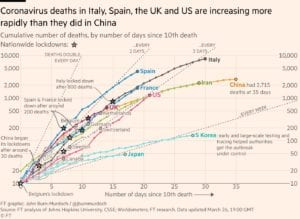
The linear vs log scale for covid outcomes question is something I got asked about often earlier in the pandemic. I don’t really agree with the authors here that log scales should be avoided. For one, they only showed one country on the charts, but many of the covid visualizations people were looking at early on showed multiple time series for different countries or states. The debate about whether log scales are inappropriate seems to hinge on whether you believe we should prioritize the role visualizations can play in crises like these in conveying a metaphor or gist of a situation, which is often by definition imprecise, over the role they have in helping us make more fine-grained comparisons that are also relevant to our situation in ways that text or tables can’t do as well. Comparing how steep two already steep slopes are in a non-log scaled plot is hard. Log scales are simply better for seeing differences in rates to see, e.g., which of several countries is doing a better job of curbing their growth rate. The NYT had a nice article defending log scales back in March 2020, and the Financial Times’ log scaled charts, which many Westerners within a certain demographic have relied on throughout the pandemic, used log scales along with other nice touches like converting the x-axis to days since 10 deaths to account for the different points at which the virus entered different countries, and reference lines to break things into regions so viewers could more easily see when countries had moved from doubling cases ever one to two days to every two to three days, etc.
Log scales being deceiving also came up yesterday in a class I’m teaching. We were talking about “apparent magnitude scaling” which is an idea from cartography that because psychophysics has shown that there is a power law relationship between perceived intensity of a stimulus and its actual intensity, and this can be estimated empirically (the Stevens’s exponent) for that encoding channel (size, lightness, etc.), then it makes sense to adjust the plotted attributes of marks in a visualization so that relative judgments between the marks will be perceived accurately. This idea never really caught on, for some obvious reasons – if some visualizations do this but others don’t, how can we know when it has been adjusted, and does that mean we have to start relying on fine print all the time. One student argued that apparent magnitude scaling was in the same class as log scaling in that you’re distorting what people see. But I don’t think it’s a fair comparison. Apparent magnitude scaling strikes me as more like a crutch that you’re giving people to deal with their deficient perceptual system, which is a good idea in theory but hard to realize. Whereas log scaling is more like a superpower to help them make certain comparisons.
So yeah, let them use log scales, responsibly.
Finally I’m also a little skeptical that seeing more log scaled graphs is going to shape people’s policy attitudes in significant ways the way this paper suggests. There’s been plenty said already about how people’s decisions about how to respond to a pandemic are shaped by factors like where they live or what their political affiliation is. Awhile back I spoke on a panel about visualization for the CDC along with John Burn Murdoch, who has probably received the most flack for his decision to use log scales on the Financial Times covid graphics. At one point he said something along the lines of “people prefer not to see data that conflicts with their preferred covid narrative” in response to a question about hospitalization data, which resonated with me in that it matched the sort of selective resistance to data implying things were getting better (or worse) that I noticed around me early on in the pandemic, even in educated people. The idea that log scales could, for instance, drastically reduce compliance with suggested measures overlooks these other forces, not to mention not being quite as well supported by this paper as some of the conclusions would imply.
Huh. But see also from April 2020: Logarithmic versus Linear Visualizations of COVID-19 Cases Do Not Affect Citizens’ Support for Confinement, https://doi.org/10.1017/S000842392000030X
Jessica:
Regarding “apparent magnitude scaling,” something similar arose in our project on social penumbras. In Figure 2 of that paper, we displayed estimated penumbras using a graph where magnitude was proportional to area. We were aware of the perceptual challenges with such graphs, but we graphed it like that anyway, in part because the concentric-circle pattern of the graph matched the social-science concept we were trying to convey, and in part because it actually worked for us that small areas are still noticeable using that scale.
That PNAS link is giving me access denied but I found your post https://statmodeling.stat.columbia.edu/2021/02/01/social-penumbras-predict-political-attitudes/ (which I had somehow missed when you posted it, but cool paper.) Agree the metaphorical aspect of circular area is nice for it. Seems like this could’ve been a good candidate for rescaling to adjust for perceptual error, since you could at least tell people you did it in the caption.
Those graphs were hard to read! Are all the outer circles the same size? What were the difference groupings on each circle? Is area is even supposed to matter or was I only supposed to pay attention to the radius?
To be fair I only read the caption not the paper, so maybe it’s all obvious if you read the paper (in particular the different groupings is probably explained a million times), but self-contained plots are nice. It’s entirely possible that by constructing the graph this way you are nudging me to read it the right way, but in that case explain the nudge in the caption.
Ben:
When posting images on the blog, I max out the width to 550 pixels to keep a uniform look, but I guess I’m paying the price in that post because, yeah, the tiny font makes it harder to read.
I don’t think the font was the problem. In fact, from the caption I can tell there is interesting information in that graph, but it’s really hard to extract it.
“I only read the caption not the paper…but self-contained plots are nice.”
The parts of a plot should be labeled, but a “self-contained” plot? People make mistakes by quickly scoping the figures and blowing off the text. The text is there for a reason. If it were unnecessary we could just have plots right? :)
Perhaps rather than trying to figure out how to contort plots so that scientists will understand them and know everything they mean by only barely having glanced at them, we could use technology instead to create a product that would force people to read the paper before looking at the plots.
> Perhaps rather than trying to figure out how to contort plots so that scientists will understand them and know everything they mean by only barely having glanced at them
Come on, I know you don’t really believe this :P : https://statmodeling.stat.columbia.edu/2021/02/08/my-thoughts-on-whats-wrong-with-social-science-and-how-to-fix-it-reflections-after-reading-2578-papers/#comment-1704181
I don’t expect to know everything from a single plot, but I think that plot could make a lot more information easy to get at.
> If it were unnecessary we could just have plots right? :)
That would be nice! I’m happy to soften it to “I think it would be worth the time to describe in the caption the unusual plot style and why it is valuable. I believe that you [Andrew] believe this plot should tell me a lot about the paper because you posted it front and center on the post about the paper, rather than the abstract or anything else.”
Of course that whole post was tongue in cheek so maybe I was supposed to be confused.
Puzzled why the vertical scale is not correctly IDd as cumulative deaths and how can one estimate deaths for a given week if the scales are not easily readable. Conceit or sloppiness, but then I am not in this field.
Providing careful and accurate descriptions of the scales on a graph is indeed very important!
The paper in question only shows one graph like this, and it’s not even exponentially increasing – the log version is concave downwards over the range where most of the action is. So it’s not a surprise that it might lead to worse estimates than the linear version.
There should have been a graph that was actually exponentially increasing. On a linear presentation, a steeply rising exponential curve becomes very hard to extrapolate well, presumably because there’s a large perceptual problem in resolving small differences in the upper reaches of the curve.
As to accuracy of estimates, if you present a semilog plot, you can only expect similar fractional errors from one cycle to another. If you translate these to absolute errors, of course there will be a big difference. So how important these errors of judgement will be depends on what you wanted to accomplish be presenting a log version vs a linear version. This doesn’t appear to have been taken into account.
Yep agreed. Visualizations are often intended to support all sorts of comparisons and estimates (and often we do need multiple representations for this reason). To ignore the various tasks for which log scales are clearly better and advise we don’t use them overlooks all this.
Jessica:
Yes, that’s a point worth emphasizing. In many cases where there is one graph, we can do better with two or three. Sure, compactness is a virtue, but when we are writing prose we recognize that sometimes we need to use a few paragraphs to make a point. Similarly, sometimes we need more than one graph.
You might say that sometimes we need a pair of graphs.
+1
In this recent preprint on interactions we discuss scale dependence and assumptions, we positively highlight the OurWorldInData plots, which just do both. Interactive plots, where you can choose between log/linear, per capita/total, comparing countries/just watching one, etc. pp. They facilitate the multiple inferences people might want to make. https://psyarxiv.com/7fm2j/
> Flattening the Curve. Our World in Data (Roser et al., 2020) presents the incidence of people testing positive for SARS-CoV-2 per capita, across countries, in an interactive chart. Viewers can toggle whether they want to see the comparison on a linear or a log-linear scale. The log-linear scale makes it easiest to judge which countries are doing better at flattening the curve, that is, reducing new infections below the numbers expected based on the current number of infected people. We might want to make this comparison if we want to find out whether public health interventions in one country are more effective than in another. However, the linear scale makes it easier to judge which countries are currently worst affected, and makes it easier to see, for instance, which countries will exhaust the number of available intensive care units sooner.
For comparing countries, wouldn’t scaling them all to 100 at the start and then using a linear scale be better than using a log scale?
For covid-type data, I like to scale per-capita. Using an arbitrary max = 100 scale might require some people to feel extra mental effort in understanding, while percap or per million might speak more clearly. (yes, there’s that pesky word “might” again!)
So once again, it depends on the kind of data and what you want to accomplish by showing it.
In the particular case of accumulated covid case counts, for my purposes in comparing countries, I often find it useful to scale to percap *and* to use a log scale. Even better is having the ability to switch between log and linear as easily and quickly as possible.
Also relevant is the more general lack of understanding of logs. When I taught a summer course for high school math teachers, I used the three handouts beginning “log…” at https://web.ma.utexas.edu/users/mks/ProbStatGradTeach/ProbStatGradTeachHome.html .
The teachers seemed to like them, saying that they gained a better understanding of logs and their relevance to science.
Stephen Few had a nice writeup trying to explain logs in commonsense terms: http://www.stephen-few.com/blog/2020/02/21/logarithms-unmuddled/.
This is great! If all viewers of log scaled graphs read this first maybe we wouldn’t need to worry about them. Going to recommend it when I teach journalism students who haven’t always had much stats or math.
As I recall, some research many years ago indicated that a lot of the problem that average people have with thinking about probabilities comes from inability to use fractions. Better to use whole numbers. Now you want them to think about logarithms? Really?
They don’t actually have to think about logarithms, though. The axes are labeled with their parent numbers, not the logarithmic values. Just like someone could use a slide rule for a long time without realizing that the C and D scales are logarithmic. They just have to match the numbers up.
Weber’s law is pretty universal: the representational similarity of numbers in the brain is proportional to their difference on a log scale. This is simply the way magnitudes are actually represented by human (and other primate) minds. Linear scales for things that vary over orders of magnitude are an abomination.