Bill Harris writes:
In “Type M error can explain Weisburd’s Paradox,” you reference Button et al. 2013. While reading that article, I noticed figure 1 and the associated text describing the 50% probability of failing to detect a significant result with a replication of the same size as the original test that was just significant.
At that point, something clicked: what advice do people give for holdout samples, for those who test that way?
R’s Rattle has a default partition of 70/15/15 (percentages). http://people.duke.edu/~rnau/three.htm recommends at least a 20% holdout — 50% if you have a lot of data.
Seen in the light of Button 2013 and Gelman 2016, I wonder if it’s more appropriate to have a small training sample and a larger test or validation sample. That way, one can explore data without too much worry, knowing that a significant number of results could be spurious, but the testing or validation will catch that. With a 70/15/15 or 80/20 split, you risk wasting test subjects by finding potentially good results and then having a large chance of rejecting the result due to sampling error.
My reply:
I’m not so sure about your intuition. Yes, if you hold out 20%, you don’t have a lot of data to be evaluating your model and I agree with you that this is bad news. But usually people do 5-fold cross-validation, right? So, yes you hold out 20%, but you do this 5 times, so ultimately you’re fitting your model to all the data.
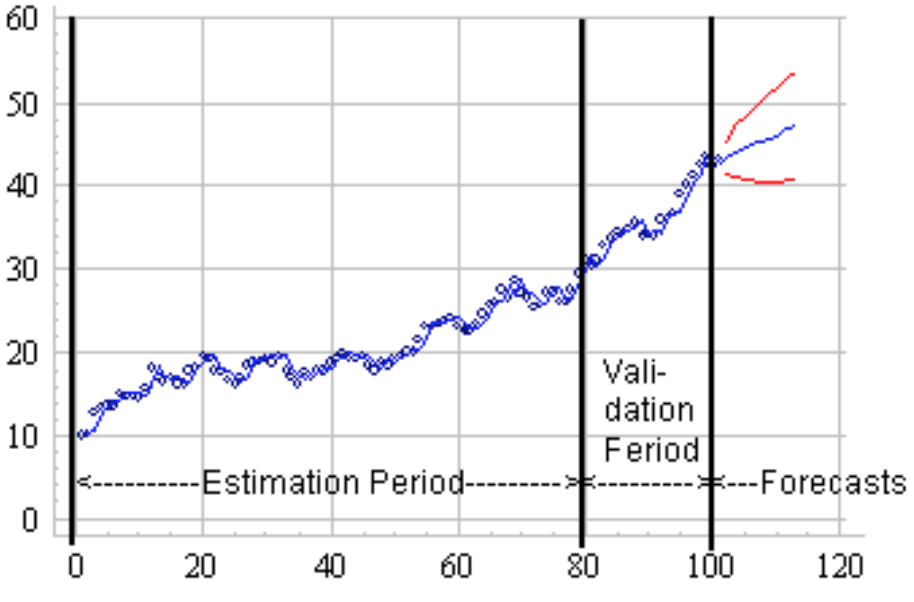
Hmmmm, but I’m clicking on your link and it does seem that people recommend this sort of one-shot validation on a subset (see image above). And this does seem like it would be a problem.
I suppose the most direct way to check this would be to run a big simulation study trying out different proportions for the test/holdout split and seeing what performs best. A lot will depend on how much of the decision making is actually being done at the evaluation-of-the-holdout stage.
I haven’t thought much about this question—I’m more likely to use leave-one-out cross-validation as, for me, I use such methods not for model selection but for estimating the out-of-sample predictive properties of models I’ve already chosen—but maybe others have thought about this.
I’ve felt for awhile (see here and here) that users of cross-validation and out-of-sample testing often seem to forget that these methods have sampling variability of their own. The winner of a cross-validation or external validation competition is just the winner for that particular sample.
P.S. My main emotion, though, when receiving the above email was pleasure or perhaps relief to learn that at least one person is occasionally checking to see what’s new on my published articles page! I hadn’t told anyone about this new paper so it seems that he found it there just by browsing. (And actually I’m not sure of the publication status here: the article was solicited by the journal but then there’ve been some difficulties, we’ve brought in a coauthor . . . who knows what’ll happen. It turns out I really like the article, even though I only wrote it as a response to a request and I’d never heard of Weisburd’s paradox before, but if the Journal of Quantitative Criminology decides it’s too hot for them, I don’t know where I could possibly send it. This happens sometimes in statistics, that an effort in some very specific research area or sub-literature has some interesting general implications. But I can’t see a journal outside of criminology really knowing what to do with this one.)
The graph suggests a related, but perhaps different, question about validation sets. Shouldn’t the decision about appropriate sizes for validation and/or test data sets be different for time series data than more generally? I have commonly seen a recommendation for 50% training data, 30% validation, and 20% testing although I have also seen other recommendations. But I wonder whether the advice should be different for time series data. Depending on the questions to be addressed, it is common to hold out the latest time period of interest – and that is what the graph suggests. But then the issue is not just how large the validation set should be (i.e., how long of a time period), but also whether it should be a contiguous time period or a random selection. Randomly selecting over time would seem to me to be hazardous, unless there is known to be a very stable process. But selecting a contiguous time validation set would seem to amplify the potential for over-fitting or finding spurious patterns. Do you have any advice concerning how to approach this question differently for time series versus cross sectional data?
In time series model error analysis there is an entirely different split to consider called “out of sample.” Out of sample is (usually) different than validation or test because of the sequential nature of the data; basically, in the out of sample set, you don’t update the forecast for a second point based on the actual of a first point; instead, you use the predicted for the first point. The size of the out of sample is dependent on how far out of a forecast you care about.
Hi Andrew,
I might be experiencing some terminological confusion here with regard to names of data subsets (which is not at all uncommon, since different authors use differing definitions of test and validation set). What you’ve written here has gotten me thinking:
“But usually people do 5-fold cross-validation, right? So, yes you hold out 20%, but you do this 5 times, so ultimately you’re fitting your model to all the data. ”
Doesn’t one typically have a holdout set that is used subsequently to the cross-validation procedure as a final check for successful generalization?
I’ll note also that even if you used a holdout set, and if the results were not agreeable, and you then re-optimized your analysis pipeline on the same data, the holdout set’s answer could not be trusted, because you’ve just tuned your algorithm to fit the holdout set. We’ve got a paper about this on bioRXiv, which is intended to help clear the use of terminology in the neuro community especially. Any comments welcome. This is a work in progress.
http://biorxiv.org/content/early/2016/10/03/078816
I remember seeing this awhile back, but never got around to implementing it:
http://www.sciencemag.org/content/349/6248/636.full
IIUC the idea is to *only* look at the overall eval metric for the validation data, never get to see any individual results ( like Kaggle’s public leaderboard). Also, this metric has been modified. If the validation metric is “very close” (which depends on a user-defined threshold plus some random value) to the train metric, return the train metric. Otherwise you return the validation metric + some random noise (they say sampled from a Laplace distribution in the paper but looks like they use normal in the code…).
That may be a misunderstanding though, I would recommend checking the paper.
Initially we thought this could be a good idea, but based on our
experiments there’s limited use for this. We were very disappointed
when we tried to replicate the results. We couldn’t get as good
results by implementing what they describe. It turned out that the
results were made using different algorithm and it’s obvious that have
hand tuned the algorithm parameters carefully to get nice results, and
it seems there’s no way to tune these parameters in practice for new
datasets :(
Aw, poo.
Thanks for sharing your results. That sounds like all too common a story… shame on me for getting excited about something I read in the tabloids I guess.
Yes, the parameters of that synthetic test are hand-tuned and the algorithm slightly different. This is mentioned in the paper (and I know since I’ve designed parts of this test and done the tuning :))
But your assessment misses some basic points:
1. The theoretical analysis in the paper gives results with fundamentally new asymptotic properties but, due to relative complexity does not give constant factors that are usable for reasonably sized applications. Similarly, some aspects of algorithm described in the paper do not seem necessary but appear necessary for the analysis to go through. So we (the authors) had to use a somewhat different algorithm and also puck the parameters manually.
2. The main point of the synthetic test is a proof of concept. We are not making a claim that this test can be easily used to for your typical application. Indeed it is clear to me that applying these results usefully will require a lot of future research and at this point there is no one-size-fits-all application. At the same time, there are already ways to use these ideas in some specific applications. For example, in the context of ML competitions these results are already in (non-public) use.
This is a big problem in Genetics, where we try to compare models based on its ability to predict, from DNA data, *future* unobserved performances (say growth of corn). A problem is that ranking of methods is not robust about how you organise training/validation. Predicting *backwards* (the past) is actually easy, so we do a one-time forward cross-validation, and this is of course subject to lots of noise and idiosyncrasies.
One strategy that we use to palliate the problem is bootstrapping the “holdout sample”, so we get pseudo-replicates:
http://dx.doi.org/10.3168/jds.2013-7745
http://dx.doi.org/10.3168/jds.2015-9360
We’re like in that there are not many outliers around.
As for the size of the data, we put the “training” in the thousands and the “validation” in the hundreds (maybe a 1000-2000). With cut-off date chosen by practicality.
I come across quite frequently people using the most recent year of data as a “hold out”, fit multiple model specifications, and then chose the one that best fits the holdout data (not with cross validation).
In SAS’s automatic forecasting procedures, this is exactly how the “best” model is chosen (assuming a holdout is chosen at all).
I am not a great fan of it, as it amounts to selecting the model based on only the last year of data.
Andrew:
A while back (I can’t think of a good search term at the moment) we had a discussion about experiments and there was an article showing that early adopters (meaning places/organizations) are much more likely to have success than later adopters largely because they are places that the intervention seemed particularly well suited for, which is why they were early adopters or even the pilot site of the intervention. As scale up happens you gradually include more and more places where the ground is less fertile so the effect size goes down. That said, I think the M error is tremendously important and does explain a lot of what people call the scale up problem. But both are happening.
That is to say that I think the Weisburd work on policy interventions is fundamentally different than cross validation even though people might wish that expanding an intervention at one site to ten new sites would be similar to taking a random sample of sites, splitting and then validating the results. It just does not work that way in the real world of finding a research site, perhaps especially a police department, where they will let you do an experiment on a policy intervention. Everyone knows this is true.
Here’s the link http://statmodeling.stat.columbia.edu/2014/08/08/estimated-effect-early-childhood-intervention-downgraded-42-25/#comment-184082
There is also David Draper’s idea of “calibrated cross-validation”
(see http://www.ams.ucsc.edu/~draper/draper-austin-2014-final-version.pdf)
This involves partitioning the data into three sets, M for modeling, V for validation, and C for calibration. M is used to explore plausible models, V to test them, iterating the explore/test process as needed. Then fit the best model (or use Bayesian model averaging) using M and V combined, reporting both inferences from this fit and quality of predictive calibration of this model in C.
If I recall correctly, Breiman et al explore this question in their CART book and decided that 10-fold cross-validation gave a good tradeoff between two sources of variance of the cross-validated estimate (source 1: if k is small in k-fold cross-validation, then the model is fit to a small portion of the data; source 2: if k is large, then the fitted model is evaluated on a small portion of the data). Ronny Kohavi advocated 20 replications of 20-fold cross-validation in his experimental work. Leave-one-out is very noisy and generally is found not to work well.
If you are using a simple holdout set (rather than cross-validation), then the ideal size of the holdout set will depend on the complexity of the model. The model needs to be simple enough that it can be well-fit using a subset of the data, so that there is some data left over for validation. (This is just restating the idea of error degrees of freedom.) With a very complex model, estimation will be hopeless, and holdout validation will make it even more hopeless by reducing the amount of data available for fitting. I don’t see how a “rule of thumb” (such as 70/15/15) can ever make sense for simple holdout.
I agree that a generic rule of thumb may not work. But then what *does* work?
As an applied practitioner, given a black box model, and a certain amount of data what’s a good strategy to choose the split between train-validate-test set sizes?
Tom Dietterich wrote:
> Leave-one-out is very noisy and generally is found not to work well.
Noooo! Tom, you were one of my idols, but then you wrote this. But maybe you are a different Tom Dietterich?
LOO can have high variance if the statistical algorithm A (predictor) is unstable. Example of unstable algorithm is tree model analysed, e.g, by Breiman et al. But if A is stable LOO does not have high variance! See p. 59, Arlot & Celisse (2010). A survey of cross-validation procedures for model selection https://projecteuclid.org/euclid.ssu/1268143839 and references
therein. Many Bayesian models (with full Bayesian inference) are stable. *Generally* I have found LOO to work better than
k-fold-CV. See., LOO vs. K-fold-CV comparison for Bayesian models, e.g. in Vehtari, Gelman and Gabry (2016). Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC. In Statistics and Computing,
doi:10.1007/s11222-016-9696-4. http://arxiv.org/abs/1507.04544. Note that Pareto k diagnostics in PSIS-LOO (see the above mentioned paper) can be used to diagnose stability, that is, if Pareto k values are small, the statistical algorithm (Bayesian model and inference) is stable, and LOO has good properties.
Other discussion here has been mixing ideas for time series and exchangeable data points. In my experience for Bayesian models, LOO is best for exchangeable data points and k-fold-CV is needed for partially exchangeable data points (that is, group structure). This is of course assuming the usual prediction tasks. For time series there are too many choices for the prediction tasks to summaries my recommendations in the time I know have to write this comment, but I can say there is no single rule.
This all falls under the realm of data snooping. Halbert White’s Reality Check which is means of finding bootstrapped confidence intervals on test statistics.In the context of multiple testing, Romano and Wolf derive an asymptotic method for using this to do stepwise testing meanwhile controlling for FWER (i.e., many tests but control over total number of false positives). In a separate paper, Romano-Shaikh-Wolf control for FDR (many tests, controlling for rate of false positives). The methods have been used by economists to determine biases in modeling frameworks and systematic strategies (e.g., Lo-MacKinlay). This has been a relatively rich area of research in econometrics although it seems to have been overlooked entirely by the ‘Financial Charlatanism’ crowd (see irrelevant paper at the end for catchy title).
In some sense, the method is far more binding than LOO, CV, etc, which do not really accommodate for overfitting biases.
Then again, a good rule of thumb works reasonably too.
White: http://www.ssc.wisc.edu/~bhansen/718/White2000.pdf.
Romano-Wolf: http://www.ssc.wisc.edu/~bhansen/718/RomanoWolf2005.pdf
Romano-Shaikh-Wolf: http://www.econ.uzh.ch/dam/jcr:ffffffff-935a-b0d6-ffff-ffffff21355a/et_2008.pdf
Lo-MacKinlay: https://www.researchgate.net/profile/Andrew_Lo/publication/5217236_Data-Snooping_Biases_in_Tests_of_Financial_Asset_Pricing_Models/links/54998be90cf21eb3df60d7b1.pdf
Romano-Wolf (Efficient Computation): http://www.econ.uzh.ch/dam/jcr:3a577acf-6bf1-49aa-af42-01e701625032/stapro_2016.pdf
Corradi-Swanson: http://econweb.rutgers.edu/nswanson/papers/corradi_swanson_whitefest_1108_2011_09_06.pdf
Pseudo-Mathematics and Financial Charlatanism: http://www.ams.org/notices/201405/rnoti-p458.pdf