Usually I (and other statisticians who think a lot about graphics) can’t stand this sort of graph that overloads the y-axis:
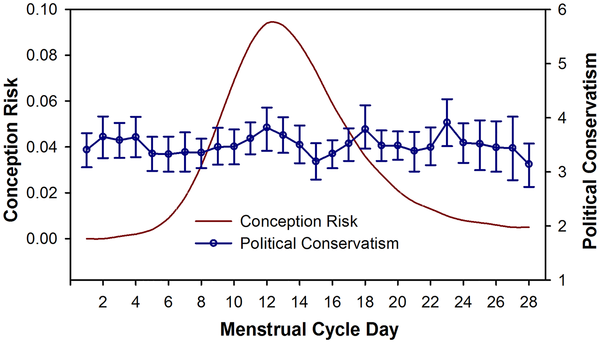
But this example from Isabel Scott and Nicholas Pound actually isn’t so bad at all! The left axis should have a lower bound at 0—it’s not possible for conception risk to be negative—but, other than that, the graph works well.
What’s usually the problem, then? I think the usual problem with double-y-axis graphs is that attention is drawn to the point at which the lines cross.
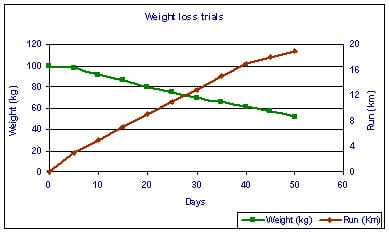
Here’s an example. I was searching the blog for double-y-axis graphs but couldn’t easily find any, so I googled and came across this:
Forget the context and the details—I just picked it out to have a quick example. The point is, when the y-axes are different, the lines could cross anywhere—or they don’t need to cross at all. Also you can make the graph look like whatever you want by scaling the axes.
The top graph above works because the message is that conception risk varies during the monthly cycle while political conservatism doesn’t. It’s still a bit of a cheat—the scale for conception risk just covers the data while for conservatism they use the full 1-6 scale—but, overall, they still get their message across.
I have used them when the point is the direction of the trends rather than their scale. Of course it could be abused (like pairing tiny modulations with major trends), but when it’s reasonable I think it’s reasonable. Here’s a post with two of them: https://familyinequality.wordpress.com/2012/11/26/single-moms-cant-be-scapegoated-for-the-murder-rate-anymore/
Philip:
I think in your examples I’d prefer the connected-dots plot, where you graph one variable on the x-axis and the other on the y-axis, and you connect the points from one year to the next so the time trends are clear. Or I’d just prefer 2 time series, side by side, on separate graphs.
That’s very reasonable. Two graphs side by side with the same units on the x-axis would probably be best. Thanks.
One place double axes plots are useful is multiple units. Say, a heat transfer coefficient in J/m2 C & also in Btu/ft2 F
I think it kind of works because one is an abstract, smoothed distribution and the other is data points .. but it also works because it highlights the discrepancy between the effect size predicted by the “theory” and the observed data. I actually find it helpful for readability to have some space between the axis and the smoothed curve especially since there are no 0 risk days at the aggregate level (there is some woman who is in the fertility window on every number of days since last first day of menses). I think the space is bigger than needed though. Still it gets the information about the lack of variation in the political data across.
Actually, I think the image can be improved upon:
http://myweb.loras.edu/dl526303/RevisedFigure.html
I did not have the data so I had to guesstimate it. I indexed the two scales to the maximum value. This eliminated the fact that the variability of the risk was much larger than the variability of the conservatism measure. What I think is better about this display is that it clearly shows that the only feature common to both is the peak. Outside of that, there is little correlation between the two series and they are often in conflict.
The scales on your y-axes look off.
Both series have been scaled to the maximum value = 1 for that series. I think the scales are correct. The point of re-scaling them to the same scale is to overcome the disparity in the variability of the two measures. The original chart suggests the lack of correlation but, for me, the variability difference overwhelms the rest of the picture. With the same scaling, I think the correlation (or lack thereof) becomes more apparent.
Just for fun, I found a few more with duckduckgo, if you’d care to comment on any them:
http://www.tushar-mehta.com/excel/charts/plot_magnitude_differences.htm
http://www.tushar-mehta.com/excel/charts/0204-single%20graph%20dual%20axis.htm
http://www.mathworks.com/help/matlab/creating_plots/plotting-with-two-y-axes.html
http://www.mathworks.com/help/matlab/creating_plots/graph-with-multiple-x-axes-and-y-axes.html
http://www.statmethods.net/advgraphs/images/axis.png
http://www.ellenfinkelstein.com/pptblog/create-a-powerpoint-chartgraph-with-2-y-axes-and-2-chart-types/
http://www.graphpad.com/guides/prism/6/user-guide/index.htm?graphs_with_two_y_axes.htm
The point is, when the y-axes are different, the lines could cross anywhere—or they don’t need to cross at all.
Unless they are parallel lines, in a 2D world those lines will intersect.