I thought it would be fun to fit a simple model in Stan to estimate the abilities of the teams in the World Cup, then I could post everything here on the blog, the whole story of the analysis from beginning to end, showing the results of spending a couple hours on a data analysis.
It didn’t work so well, but I guess that’s part of the story too.
All the data and code are here.
Act 1: The model, the data, and the fit
My idea was as follows: I’d fit a simple linear item response model, using the score differentials as data (ignoring the shoot-outs). I also have this feeling that when the game is not close the extra goals don’t provide as much information so I’ll fit the model on the square-root scale.
The model is simple: if team i and team j are playing and score y_i and y_j goals, respectively, then the data point for this game is y_ij = sign(y_i-y_j)*sqrt|y_i-y_j|, and the data model is:
y_ij ~ normal(a_i-a_j, sigma_y),
where a_i and a_j are the ability parameters (as they say in psychometrics) for the two teams and sigma_y is a scale parameter estimated from the data. But then before fitting the model I was thinking of occasional outliers such as that Germany-Brazil match so I decided that a t model could make more sense:
y_ij ~ t_df (a_i-a_j, sigma_y),
setting the degrees of freedom to df=7 which has been occasionally recommended as a robust alternative to the normal.
(Bob Carpenter hates this sort of notation because I’m using underbar (_) in two different ways: For y_i, y_j, y_ij, a_i, and a_j, the subscripts represent indexes (in this case, integers between 1 and 32). But for sigma_y, the subscript “y” is a name indicating that this is a scale parameter for the random variable y. Really for complete consistency we should use the notation sigma_”y” to clarify that this subscript is the name, not the value, of a variable.)
[Ed. (Bob again): How about y[i] and y[i,j] for the indexing? Then the notation’s unambiguous. I found the subscripts in Gelman and Hill’s regression book very confusing.]
Getting back to the model . . . There weren’t so many World Cup games so I augmented the dataset by partially pooling the ability parameters toward a prior estimate. I used the well-publicized estimates given by Nate Silver from last month, based on something called the Soccer Power Index. Nate never says exactly how this index is calculated so I can’t go back to the original data, but in any case I’m just trying to do something basic here so I’ll just use the ranking of the 32 teams that he provides in his post, with Brazil at the top (getting a “prior score” of 32) and Australia at the bottom (with a “prior score” of 1). For simplicity in interpretation of the parameters in the model I rescale the prior score to have mean 0 and standard deviation 1/2.
The model for the abilities is then simply,
a_i ~ N(mu + b*prior_score_i, sigma_a).
(I’m using the Stan notation where the second argument to the normal distribution is the scale, not the squared scale. In BDA we use the squared scale as is traditional in statistics.)
Actually, though, all we care about are the relative, not the absolute, team abilities, so we can just set mu=0, so that the model is,
a_i ~ N(b*prior_score_i, sigma_a).
At this point we should probably add weakly informative priors for b, sigma_a, and sigma_y, but I didn’t bother. I can always go back and add these to stabilize the inferences, but 32 teams should be enough to estimate these parameters so I don’t think it will be necessary.
And now I fit the model in Stan, which isn’t hard at all. Here’s the Stan program worldcup.stan:
data {
int nteams;
int ngames;
vector[nteams] prior_score;
int team1[ngames];
int team2[ngames];
vector[ngames] score1;
vector[ngames] score2;
real df;
}
transformed data {
vector[ngames] dif;
vector[ngames] sqrt_dif;
dif <- score1 - score2;
for (i in 1:ngames)
sqrt_dif[i] <- (step(dif[i]) - .5)*sqrt(fabs(dif[i]));
}
parameters {
real b;
real sigma_a;
real sigma_y;
vector[nteams] a;
}
model {
a ~ normal(b*prior_score, sigma_a);
for (i in 1:ngames)
sqrt_dif[i] ~ student_t(df, a[team1[i]]-a[team2[i]], sigma_y);
}
(Sorry all the indentation got lost. I’d really like to display my code and computer output directly but for some reason the *code* tag in html compresses whitespace. So annoying.)
[Ed. (aka, Bob): use the “pre” tag rather than the “code” tag. I just fixed it for this blog post.]
I didn’t get the model working right away—I had a few typos and conceptual errors (mostly dealing with the signed square root), which I discovered via running the model, putting in print statements, checking results, etc. The above is what I ended up with. The whole process of writing the model and fixing it up took 20 minutes, maybe?
And here’s the R script:
library("rstan")
teams <- as.vector(unlist(read.table("soccerpowerindex.txt", header=FALSE)))
nteams <- length(teams)
prior_score <- rev(1:nteams)
prior_score <- (prior_score - mean(prior_score))/(2*sd(prior_score))
data2012 <- read.table ("worldcup2012.txt", header=FALSE)
ngames <- nrow (data2012)
team1 <- match (as.vector(data2012[[1]]), teams)
score1 <- as.vector(data2012[[2]])
team2 <- match (as.vector(data2012[[3]]), teams)
score2 <- as.vector(data2012[[4]])
df <- 7
data <- c("nteams","ngames","team1","score1","team2","score2","prior_score","df")
fit <- stan_run("worldcup.stan", data=data, chains=4, iter=2000)
print(fit)
(I'm using stan_run() which is a convenient function from Sebastian that saves the compiled model and checks for it so I don't need to recompile each time. We're planning to incorporate this, and much more along these lines, into rstan 3.)
This model fits ok and gives reasonable estimates:
Inference for Stan model: worldcup.
4 chains, each with iter=2000; warmup=1000; thin=1;
post-warmup draws per chain=1000, total post-warmup draws=4000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
b 0.46 0.00 0.10 0.26 0.40 0.46 0.53 0.66 1292 1
sigma_a 0.15 0.00 0.06 0.05 0.10 0.14 0.19 0.29 267 1
sigma_y 0.42 0.00 0.05 0.33 0.38 0.41 0.45 0.53 1188 1
a[1] 0.35 0.00 0.13 0.08 0.27 0.36 0.44 0.59 4000 1
a[2] 0.39 0.00 0.12 0.16 0.32 0.39 0.47 0.66 4000 1
a[3] 0.44 0.00 0.14 0.19 0.34 0.43 0.53 0.74 1101 1
a[4] 0.19 0.00 0.17 -0.19 0.10 0.22 0.31 0.47 1146 1
a[5] 0.29 0.00 0.14 0.02 0.20 0.29 0.37 0.56 4000 1
a[6] 0.30 0.00 0.13 0.06 0.22 0.29 0.37 0.56 4000 1
a[7] 0.33 0.00 0.13 0.09 0.24 0.32 0.41 0.62 1327 1
a[8] 0.16 0.00 0.14 -0.16 0.08 0.17 0.25 0.41 4000 1
a[9] 0.06 0.00 0.15 -0.29 -0.03 0.08 0.16 0.32 1001 1
a[10] 0.20 0.00 0.12 -0.02 0.12 0.19 0.27 0.46 4000 1
a[11] 0.27 0.01 0.14 0.04 0.17 0.25 0.36 0.58 746 1
a[12] 0.06 0.00 0.14 -0.23 -0.01 0.07 0.14 0.33 4000 1
a[13] 0.06 0.00 0.13 -0.21 -0.02 0.06 0.14 0.31 4000 1
a[14] 0.03 0.00 0.13 -0.26 -0.05 0.04 0.11 0.29 4000 1
a[15] -0.02 0.00 0.14 -0.31 -0.09 -0.01 0.07 0.24 4000 1
a[16] -0.06 0.00 0.14 -0.36 -0.14 -0.05 0.03 0.18 4000 1
a[17] -0.05 0.00 0.13 -0.33 -0.13 -0.04 0.03 0.21 4000 1
a[18] 0.00 0.00 0.13 -0.25 -0.08 -0.01 0.07 0.27 4000 1
a[19] -0.04 0.00 0.13 -0.28 -0.11 -0.04 0.04 0.22 4000 1
a[20] 0.00 0.00 0.13 -0.24 -0.09 -0.02 0.08 0.29 1431 1
a[21] -0.14 0.00 0.14 -0.43 -0.22 -0.14 -0.06 0.14 4000 1
a[22] -0.13 0.00 0.13 -0.37 -0.21 -0.13 -0.05 0.15 4000 1
a[23] -0.17 0.00 0.13 -0.45 -0.25 -0.17 -0.09 0.09 4000 1
a[24] -0.16 0.00 0.13 -0.40 -0.24 -0.16 -0.08 0.12 4000 1
a[25] -0.26 0.00 0.14 -0.56 -0.34 -0.25 -0.17 0.01 4000 1
a[26] -0.06 0.01 0.16 -0.31 -0.17 -0.08 0.05 0.28 658 1
a[27] -0.30 0.00 0.14 -0.59 -0.38 -0.29 -0.21 -0.03 4000 1
a[28] -0.39 0.00 0.15 -0.72 -0.48 -0.38 -0.29 -0.12 1294 1
a[29] -0.30 0.00 0.14 -0.57 -0.39 -0.31 -0.22 -0.02 4000 1
a[30] -0.41 0.00 0.14 -0.72 -0.50 -0.40 -0.32 -0.16 1641 1
a[31] -0.25 0.00 0.15 -0.50 -0.35 -0.27 -0.15 0.08 937 1
a[32] -0.40 0.00 0.14 -0.69 -0.48 -0.39 -0.31 -0.13 4000 1
lp__ 64.42 0.86 12.06 44.83 56.13 62.52 71.09 93.28 196 1
Really, 2000 iterations are overkill. I have to get out of the habit of running so long straight out of the box. In this case it doesn't matter---it took about 3 seconds to do all 4 chains---but in general it makes sense to start with a smaller number such as 100 which is still long enough to reveal major problems.
In any case, with hierarchical models it's better general practice to use the Matt trick so I recode the model as worldcup_matt.stan, which looks just like the model above except for the following:
parameters {
real b;
real sigma_a;
real sigma_y;
vector[nteams] eta_a;
}
transformed parameters {
vector[nteams] a;
a <- b*prior_score + sigma_a*eta_a;
}
model {
eta_a ~ normal(0,1);
for (i in 1:ngames)
sqrt_dif[i] ~ student_t(df, a[team1[i]]-a[team2[i]], sigma_y);
}
We fit this in R:
fit <- stan_run("worldcup_matt.stan", data=data, chains=4, iter=100)
print(fit)
And here's what we get:
Inference for Stan model: worldcup_matt.
4 chains, each with iter=100; warmup=50; thin=1;
post-warmup draws per chain=50, total post-warmup draws=200.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
b 0.46 0.01 0.10 0.27 0.39 0.45 0.53 0.65 200 1.01
sigma_a 0.13 0.01 0.07 0.01 0.08 0.13 0.18 0.28 55 1.05
sigma_y 0.43 0.00 0.05 0.35 0.38 0.42 0.46 0.54 136 0.99
eta_a[1] -0.24 0.07 0.92 -1.90 -0.89 -0.23 0.35 1.81 200 0.99
eta_a[2] 0.10 0.06 0.83 -1.48 -0.32 0.17 0.65 1.52 200 1.00
eta_a[3] 0.55 0.06 0.82 -0.99 0.00 0.55 1.08 2.06 200 1.00
eta_a[4] -0.54 0.08 1.10 -2.36 -1.33 -0.58 0.18 1.61 200 1.01
eta_a[5] 0.05 0.07 0.99 -1.64 -0.68 0.05 0.70 1.80 200 0.99
eta_a[6] 0.18 0.06 0.79 -1.36 -0.32 0.17 0.75 1.51 200 0.99
eta_a[7] 0.52 0.07 0.94 -1.30 -0.05 0.62 1.10 2.25 200 0.98
eta_a[8] -0.27 0.06 0.89 -1.84 -0.95 -0.26 0.36 1.45 200 0.98
eta_a[9] -0.72 0.06 0.79 -2.25 -1.28 -0.74 -0.17 0.82 200 0.99
eta_a[10] 0.18 0.06 0.86 -1.60 -0.38 0.21 0.81 1.78 200 0.99
eta_a[11] 0.71 0.06 0.90 -0.98 0.08 0.79 1.29 2.54 200 1.00
eta_a[12] -0.39 0.06 0.89 -2.16 -0.97 -0.36 0.19 1.27 200 0.99
eta_a[13] -0.18 0.06 0.90 -1.77 -0.78 -0.18 0.44 1.55 200 1.00
eta_a[14] -0.25 0.06 0.90 -1.86 -0.87 -0.28 0.32 1.52 200 0.99
eta_a[15] -0.33 0.07 0.99 -2.27 -1.06 -0.33 0.42 1.58 200 0.99
eta_a[16] -0.43 0.06 0.83 -1.78 -1.06 -0.50 0.22 1.13 200 1.00
eta_a[17] -0.16 0.07 0.94 -1.90 -0.84 -0.20 0.51 1.65 200 0.98
eta_a[18] 0.18 0.05 0.76 -1.20 -0.28 0.10 0.69 1.59 200 0.99
eta_a[19] 0.12 0.07 0.94 -1.63 -0.47 0.07 0.73 2.10 200 1.00
eta_a[20] 0.41 0.07 0.92 -1.47 -0.24 0.40 0.90 2.19 200 1.01
eta_a[21] -0.08 0.06 0.85 -1.58 -0.68 -0.10 0.49 1.58 200 0.98
eta_a[22] 0.03 0.06 0.82 -1.58 -0.58 0.05 0.58 1.55 200 1.00
eta_a[23] -0.12 0.06 0.83 -1.86 -0.58 -0.14 0.49 1.40 200 0.99
eta_a[24] 0.11 0.07 0.94 -1.62 -0.54 0.12 0.78 1.91 200 0.99
eta_a[25] -0.25 0.07 1.01 -2.09 -0.94 -0.27 0.37 1.99 200 0.99
eta_a[26] 0.98 0.07 0.97 -0.99 0.37 1.04 1.61 2.87 200 1.00
eta_a[27] -0.14 0.07 0.97 -2.05 -0.79 -0.16 0.55 1.78 200 0.98
eta_a[28] -0.61 0.07 0.99 -2.95 -1.20 -0.53 0.05 1.18 200 0.99
eta_a[29] 0.07 0.06 0.89 -1.55 -0.46 0.09 0.64 1.84 200 0.99
eta_a[30] -0.38 0.06 0.89 -1.95 -1.05 -0.37 0.25 1.38 200 1.00
eta_a[31] 0.65 0.07 0.92 -1.22 0.01 0.76 1.35 2.26 200 1.00
eta_a[32] -0.09 0.06 0.81 -1.72 -0.61 -0.12 0.46 1.36 200 0.99
a[1] 0.35 0.01 0.13 0.09 0.27 0.35 0.42 0.59 200 1.00
a[2] 0.38 0.01 0.11 0.16 0.30 0.38 0.44 0.59 200 1.00
a[3] 0.42 0.01 0.14 0.20 0.33 0.39 0.48 0.73 154 1.01
a[4] 0.21 0.01 0.19 -0.22 0.12 0.25 0.33 0.51 200 1.02
a[5] 0.28 0.01 0.14 0.03 0.20 0.29 0.36 0.59 200 0.99
a[6] 0.29 0.01 0.12 0.07 0.21 0.28 0.36 0.51 200 0.99
a[7] 0.32 0.01 0.15 0.08 0.22 0.30 0.40 0.63 200 0.99
a[8] 0.17 0.01 0.13 -0.13 0.08 0.18 0.24 0.39 200 0.99
a[9] 0.08 0.01 0.12 -0.21 0.01 0.09 0.16 0.28 161 1.00
a[10] 0.19 0.01 0.11 -0.06 0.12 0.18 0.24 0.45 200 0.99
a[11] 0.25 0.01 0.14 0.04 0.15 0.22 0.33 0.61 94 1.02
a[12] 0.05 0.01 0.13 -0.26 -0.02 0.07 0.13 0.26 200 1.00
a[13] 0.06 0.01 0.12 -0.20 -0.01 0.07 0.13 0.26 200 0.99
a[14] 0.03 0.01 0.12 -0.21 -0.03 0.04 0.09 0.31 200 1.00
a[15] -0.02 0.01 0.13 -0.32 -0.10 0.00 0.07 0.20 200 0.99
a[16] -0.05 0.01 0.12 -0.31 -0.12 -0.04 0.03 0.14 200 1.00
a[17] -0.04 0.01 0.14 -0.32 -0.11 -0.02 0.04 0.22 200 0.98
a[18] -0.01 0.01 0.11 -0.22 -0.07 -0.03 0.04 0.26 200 0.99
a[19] -0.04 0.01 0.13 -0.31 -0.12 -0.05 0.01 0.24 200 1.01
a[20] -0.02 0.01 0.14 -0.26 -0.10 -0.04 0.05 0.35 200 1.01
a[21] -0.13 0.01 0.12 -0.38 -0.20 -0.12 -0.05 0.10 200 0.99
a[22] -0.13 0.01 0.12 -0.35 -0.20 -0.13 -0.06 0.10 200 1.00
a[23] -0.18 0.01 0.13 -0.44 -0.24 -0.17 -0.11 0.03 200 1.00
a[24] -0.17 0.01 0.13 -0.41 -0.25 -0.18 -0.09 0.07 200 1.00
a[25] -0.25 0.01 0.13 -0.51 -0.33 -0.24 -0.16 -0.02 200 0.99
a[26] -0.08 0.02 0.17 -0.33 -0.20 -0.11 0.02 0.29 82 1.02
a[27] -0.29 0.01 0.14 -0.54 -0.36 -0.28 -0.19 -0.06 200 0.98
a[28] -0.37 0.01 0.16 -0.81 -0.46 -0.35 -0.27 -0.11 200 1.00
a[29] -0.29 0.01 0.12 -0.55 -0.38 -0.30 -0.23 -0.05 200 0.99
a[30] -0.39 0.01 0.14 -0.71 -0.47 -0.38 -0.29 -0.17 180 1.00
a[31] -0.25 0.01 0.15 -0.47 -0.36 -0.27 -0.17 0.06 200 1.01
a[32] -0.40 0.01 0.14 -0.69 -0.48 -0.40 -0.31 -0.14 200 1.00
lp__ -1.06 0.94 5.57 -12.58 -4.46 -0.73 2.64 9.97 35 1.08
All this output isn't so bad: the etas are the team-level residuals and the a's are team abilities. The group-level error sd sigma_a is estimated at 0.13 which is a small value, which indicates that, unsurprisingly, our final estimates of team abilities are not far from the initial ranking. We can attribute this to a combination of two factors: first, the initial ranking is pretty accurate; second, there aren't a lot of data points here (indeed, half the teams only played three games each) so it would barely be possible for there to be big changes.
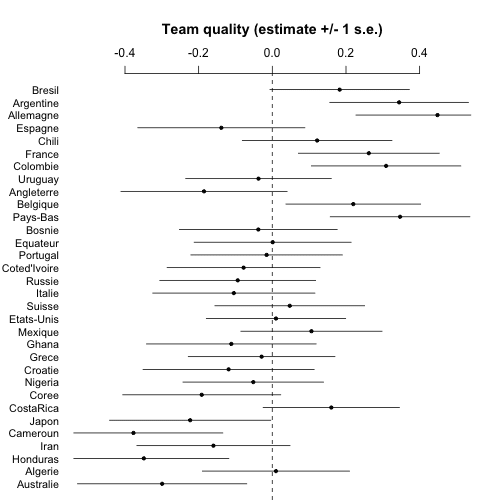
Now it's time to make some graphs. First a simple list of estimates and standard errors of team abilities. I'll order the teams based on Nate's prior ranking, which makes sense for a couple reasons. First, this ordering is informative, there's a general trend from good to bad so it should be easy to understand the results. Second, the prior ranking is what we were using to pull toward in the multilevel model, so this graph is equivalent to a plot of estimate vs. group-level predictor, which is the sort of graph I like to make to understand what the multilevel model is doing.
Here's the code:
colVars <- function(a) {n <- dim(a)[[1]]; c <- dim(a)[[2]]; return(.colMeans(((a - matrix(.colMeans(a, n, c), nrow = n, ncol = c, byrow = TRUE)) ^ 2), n, c) * n / (n - 1))}
sims <- extract(fit)
a_sims <- sims$a
a_hat <- colMeans(a_sims)
a_se <- sqrt(colVars(a_sims))
library ("arm")
png ("worldcup1.png", height=500, width=500)
coefplot (rev(a_hat), rev(a_se), CI=1, varnames=rev(teams), main="Team quality (estimate +/- 1 s.e.)\n", cex.var=.9, mar=c(0,4,5.1,2), xlim=c(-.5,.5))
dev.off()
And here's the graph:
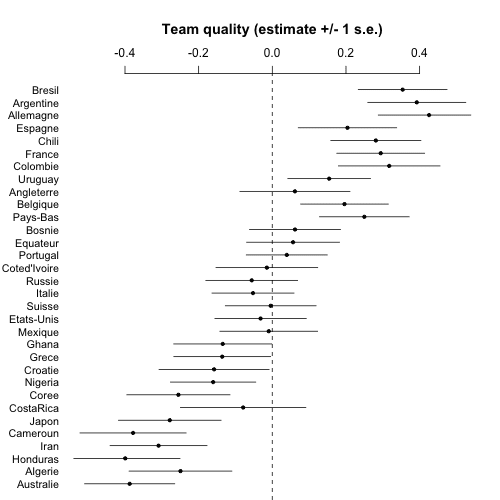
At this point we could compute lots of fun things such as the probability that Argentina will beat Germany in the final, etc., but it's clear enough from this picture that the estimate will be close to 50% so really the model isn't giving us anything for this one game. I mean, sure, I could compute such a probability and put it in the headline above, and maybe get some clicks, but what's the point?
One thing I am curious about, though, is how much of these estimates are coming from the prior ranking? So I refit the model. First I create a new Stan model, "worldcup_noprior_matt.stan", just removing the parameter "b". Then I run it from R:
fit_noprior <- stan_run("worldcup_noprior_matt.stan", data=data, chains=4, iter=100)
print(fit_noprior)
Convergence after 100 iterations is not perfect---no surprise, given that with less information available, the model fit is less stable---so I brute-force it and run 1000:
fit_noprior <- stan_run("worldcup_noprior_matt.stan", data=data, chains=4, iter=1000)
print(fit_noprior)
Now time for the plot. I could just copy the above code but this is starting to get messy so I encapsulate it into a function and run it:
worldcup_plot <- function (fit, file.png){
sims <- extract(fit)
a_sims <- sims$a
a_hat <- colMeans(a_sims)
a_se <- sqrt(colVars(a_sims))
library ("arm")
png (file.png, height=500, width=500)
coefplot (rev(a_hat), rev(a_se), CI=1, varnames=rev(teams), main="Team quality (estimate +/- 1 s.e.)\n", cex.var=.9, mar=c(0,4,5.1,2), xlim=c(-.5,.5))
dev.off()
}
worldcup_plot(fit_noprior, "worldcup1_noprior.png")
I put in the xlim values in that last line to make the graph look nice, after seeing the first version of the plot. And I also played around a bit with the margins (the argument "mar" to coefplot above) to get everything to look good. Overall, though, coefplot() worked wonderfully, straight out of the box. Thanks, Yu-Sung!
Similar to before but much noisier.
Act 2: Checking the fit of model to data
OK, fine. Now let's check model fit. For this we'll go back to the model worldcup_matt.stan which includes the prior ranking as a linear predictor. For each match we can compute an expected outcome based on the model and a 95% predictive interval based on the t distribution. This is all on the signed sqrt scale so we can do a signed square to put it on the original scale, then compare to the actual game outcomes.
Here's the R code (which, as usual, took a few iterations to debug; I'm not showing all my steps here):
expected_on_sqrt_scale <- a_hat[team1] - a_hat[team2]
sigma_y_sims <- sims$sigma_y
interval_975 <- median(qt(.975,df)*sigma_y_sims)
signed_square <- function (a) {sign(a)*a^2}
lower <- signed_square(expected_on_sqrt_scale - interval_975)
upper <- signed_square(expected_on_sqrt_scale + interval_975)
png ("worldcup2.png", height=1000, width=500)
coefplot (rev(score1 - score2), sds=rep(0, ngames),
lower.conf.bounds=rev(lower), upper.conf.bounds=rev(upper),
varnames=rev(paste(teams[team1], "vs.", teams[team2])),
main="Game score differentials\ncompared to 95% predictive interval from model\n",
mar=c(0,7,6,2))
dev.off ()
In the code above, I gave the graph a height of 1000 to allow room for all the games, and a width of 500 to conveniently fit on the blog page. Also I went to the trouble to explicitly state in the title that the intervals were 95%.
And here's what we get:
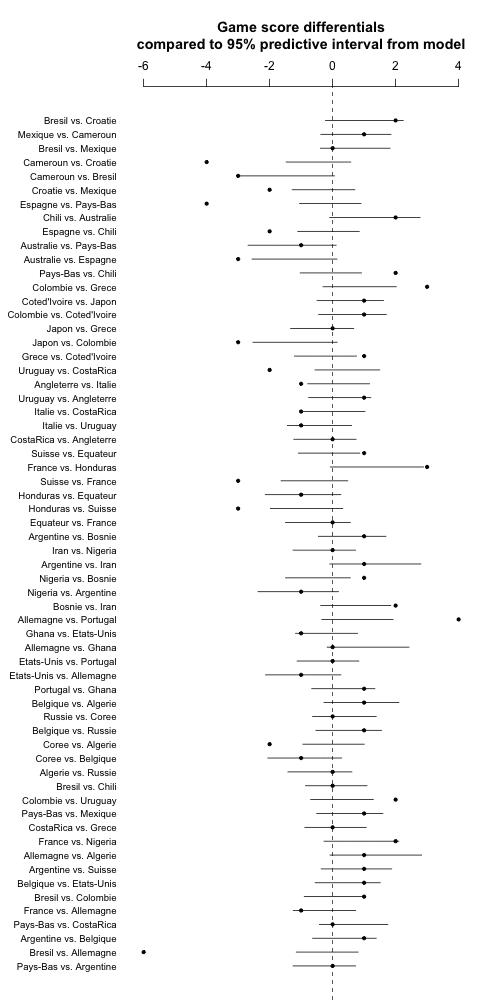
Whoa! Some majorly bad fit here. Even forgetting about Brazil vs. Germany, lots more than 5% of the points are outside the 95% intervals. My first thought was to play with the t degrees of freedom, but that can't really be the solution. And indeed switching to a t_4, or going the next step and estimating the degrees of freedom from the data (using the gamma(2,0.1) prior restricted to df>1, as recommended by Aki) didn't do much either.
Act 3: Thinking hard about the model. What to do next?
So then I got to thinking about problems with the model. Square root or no square root, the model is only approximate, indeed it's not a generative model at all, as it makes continuous predictions for discrete data. So my next step was to take the probabilities from my model, use them as predictions for each discrete score differential outcome (-6, -5, -4, . . ., up to +6) and then use these probabilities for a multinomial likelihood.
I won't copy the model in this post but it's included in the zipfile that I've attached here. The model didn't work at all and I didn't get around to fixing it.
Indeed, once we move to directly modeling the discrete data, a latent-data approach seems like it might be more reasonable, perhaps something a simple as an ordered logit or maybe something more tailored to the particular application.
Ordered logit's in the Stan manual so it shouldn't be too difficult to implement. But at this point I was going to bed and I knew I wouldn't have time to debug the model the next day (that is, today) so I resolved to just write up what I did do and be open about the difficulties.
These difficulties are not, fundamentally, R or Stan problems. Rather, they represent the challenges that arise when analyzing any new problem statistically.
Act 4: Rethinking the predictive intervals
But then, while typing up the above (it's taken me about an hour), I realized that my predictive intervals were too narrow because they're based on point estimates of the team abilities. How could I have been so foolish??
Now I'm excited. (And I'm writing here in real time, i.e. I have not yet cleaned up my code and recomputed those predictive error bounds.) Maybe everything will work out. That would make me so happy! The fractal nature of scientific revolutions, indeed.
OK, let's go to it.
*Pause while I code*
OK, that wan't too bad. First I refit the model using a zillion iterations so I can get the predictive intervals using simulation without worrying about anything:
fit <- stan_run("worldcup_matt.stan", data=data, chains=4, iter=5000)
print(fit)
Now the code:
sims <- extract (fit)
a_sims <- sims$a
sigma_y_sims <- sims$sigma_y
nsims <- length(sigma_y_sims)
random_outcome <- array(NA, c(nsims,ngames))
for (s in 1:nsims){
random_outcome_on_sqrt_scale <- (a_sims[s,team1] - a_sims[s,team2]) + rt(ngames,df)*sigma_y_sims[s]
random_outcome[s,] <- signed_square(random_outcome_on_sqrt_scale)
}
sim_quantiles <- array(NA,c(ngames,2))
for (i in 1:ngames){
sim_quantiles[i,] <- quantile(random_outcome[,i], c(.025,.975))
}
png ("worldcup3.png", height=1000, width=500)
coefplot (rev(score1 - score2), sds=rep(0, ngames),
lower.conf.bounds=rev(sim_quantiles[,1]), upper.conf.bounds=rev(sim_quantiles[,2]),
varnames=rev(paste(teams[team1], "vs.", teams[team2])),
main="Game score differentials\ncompared to 95% predictive interval from model\n",
mar=c(0,7,6,2))
dev.off ()
And now . . . the graph:
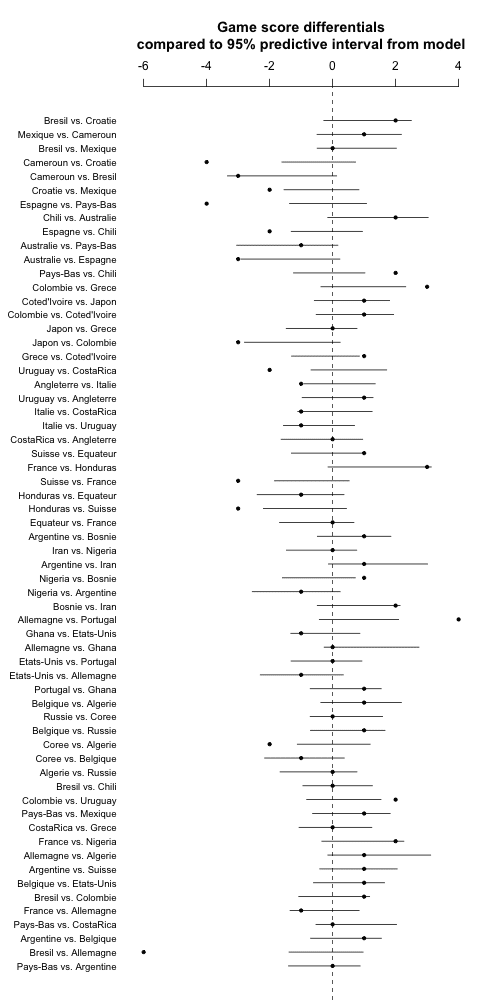
Hmm, the uncertainty bars are barely wider than before. So time for a brief re-think. The problem is that the predictions are continuous and the data are discrete. The easiest reasonable way to get discrete predictions from the model is to simply round to the nearest integer. So we'll do this, just changing the appropriate line in the above code to:
sim_quantiles[i,] <- quantile(round(random_outcome[,i]), c(.025,.975))
Aaaaand, here's the new graph:
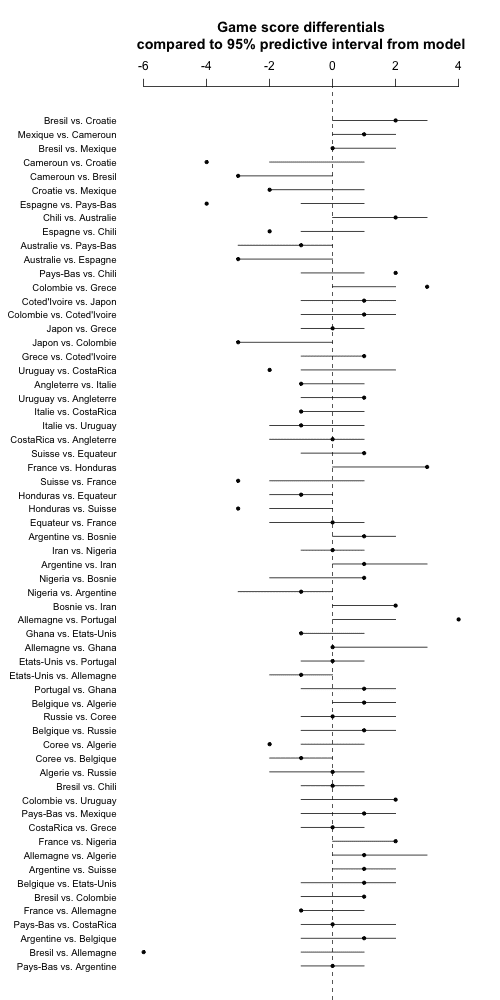
Still no good. Many more than 1/20 of the points are outside the 95% predictive intervals.
This is particularly bad given that the model was fit to the data and the above predictions are not cross-validated, hence we'd actually expect a bit of overcoverage.
One last thing: Instead of plotting the games in order of the data, I'll order them by expected score differential. I'll do it using difference in prior ranks so as not to poison the well with the estimates based on the data. Also I'll go back to the continuous predictive intervals as they show a bit more information:
a_hat <- colMeans(a_sims)
new_order <- order(a_hat[team1] - a_hat[team2])
for (i in 1:ngames){
sim_quantiles[i,] <- quantile(random_outcome[,i], c(.025,.975))
}
png ("worldcup5.png", height=1000, width=500)
coefplot ((score1 - score2)[new_order], sds=rep(0, ngames),
lower.conf.bounds=sim_quantiles[new_order,1], upper.conf.bounds=sim_quantiles[new_order,2],
varnames=paste(teams[team1[new_order]], "vs.", teams[team2[new_order]]),
main="Game score differentials\ncompared to 95% predictive interval from model\n",
mar=c(0,7,6,2))
dev.off ()
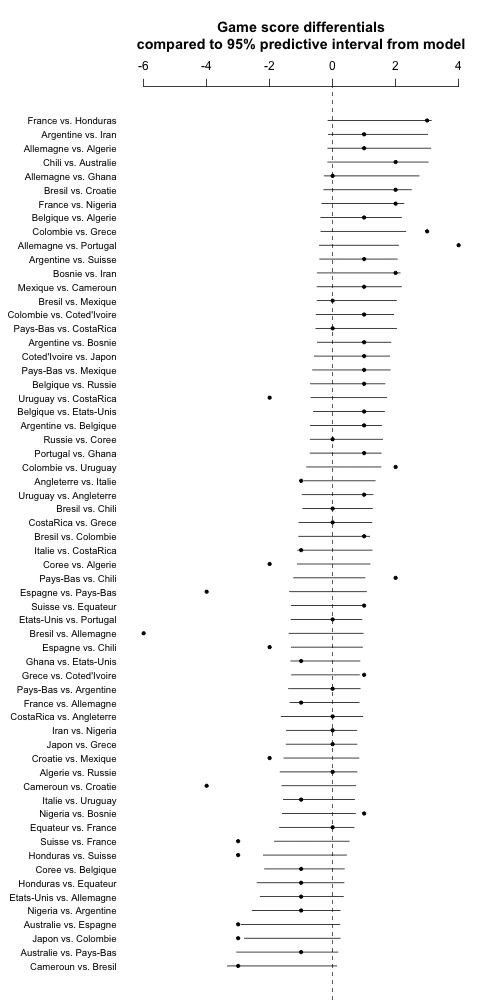
Hey, this worked on the first try! Cool.
But now I'm realizing one more thing. Each game has an official home and away team but this direction is pretty much arbitrary. So I'm going to flip each game so it's favorite vs. underdog, with favorite and underdog determined by the prior ranking.
So here it is, with results listed in order from expected blowouts to expected close matches:
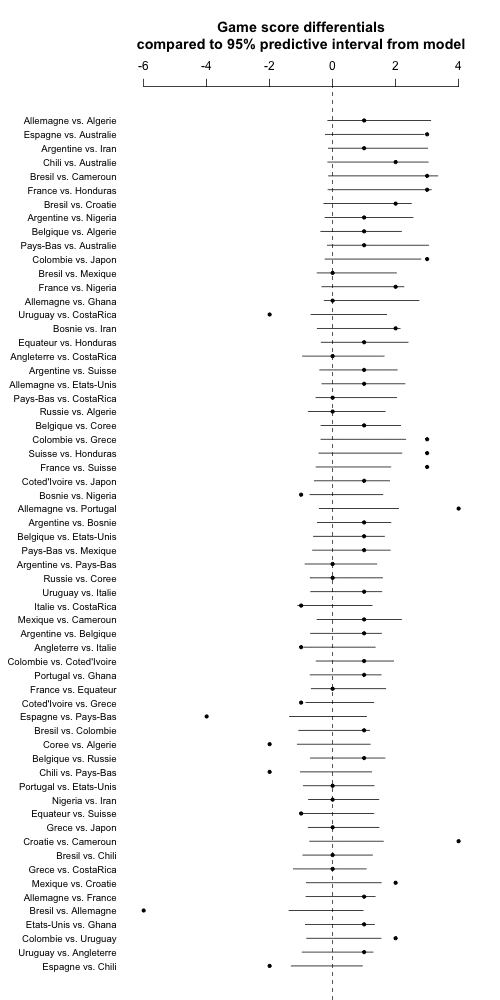
Again, lots of outliers, indicating that my model sucks. Maybe there's also some weird thing going on with Jacobians when I'm doing the square root transformations. Really I think the thing to do is to build a discrete-data model. In 2018, perhaps.
Again, all the data and code are here. (I did not include last night's Holland/Brazil game but of course it would be trivial to update the analyses if you want.)
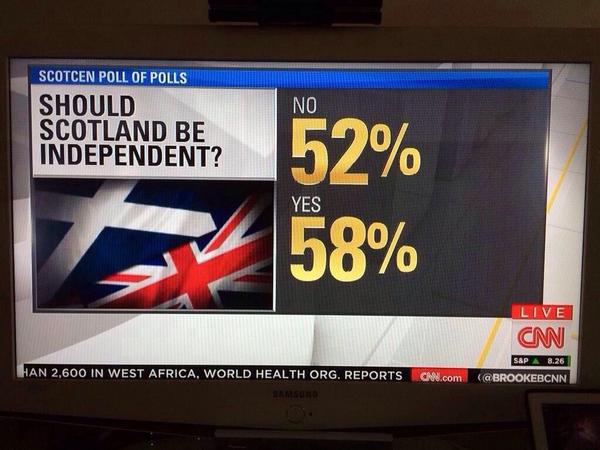
P.S. In the 9 June post linked above, Nate wrote that his method estimates that "a 20 percent chance that both the Netherlands and Chile play up to the higher end of the range, or they get a lucky bounce, or Australia pulls off a miracle, and Spain fails to advance despite wholly deserving to." I can't fault the estimate---after all, 1-in-5 events happen all the time---but I can't see why he was so sure that if Spain loses, that they still wholly deserved to win. They lost 5-1 to Holland and 2-0 to Chile so it doesn't seem like just a lucky bounce. At some point you have to say that if you lost, you got what you deserved, no?
P.P.S. The text in those png graphs is pretty hard to read. Would jpg be better? I'd rather not use pdf because then I'd need to convert it into an image file before uploading it onto the blog post.
P.P.P.S. I found a bug! The story is here.
 Here’s some things that have been going on with Stan since the last week’s roundup
Here’s some things that have been going on with Stan since the last week’s roundup