Economist Gary Smith sends along this post with the above title and the subtitle, “Market prices are not invariably equal to intrinsic values.” Here’s Smith:
For a while, there was a popular belief among finance professors that the stock market is “efficient” in the sense that stock prices are always correct — the prices that an all-knowing God would set. Thus, investors can buy any stock, even a randomly selected stock, and be confident that they are paying a fair price.
This belief was based on seemingly overwhelming evidence that changes in stock prices are difficult to predict. Efficient market enthusiasts argued that if stock prices are always correct, taking into account all currently available information, then any changes in stock prices must be due to new information which, by definition, is impossible to predict. Therefore, the evidence that changes in stock prices are hard to predict proves that the stock market is efficient.
This argument is a common fallacy. The fact that A implies B does not mean that B implies A. . . Here, the fact that an efficient stock market implies that stock prices are impossible to predict does not mean that if stock prices are impossible to predict then the stock market must be efficient. . . .
For example, the crazy gyrations in bitcoin prices are ample evidence that financial markets are not efficient. Since bitcoins generate no income, their intrinsic value is zero, yet people have paid hundreds, thousands, and tens of thousands of dollars for bitcoins. One explanation is that the evidence is strong that bitcoin prices have been manipulated by pump-and-dump schemes in which the unscrupulous circulate boisterous rumors while they trade bitcoin back and forth among themselves at higher and higher prices, and then sell to the naive who are lured into the market by the rumors and seemingly ever-rising prices.
One fascinating test of the pump-and-dump theory is based on a remarkable relationship known as Benford’s law. . . .
We’ve talked about Benford’s law before—it’s even in Teaching Statistics: A Bag of Tricks—so I’ll skip a few paragraphs of Smith’s exposition and get to the part that’s new to me:
For example, if we compare the price of a company’s stock one day and the price several days later, the price several days later is determined by the product of the daily percentage changes and, so, is governed by Benford’s law. To test this, I [Smith] looked at the prices of all stocks traded on the New York Stock Exchange (NYSE) on July 6, 2021. For 29.1 percent of the stocks, the leading digit was 1, which is close to the 30.1 percent implied by Benford’s law. The number 9 was the leading digit for only 4.8 percent of the stocks, which is close to the 4.6 percent implied by Benford’s Law. Figure 1 shows the full theoretical and empirical distributions. The close correspondence is striking for such a relatively small data set.
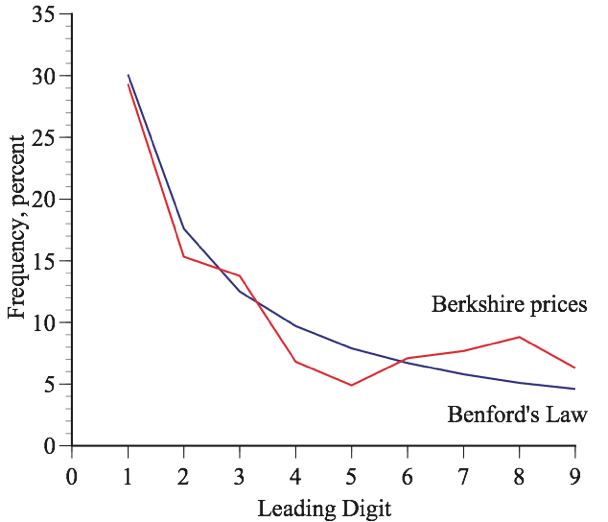
Figure 2 compares the distribution of the leading digits of the price of Berkshire Hathaway stock since 1980. Again, the fit is not perfect but reasonably close.
Benford’s law is more than just a surprising relationship; it can also be used to detect fraud. When people make up data, it is tempting to assume that, to avoid detection, the numbers should “look” random with every digit showing up equally often and no suspicious patterns, like five 1s in a row. However, if it is a situation where Benford’s law holds, there should be more 1s than 2s, more 2s than 3s, and so on.
Since a company’s revenue, costs, profits, and other measures of financial performance are likely to grow over time by percentages, they should be governed by Benford’s law. Thus, Benford’s law can and has been used to identify accounting fraud.
It can also be used to detect fraudulent bitcoin trades — so-called wash sales where a group of conspirators trade bitcoin back and forth among themselves at ever higher prices. Since increases in bitcoin prices are likely to be multiplicative, they should be governed by Benford’s law. They are not. Figure 3 shows the distribution of the leading digits of daily bitcoin prices back to 2014. Small digits appeared somewhat more often than large digits, but not nearly as often as implied by Benford’s law.
I saw this and I was like, well, yeah, isn’t all bitcoin use either crime or manipulation?
But then I realized, no, that’s not all of it. Some bitcoin playas are motivated by politics, some by fomo, some are doing anti-virtue signaling (it’s the investment equivalent of rolling coal), and others are just gambling for fun. There’s a lot going on, and people have lots of reasons for doing things.
P.S. Some questions were raised in comments. If you’re further interested in the topic, you could read the paper by Cong et al. linked above.


What the? First of all, the fit to benfords law only looks slightly worse than the Berkshire graph. Second, what is his theory about why the coin prices wouldn’t follow Benfords law? The typical theory is that people are choosing the fake numbers, but that’s obviously not possible with Bitcoin (unless the schemers were making 100% of the trades. This seems like a silly argument.
1. I think the fit is actually much worse than Berkshire on the left side of the graph
2. I agree that the argument here is weak. Multiplicative/logarithmic growth isn’t enough to guarantee Benford’s law. The growth needs to push the numbers to be spread out thinly over a couple orders of magnitude. So weak multiplicative growth over a short time scale won’t show the behavior for some base of representation. That doesn’t really apply to bitcoin, I’m just being pedantic. The bigger problem is that this is the same family of argument as the whole election fraud thing. We kind of expect bitcoin to look like a financial security, but it doesn’t, =/> bitcoin is fraudulent. All he’s shown is that bitcoin is unusual, that’s far from a smoking gun and doesn’t really suggest his vague interpretation. Anomalous observations just invite more analysis.
One possible story is that the pumpers pump until just before they reach some cutoff order of magnitude, then dump. For example, if they tended to start dumping when prices reach 9,000, just before crossing over to 10,000.
For the record, I do think pump and dumps are disconcertingly powerful in cryptocurrency trading, and function as a counterexample to strong efficient market hypotheses.
In fact, I’d argue that these
give a non-fraud explanation for why Benford’s law wouldn’t apply to bitcoin. Bitcoin is driven by either speculation or a shift to bitcoin as currency (hah!), and is definitively not driven by revenue, costs, profits, or any of those things that demonstrate multiplicative growth.
An inflation hedge IS a multiplier. With a fixed supply of btc and a perpetually increasing supply of fiat, the ratio will multiply the compared price to btc long term. Also,if the internet age has taught us nothing else, the immense power of the network effect is foundational to future growth. And unlike networks like myspace or yahoo, this network doesn’t depend on a ceo and a handful of project managers to guess at profitable decisions to keep themselves afloat. No one has to worry that btc will go out of business or need a government bailout like the banks.The network will live on in the security of it’s design.
And the Berkshire Hathaway check goes back to the eighties. Starting also in 2014 the leading digits are 1, 2, 3 and 4. Only 1 and 2 if we look at the class B shares.
Much worse.
And over a long period/many trials.
I know little about Bitcoin, so I guess it’s possible. I personally have a low prior that such the price is easily controllable at such a scale. Either way, it feels like he’s committing the same fallacy he was complaining about. “If Bitcoin is fraudulent, it won’t follow Benford’s Law. It doesn’t follow Benford’s Law, therefore Bitcoin’s fraudulent.”
I feel like there could be alternative hypotheses, like Benford’s Law only applying on a longer time horizon, or Bitcoin being a boom-and-bust asset, where people tend to pull back when the price nears adding a new digit (reducing frequencies on ones). Who knows.
I had to go back and follow the link to ensure it wasn’t some parody of all the nonsense back in November of Benford’s Law “proving” election fraud.
Given how often it’s misapplied, my policy going forward will be to always doubt fraud accusations based on Benford’s Law.
What a terrible analysis!
1 Looking at the statistics of digits only makes sense if one has a large ensemble of values. Suppose one has only one item, like the bitcoin price, over a fairly small interval of time, like a few years. Does one really expect an “ergodic” sampling of digits? For the entire span of 2015 and 2016, if I read this correctly, the price was between 200 and 900 — i.e. no “1”s sampled as leading digits. Similarly from about April 2018 to June 2019, the price was in the >= $2k and <= 9k range, possibly a sign of nefarious avoidance of the number "1" , or possibly a sign that the price was between $2 and $9k.
2 If I flip a coin 10 times, I shouldn't be surprised to get 6 heads. If I flip a coin 10,000,000 times, I *should* be surprised to get 6,000,000 heads. For a given number of coin flips, I should be able to state the uncertainty in my prediction for numbers of heads. The author should be able to state the uncertainty in the expected range of "Benford's law" predictions. Is Bitcoin (or Berkshire) inside or outside that?
3 As mentioned in a comment above, how exactly would this manipulation occur?
4 Even if (doubtful as it is) the expectation of Benford's law is reasonable and the data don't follow it, this doesn't imply that active manipulation drives that. As the author notes, but doesn't apply, "The fact that A implies B does not mean that B implies A."
I do like the idea of looking at the statistics of these things, though.
“how exactly would this manipulation occur?”
zakly!
What’s the formula for market manipulation that the evil geniuses have figured out but which no one else knows? If it’s so powerful, why stick to bitcoin? Why not Li, Au, soy beans and pea gravel?
Anon:
You don’t have to be evil or a genius to manipulate a market. You have to be in the right place in the right time and find a rich enough seam of suckers.
Puffing an investment that’s already a social phenomenon is a far cry from manipulating a single commodity or financial instrument for years on end.
I have no opinion about the analysis, but bitcoin trading bears almost no resemblance to that of mature markets like those for commodities, stocks, or bonds. Bitcoin and other cryptos are thinly traded and have extremely high transaction costs and barriers to entry. It is common for the prices to be significantly different on different exchanges, something that shouldn’t happen in a mature market. The exchanges are notorious for getting hacked or “rug-pulled” or going down mysteriously right when there’s a major price movement. And there is no regulation to prevent wash sales, insider trading, or bucketeering.
Wash trading (self-trading to manipulate prices and fake volume)
Painting the tape (faking volume, suckering technical traders, pump and dump)
Spoofing (faking demand, price manipulation on counter trades)
these are banned and generally criminal in equity and commodity markets
“how exactly would this manipulation occur?”
1. Create a stablecoin, let’s call it TUSD.
2. Use dollars to mint TUSD, use those to buy bitcoins.
3. Back newly printed TUSD with holdings in bitcoin.
4. Use those fresh TUSD to buy more bitcoin.
Rinse and repeat
Yes, the fact that bitcoin prices don’t conform to Benford’s law doesn’t prove market manipulation (and the fact that a company’s balance sheet doesn’t follow Benford’s law doesn’t prove fraud), but it makes one wonder.
The market-manipulation hypothesis is not far-fetched. In 2019 the Wall Street Journal reported that nearly 95 percent of the reported trading in bitcoin are fake trades intended to manipulate prices. A 2020 study published in the Journal of Finance concluded that nearly all of the rise in bitcoin prices in 2017 was due to trading by one large, unidentified trader using another digital currency, called Tether, to buy bitcoin. In a 2021 report, Research Affiliates, a widely respected investment management company, concluded that,
perhaps BTC is just a bubble driven by a frenzy of retail, and some institutional, money eager to get a piece of the action. Alternatively, and far likelier in my opinion, is that this “bubble” is more fraud than frenzy.
If market manipulators trade among themselves to keep the price within a certain range or trade back-and-forth among themselves at linearly high prices ($100, $150, $200, …), Benford’s law may be violated.
Starting on September 17, 2014, with an initial price of $457,33, there have been 2,488 daily bitcoin prices. The daily percentage return over this period had a mean of 0.25 and a standard deviation of 3.93. Compared to the actual distribution of leading digits, the hypothetical distribution of leading digits if each day’s percentage return had been drawn from a Normal distribution with a mean of 0.25 and a standard deviation of 3.93 fits Benford’s law closely. (I don’t seem to be able to attach a figure here, but I will send privately if you are interested.) The shape is little affected by serial correlation in the returns. It would be affected by the kind of market manipulation described above.
“the hypothetical distribution of leading digits if each day’s percentage return had been drawn from a Normal distribution with a mean of 0.25 and a standard deviation of 3.93 fits Benford’s law closely.”
Are you sure? Quickly doing this myself, and running it repeatedly, sometimes it looks Benford-like, sometimes wildly different. You may want to check this.
MATLAB code:
N = 2488; % number of days, after start
x = zeros(N+1,1);
x(1) = 457.33; % starting value
mean_r = 0.25; % mean percentage increase
std_r = 3.93; % standard dev. of percentage increase
r = mean_r + std_r*randn(N, 1); % Gaussian-distributed random increases
for j=2:(N+1)
x(j) = x(j-1)*(1+r(j-1)/100);
end
figure; plot(x)
firstDigit = floor(x./(10.^floor(log10(x)))); % the first digit of each number
figure; plot(firstDigit)
figure; histogram(firstDigit)
Hi Raghu,
I did 100,000 simulations and tabulated the average in order to estimate the probability distribution.
Thanks for replying!
The ensemble average of 100,000 2,488-day simulations will certainly follow Benford’s law; this doesn’t tell us whether we should expect a *single* 2,488 run to nicely follow Benford’s law. Again, it’s like saying that because as N -> infinity coin flips are 50% heads, we should consider 6-heads in 10-flips as evidence of an unfair coin.
Yep, that’s what statistical tests are for. It’s more work than I want to do, but I am pretty confident that a comparison of the empirical bitcoin distribution and the probabilistic Benford distribution has a low p-value.
More generally, the mathematical derivations of Benford’s law are derivations of theoretical probability distributions; for example,
Boyle, J. 1994. An application of Fourier series to the most significant digit problem. American Mathematical Monthly. 101(9):879-886.
I was a bit dismissive earlier, sorry about that.
I really appreciate the analysis you’ve been doing and for expanding on your reasoning here, Gary. This is an important problem, since crypto remains inundated with scams. A lot of people fall prey to ponzi schemes or exchanges that fake trades to look popular and then steal money from users. Identifying manipulations is a valuable public service.
As I don’t really look into fraud, I’d like to pick your brain on a couple points:
1) Do manipulators often work on linear scales instead of multiplicative? I’d have assumed they’d want x% return on investment.
2) How many people are legitimately trading Bitcoin? How easy is it for a subgroup with a relatively small fraction of the total dollar volume to manipulate the price? Is it mostly done through changing the expectations of others?
No worries.
1. Who knows what goes on in evil minds, but it seemed possible that a person who wants to pump up a price might think that a linear climb appears to be “natural.” The objective is not generate returns directly from the wash trades but to lure in suckers who will buy bitcoin at artificially high prices. Wash trades to support a price and keep suckers from fleeing would also generate non-Bedford prices.
2. As per my earlier reply:
In 2019 the Wall Street Journal reported that nearly 95 percent of the reported trading in bitcoin are fake trades intended to manipulate prices. A 2020 study published in the Journal of Finance concluded that nearly all of the rise in bitcoin prices in 2017 was due to trading by one large, unidentified trader using another digital currency, called Tether, to buy bitcoin. In a 2021 report, Research Affiliates, a widely respected investment management company, concluded that,
perhaps BTC is just a bubble driven by a frenzy of retail, and some institutional, money eager to get a piece of the action. Alternatively, and far likelier in my opinion, is that this “bubble” is more fraud than frenzy.
Proposition: every time one reads an analysis invoking Benford’s Law, one’s confidence in real-life applicability of Benford’s Law decreases.
This story today:
https://www.cnbc.com/2021/07/14/dogecoin-co-creator-jackson-palmer-criticizes-the-crypto-industry.html
This analysis makes no sense, particularly when traders can get trades filled at limit prices, which is not at all evidence of fraud, but the fundamental misunderstanding is on market efficiency. I know of no one who believes, or ever believed, that any security prices are the prices “an all-knowing God would set,” at least without some notion of what objective function our all-knowing God is using, which no one has. The unpredictability of prices is in fact the Strong Law of Market Efficiency, which you might guess by its name is far too strong to be observed in practice — lots of prices have various degrees of predictability which even, on occasion, exceed the transaction costs of trying to profit from that predictability. The Strong Law simply implies that all knowledge, private and public, is impounded into the price *including private information about price manipulation.*
A few true believers:
Chicago professor and Nobel Laureate Eugene Fama described
“an ‘efficient’ market for securities, that is, a market where, given the available information, actual prices at every point in time represent very good estimates of intrinsic values.”
Michael C. Jensen, professor emeritus, Harvard Business School, past President of the American Finance Association:
“The vast scientific evidence on the theory of efficient markets indicates that, in the absence of inside information, a security’s market price represents the best available estimate of its true value.”
A simple question: Do you think bitcoin prices are equal to intrinsic values?
Here, you illustrate a common misunderstanding of the “efficient market hypothesis.” One that Gary Smith wants to promulgate, perhaps.
The notion is that markets prices adjust quickly in response to new information. It is NOT that they have some kind of magical access to information about the future. Both your quotes above reflect that.
There is no question that this characterizes essentially all of the most important markets, and applies in a wide range of scales, from your local farmer’s market to the NYSE to FCOJ futures.
I think that saying that “there is no question” may be a bit too strong. Or maybe that “essentially” has to be understood in a quite broad sense.
https://eml.berkeley.edu/~craine/EconH195/Fall_15/webpage/Shiller_Efficient%20Mkts.pdf
My main point is a claim of market efficiency is not a claim for wisdom, rationality, or optimality under any metric. Especially, it is not a claim for a “rational actor model.” (Although “rational actor model + noise” is often useful model, if not a true one.) The Dutch tulip bulb market in the 17th century was not notably inefficient, for all it’s strangeness.
I’d understand Shiller as unearthing a new source of information, for the market to (efficiently) incorporate. If not, why ain’t you rich?
Dzhaughn:
I can’t speak for Carlos, but some of the people who comment on this blog are, in fact, rich. Rich people want to talk about statistics too!
Shiller agrees that changes in stock prices are difficult to predict (so it is hard to get rich predicting changes in stock prices). The disagreement is about the reason changes in stock prices are difficult to predict.
Some say it is because stock prices are invariably close to intrinsic values, taking into account all available information. Since new information that will change intrinsic values and stock prices is, by definition, impossible to predict (otherwise, it wouldn’t be new information), changes in stock prices are impossible predict.
Others say that stock prices are buffeted by fads and follies (what Keynes called “animal spirits”) which can take prices far from intrinsic values but, nonetheless, are impossible to predict. As Keynes said, “Markets can remain irrational longer than you can remain solvent.”
> If not, why ain’t you rich?
Do you think that poker is purely a game of chance without any element of skill to it? If not, why didn’t you get rich playing poker. (If you did get rich playing poker, change “poker” to “golf” or whatever.)
Shiller’s response to the Fama/Jensen argument that the difficulty in predicting changes in stocks prices implies that stock prices are good estimates of intrinsic value (discounted value of anticipated cash flow):
“One form of this argument claims that . . . the real price of stocks is close to the intrinsic value, that is, the present value with constant discount rate of optimally forecasted future real dividends. This argument for the efficient markets hypothesis represents one of the most remarkable errors in the history of economic thought.”
Bitcoin is but one of many examples of prices that are not plausibly related to intrinsic values. Other examples are in my investments books and op-ed columns
What do you mean by “intrinsic values” or “true values” or, more precisely, what is it you think Fama and Jensen mean by those terms in their quotes?
When you define what you mean (or what you think Fama and Jensen mean), I’ll be happy to answer your question about bitcoin.
Projected future dividends or other cashflows, discounted relative to a risk-free asset?
Bitcoin has no dividends or cashflows, so by that definition its intrinsic value is 0… the same as a $100 bill.
Hey—that’s 100 times the intrinsic value of a $1 bill!
Correct, that’s why Smith says above that its intrinsic value is zero. Of course, this argument presumes that we’re measuring value in terms of traditional currency as our numeraire. If you’re thinking about bitcoin as an investment or hoping to get rich off of it, you’re implicitly making that assumption.
If you’re a true believer, you expect to be able to exchange bitcoin for goods and services, so this argument is unconvincing, but if you’re reality-based bitcoin’s core technology is too hopelessly broken to be used in that way.
Somebody:
I’ve always assumed that Bitcoin, like Uber, is making a bet that it will at some point get covered by the government in some way. With Uber, my impression was that the plan was to give out enough cheap rides that a base of users would feel dependent on it, which in turn would motivate the government to give it an indefinite subsidy. Similarly for Bitcoin—but, for better or worse, Bitcoin seems to have become more political than Uber ever was. Anyway, I think the underlying “technology” is social more than anything else: the idea was to become ubiquitous like Facebook and then be too big to fail. As long as the probability of this happening is far enough away from zero, there’s your value.
That’s an interesting idea — something like a USD backed bitcoin, with the fed moving bitcoins back and forth between addresses like they do with the gold vaults under NYC?. I don’t know anything about the bitcoin project’s maintainers, so I’ll avoid speculating on that, but I can’t imagine bitcoin actually becoming critical infrastructure. It has a theoretical maximum of something like 800,000 transactions per day, so at best 1% of Americans get to make one bitcoin purchase a day. If enough people get “invested” in bitcoin through exchanges like coinbase and then it crashes, they might feel the need to bail retail investors out though, and I guess that does provide a value now through backwards induction. Bailouts are cashflow.
somebody:
The May 8th edition of The Economist had a special report on just that: so-called “govcoins” (https://www.economist.com/weeklyedition/2021-05-08). Certainly more feasible than bitcoin, but I still haven’t had the pleasure of coming across a problem solved by blockchain that wasn’t caused by blockchain in the first place.
Gary:
What’s the “intrinsic value” of gold? Palladium? Platinum or copper? The value is a function of the cost to produce the commodity. If gold could be produced for $100/oz world wide, the price would fall rapidly.
The same is true of bitcoin: it’s price is dependent on the cost of production. If the cost of production fell rapidly, the price of bitcoin would also fall.
The market value is a function of both supply (which subsumes cost) and demand. Something can be arbitrarily hard to produce and worth zero if nobody wants it. Something can be easy to produce and go up in price when all of a sudden everybody wants it.
The question is why do people want bitcoin? People want copper, platinum, and palladium because of their industrial applications. Wires, contact plating, etc. People want gold because people have always wanted gold for ten thousand years, so it’s reasonable to believe people will still want gold fifty years from now, making it a reasonable hedge against inflation or regime collapse. People might think people will still want bitcoins fifty years from now, but the evidence there is much shakier than for gold. First of all, gold has at least proved that it CAN function as a currency, while bitcoin provably cannot function as a currency.
Thanks to the dynamic mining difficulty, you have this backwards. The cost to produce bitcoin will adjust until it matches the market value.
“…stock prices are always correct — the prices that an all-knowing God would set.”
“Therefore, the evidence that changes in stock prices are hard to predict *proves* that the stock market is efficient.” (My emphasis added.)
This does not pass the Ideological Turing Test. I cannot tell if it is because the author is ignorant (doubtful given the credentials of the author) or because the author is unwilling to “steel man” a position he disagrees with (more likely given it’s 2021). It’s a cute rhetorical trick to push an opposing viewpoint further than the opposition does (the God metaphor being particularly egregious), but it is not a source of high-quality discourse.
Hi Will,
The quotations you cite are intended to represent arguments made by efficient market enthusiasts who believe that stock prices are good estimates of intrinsic value (the discounted cash flow from an asset). I disagree strongly.
Gold has no intrinsic value. It has industrial uses but it’s value is mostly a function of the cost of production, which is also true for bitcoin. The value of both is a function of the cost of the equipment required to extract the commodity.
Data’s adherence to Benford’s law is often interpreted, in application, as a test of whether a data set has been generated “naturally.” That is, if a known process can be established to be naturally Benfordian, but data allegedly produced through that process is non-Benfordian, it’s evidence that some other process (or mixture of processes) generated the data. I find it interesting that this is equivalent to showing that a dataset contains excess algorithmic information (complexity): we ought to be able to predict the rate of 1’s, 2’s, etc. in leading digits, in which case we could design an algorithm strictly using Benford’s law to efficiently compress the data. If we cannot, it implies that the data are “distributed random with respect to the Benford process,” or Benford-complex.
I have no deeper point here, just saying that I find it fascinating. :)
One can “detect” price manipulation in many places using this method. The first stock going up 10000% in the last decade that came to my mind was Tesla. And it looks fishy! Even after un-adjusting for the split to use the actual trading prices.
https://imgur.com/a/ulqNZ91
Top stock gainer for the last decade is by far Netflix. I analyzed its historical prices adjusted for stock splits for the period of 2002 – 2021 (https://www.macrotrends.net/stocks/charts/NFLX/netflix/stock-price-history). Price range of the stock covers 3 orders of magnitude. I used a nice easy free online tool (https://ezcalc.me/benfords-law-calculator/) and got the result that looks a bit better than Tesla but still is not complying with Benford’s Law! Considering period of 2009 – 2021 doesn’t change the picture.
> if we compare the price of a company’s stock one day and the price several days later, the price several days later is determined by the product of the daily percentage changes and, so, is governed by Benford’s law.
Take the stock of a company like Pfizer. If we compare the price on July 1st 1999 with the price today (or any day in the last 22 years), is it governed by Benford’s law? It seems that the leading digit has been only 1, 2, 3 or 4.
> To test this, (…)
That is testing something else.
>Market prices are not invariably equal to intrinsic values.
Isn’t this well known since at least the work of Shiller?
I’m glad there are people investigating the market manipulation occurring in Bitcoin. Many people have lost money in these markets, unaware of the unregulated and frequently criminal nature of these markets.
In addition, the method introduced seems broadly applicable to discovering a wide range of fraud. In fact, I ran an analysis of Walmart over a five year time period. I found something intriguing. Walmart’s opening prices clearly deviate from Benford’s law. For example, Benford’s law predicts that we would see a leading 9 about 4.6% of the time. In fact, we see this 15.8% of the time.
Here is a graph. Blue is the theoretical distribution. Red is the actual distribution.
https://i.imgur.com/oqQmCFi.png
Quite damning, no?
Some may object that this may be the result of chance. I ran a chi-square test. Assuming that legitimate trading activity follows a probability distribution given by Benford’s law, the chance that this is legitimate activity is less than one in a quadrillion.
Here’s the output from R:
Pearson’s Chi-squared test
data: stock$Open
X-squared = 2868, df = 89, p-value < 2.2e-16
Njo:
I have no knowledge of Walmart, but, speaking generally, you’ll expect Benford-like behavior for a quantity that varies over several orders of magnitude, but not if it varies by only a small amount. Bitcoin has been all over the map, which is why a Benford analysis might be reasonable there, and the NYSE is a whole bunch of stocks. A single stock could have a price that varies by less than an order of magnitude, in which case there’d be no reason to expect a Benford-like distribution.
> A single stock could have a price that varies by less than an order of magnitude, in which case there’d be no reason to expect a Benford-like distribution.
Even if the price range of a stock covers more than an order of magnitude that is not a reason to expect a Benford-like distribution.
In the example of Tesla, it went from less than $20 to more than $2000 (over $4000 if it had not been split last year).
It doesn’t follow the Benford’s Law distribution but there was no reason to expect that in the first place.
My comment on the Walmart data is below; I forgot to hit the right “reply” link.
I’m kicking myself for spending five minutes on this, but anyway:
Downloading all the Walmart data, the non-Bedford-like appearance seems due to the last 13 years. In this period, the price is increases from about 50 to 150, for which it is *literally impossible* to have a starting digit of 2 or 3. The “null hypothesis” being a Bedford’s law distribution is clearly not applicable.
“Quite damning, no?”
No.
My first thought was, “Where is the positive control?” Are there examples of Benford’s law being used to detect fraud for a similar entity (speculative asset?) as Bitcoin?
Anon:
I think Bitcoin is the positive control here. But, as discussed in comments above, the Benford thing will only work if the price varies by some orders of magnitude.
How is it that the manipulation is supposed to happen in bitcoin? Whats the supposed mechanism for the violation of Benford’s law?
Richard:
See the above-linked paper by Cong et al.
This sophistry only got posted because it flattered Andrew’s “economists aren’t as smart as they think they are” instincts. It’s crap for all the reasons given in the other comments.
The truth about EMH is that economists study it a lot, it is “true” in broad strokes but false in its strongest claim, people can and do make money off of its falseness, but it is true enough that policy implications are basically the same as it were actually fully true. The main implication is that markets (of sufficient liquidity, etc.) usually offer a better forecast of various indicators than experts.
Rick:
You should take this one up directly with Gary Smith, as he’s the economist in this conversation.
“For a while, there was a popular belief among finance professors that the stock market is “efficient” in the sense that stock prices are always correct” – when I see statements like this I wonder what “correct” actually means. What is the unobserved truth to which a stock price refers, that can later be observed in order to check whether it was “correct” or not? It can’t really be a future stock price because that would just pass the problem on. But surely stock prices incorporate expectation about their future prices. They are correct in the trivial sense that they are what they are at any point, but how can they be correct or incorrect in any other sense?
Do a bootstrap analysis. Take the S&P500 and subsample 8 years for a given stock, calculate the line, and do this N times. Plot the resulting distribution. Does BTC’s line lie outside of the 95% confidence interval or not? My guess is no.
Why not include data from earlier than 2014? This API has data starting from 2010-07-17: https://api.coindesk.com/v1/bpi/historical/close.json?start=2010-07-17&end=2030-01-01
The paper talks about benfords law in relation to trading sizes, not the price.
We show that many unregulated crypto exchanges are engaged in excessive wash trading. Specifically, first-digit distributions of trade size follow Benford’s law for regulated exchanges, whereas nearly 30% of unregulated exchanges show violations.
Ben:
Thanks.
Their should be data from earlier than 2014, as Rune just mentioned we have data from 2010.
https://www.rasklån.no has charts dating back to 2010 also.