tl;dr. See point 4 below.
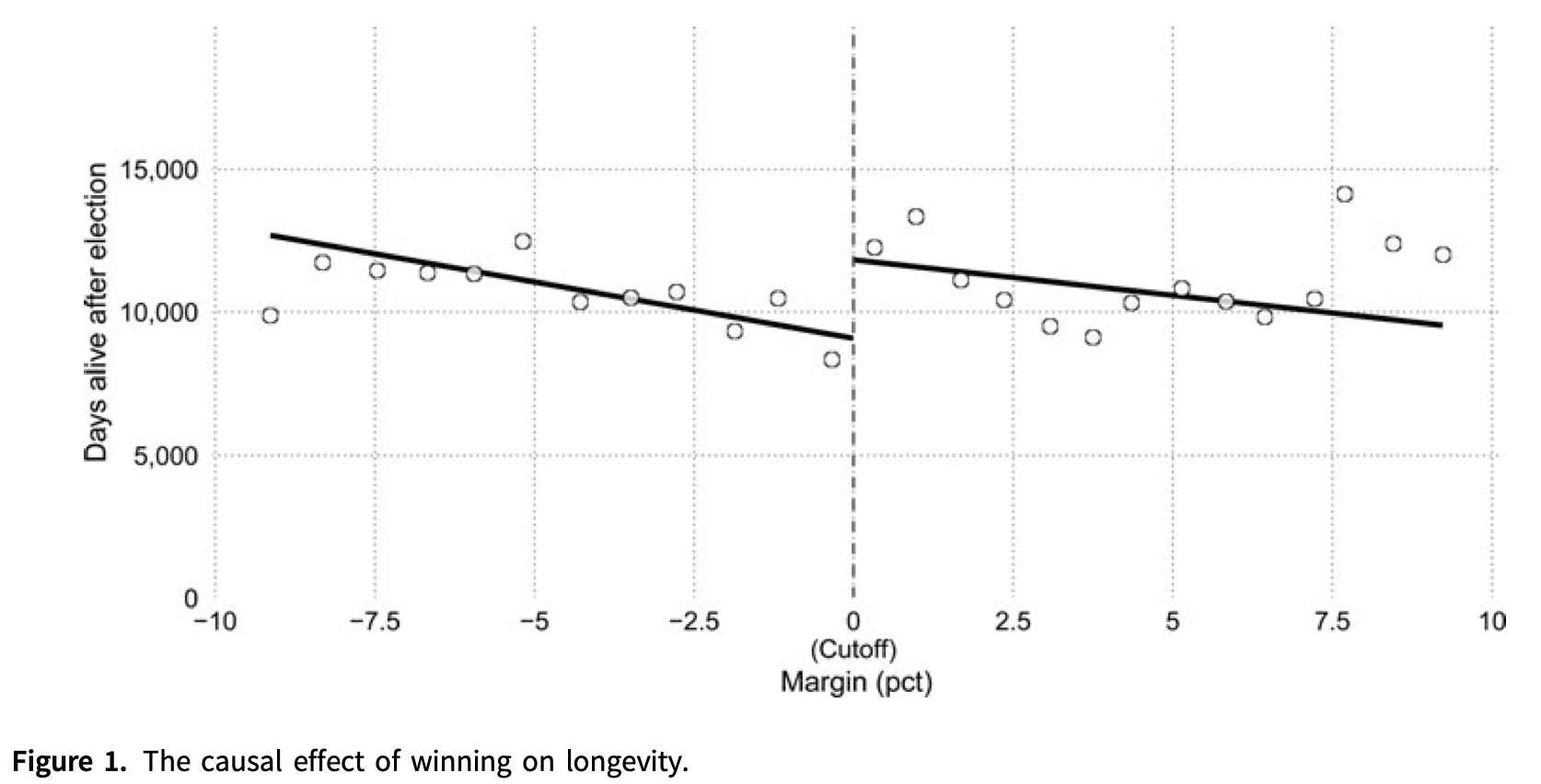
Despite the p-less-than-0.05 statistical significance of the discontinuity in the above graph, no, I do not believe that losing a close election causes U.S. governors to die 5-10 years longer, as was claimed in this recently published article.
Or, to put it another way: Despite the p-less-than-0.05 statistical significance of the discontinuity of the above graph, and despite the assurance of the authors that this finding is robust, no, I do not believe that winning a close election causes U.S. governors to live 5-10 years longer.
How can I say this? I will answer in five ways:
1. Common sense
2. Our experience as consumers of research
3. Statistical analysis
4. Statistical design
5. Sociology of science.
1. Common sense: 5-10 years is a huge amount of lifetime. Even if you imagine dramatic causal sequences (for example, you lose an election and become depressed and slide into alcoholism and then drive your car into a tree), it’s hard to imagine such a huge effect.
2. Our experience as consumers of research: The recent history of social and behavioral science is littered with published papers that made claims of implausibly large effects, supported by statistically significant comparisons and seemingly solid research methods, which did not hold up under replication or methodological scrutiny. Some familiar examples to readers of this blog include the claim that beautiful parents were 8 percentage points more likely to have girls, the claim that students at Cornell had extra-sensory perception, the claim that women were three times more likely to wear red or pink clothing during certain times of the month, the claim that single women were 20 percentage points more likely to support Barack Obama during certain times of the month, and the claim that political moderates perceived the shades of gray more accurately than extremists on the left and right. We’ve been burned before. We’ve been burned enough times that we realize we don’t have to follow Kahneman’s now-retired dictum that “you have no choice but to accept that the major conclusions of these studies are true.”
At this point, I recommend that you pause your reading now and go to this post, “50 shades of gray: A research story,” and read all of it. It won’t take long: it’s just two long paragraphs from an article of Nosek, Spies, and Motyl and then a few sentences of remarks from me.
OK, did you read “50 shades of gray: A research story”? Great. Now let’s continue.
3. Statistical analysis: If there truly is no such large effect that losing an election causing you to lose 5 to 10 years of life, then how could these researchers have found a comparison that was (a) statistically significant, and (b) robust to model perturbations? My quick answer is forking paths. I know some of you are gonna hate to hear it, but there it is. The above graph might look compelling, but here’s what the raw data look like:

For ease of interpretation I’ve plotted the data in years rather than days.
Now let’s throw a loess on there and see what we get:

And here are two loess fits, one for negative x and one for positive x:

Yup. Same old story. Fit a negative slope right near the discontinuity, and then a positive jump is needed to make everything work out. The point is not that loess is the right thing to do here; the point is that this is what’s in these data.
The fit is noisy, and finding the discontinuity all depends on there being this strong negative relation between future lifespan and vote margin in this one election—but just for vote margins in this +/- 5 percentage point range. Without that negative slope, the discontinuity goes away. It’s just like three examples discussed here.
At this point you might say, no, the authors actually fit a local linear regression, so we can’t blame the curve, and that their results were robust . . . OK, we’ll get to that. My first point here is that the data are super-noisy, and fitting different models to these data will give you much different results. Again, remember that it makes sense that the data are noisy—there’s no good reason to expect a strong relationship between vote margin in an election and the number of years that someone will live afterward. Indeed, from any usual way of looking at things, it’s ludicrous to think that a candidate’s life expectancy is:
30 years if he loses an election by 5 percentage points
25 years if he loses narrowly
35 years if he wins narrowly
30 years if he wins by 5 percentage points.
It’s a lot more believable that this variation is just noise, some artifact of the few hundred cases in this dataset, than that it represents some general truth about elections, or even about elections for governor.
And here’s a regression. I show a bunch of regressions (with code) at the end of the post; here’s one including all the elections between 1945 and 2012, excluding all missing data, and counting the first race for each candidate who ran for governor multiple times:
lm(formula = more_years ~ won + age + decades_since_1950 + margin,
data = data, subset = subset)
coef.est coef.se
(Intercept) 78.60 4.05
won 2.39 2.44
age -0.98 0.08
decades_since_1950 -0.21 0.51
margin -0.11 0.22
---
n = 311, k = 5
residual sd = 10.73, R-Squared = 0.35
The estimated effect is 2.4 years with a standard error of 2.4 years, i.e., consistent with noise.
But what about the robustness as reported in the published article? My answer to that is, first, the result is not so robust, as is indicated by the above graph and regression and demonstrated further in my P.S. below—and I wasn’t trying to make the result go away, I was just trying to replicate what they were doing in that paper,—and, second, let’s see what Uri Simonsohn had to say about this:
To demonstrate the problem I [Simonsohn] conducted exploratory analyses on the 2010 wave of the General Social Survey (GSS) until discovering an interesting correlation. If I were writing a paper about it, this is how I may motivate it:
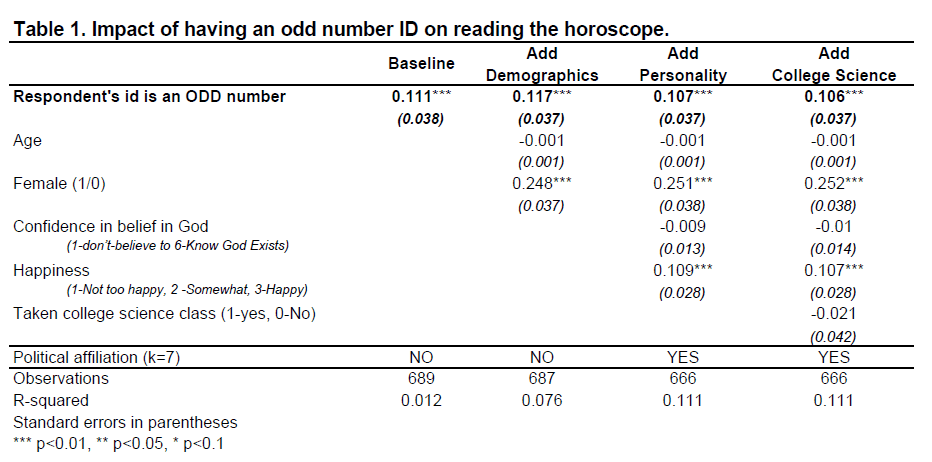
Based on the behavioral priming literature in psychology, which shows that activating one mental construct increases the tendency of people to engage in mentally related behaviors, one may conjecture that activating “oddness,” may lead people to act in less traditional ways, e.g., seeking information from non-traditional sources. I used data from the GSS and examined if respondents who were randomly assigned an odd respondent ID (1,3,5…) were more likely to report reading horoscopes.
The first column in the table below shows this implausible hypothesis was supported by the data, p<.01 (STATA code)
People are about 11 percentage points more likely to read the horoscope when they are randomly assigned an odd number by the GSS. Moreover, this estimate barely changes across alternative specifications that include more and more covariates, despite the notable increase in R2.
4. Statistical design: Another way to think about this is to consider the design of such a study. A priori we might consider an effect size of one additional year of life to be large, and on the border of plausibility. But this study has essentially no power to detect effects this small! You can see that from the standard errors on the regression. If an estimate of 5-10 years is two or three standard errors away from zero, than an effect of 1 year, or even 2 years, is statistically undetectable. So the study is really set up only to catch artifacts or noise. That’s the point of the “Power failure” paper by Button et al. (2012).
5. Sociology of science: If you are a social scientist, statistical methods should be your servant, not your master. It’s very tempting to say that the researchers who made the above graph followed the rules and that it’s not fair to pick on them. But the point of social science is not to follow the rules, it’s to gain understanding and make decisions. When following the rules gives silly results, it’s time to look more carefully at the rules and think hard about what went wrong. That’s what (many) psychologists did after the Bem ESP debacle and the rest of the replication crisis.
Yes, it’s possible that I’m wrong. Perhaps losing a close election really did kill these candidates for governor. It’s possible. But I don’t think so. I think this paper is just another example of statistical rule-following that’s out of control.
No smoking gun
It’s easy to criticize research when the forking paths are all out in the open (as with the ESP study) or when statistics show that your sample size is too low to detect anything by a factor of 100 (as in the beauty-and-sex-ratio example) or when there are obvious forking paths and a failed replication (as in the ovulation-and-clothing example) or when almost all the data have been excluded from the analysis (as in the union elections and stock price example) or when there’s flat-out research misconduct (as with pizzagate).
This example we’re discussing here is a bit different. It’s a clean analysis with clean data. The data are even publicly available (which allowed me to make the above graphs)! But, remember, honesty and transparency are not enough. If you do a study of an effect that is small and highly variable (which this one is: to the extent that winning or losing can have large effects on your lifespan, the effect will surely vary a lot from person to person), you’ve set yourself up for scientific failure: you’re working with noise.
I’m not happy about this, but that’s just how quantitative science works. So let me emphasize again that a study can be fatally flawed just by being underpowered, even if there’s no other obvious flaw in the study.
Or, to put it another way, there’s an attitude that causal identification + statistical significance = discovery, or that causal identification + robust statistical significance = discovery. But that attitude is mistaken. Even if you’re an honest and well-meaning researcher who has followed principles of open science.
P.S. R code is below. I followed the link at the published article and downloaded the data from here. The code didn’t quite run as is—the R code required a .csv file but all I could find was a .tab file, so I changed:
df_rdd <- fread("longevity.csv")
to
df_rdd <- fread("longevity.tab")
Then when I ran the next bit of the code:
if (sha1(df_rdd) != "300cc29bbecd2b630016c9bd2c8ef958dcc1b45d"){
error("Wrong data file loaded or data has been changed!") }
I got an error:
Error in error("Wrong data file loaded or data has been changed!") :
could not find function "error"
Sol I checked this:
sha1(df_rdd)
and got this:
"e26cc6acbed7a7144cd2886eb997d4ae262cf400"
So maybe the data did get changed! I have no idea. But I was able to reproduce the graphs so things were probably OK.
I also noticed some data problems, such as cases where the politician's death date came decades before his election. There were a bunch of these, for example see here:

I'm not trying to say that this is a horrible dataset. This is just what happens when you try to replicate someone's analyses. Problems come up.
Once I started to go through the data, I realized there are a lot of analysis choices. The article in question focuses on details of the discontinuity analysis, but that's really the least of it, considering that we have no real reason to think that the vote margin should be predictive of longevity. The most obvious thing is that the best predictor of how long you'll live in the future is . . . how long you've lived so far. So I included current age as a linear predictor in the model. It then would be natural to interact the win/loss indicator with age. That to me makes a lot more sense than interacting with the vote margin. In general, it makes sense to interact the treatment with the most important predictors in your data.
Another issue is what to do with candidates who are still living. The published analysis just discarded them. It would be more natural, I think, to include such data using survival analysis. I didn't do this, though, as it would take additional work. I guess that was the motivation of the authors, too. No shame in that---I cut corners with missing data all the time---but it is yet another researcher degree of freedom.
Another big concern is candidates who run in multiple elections. It's not appropriate to use a regression model assuming independent errors when you have the same outcome for many cases. To keep things simple, I just kept the first election in the dataset for each candidate, but of course that's not the only choice; instead you might, for example, use the average vote margin for all the elections where the candidate ran.
Finally, for the analysis itself: it seems that the published regressions were performed using an automatic regression discontinuity package, rdrobust. I'm sure this is fine for what it is, but, again, I think that in this observational study the vote margin is not the most important thing to adjust for. Sure, you want to adjust for it, as there's no overlap on this variable, but we simply don't have enough cases right near the margin (the zone where we might legitimately approximate win or loss as a randomly applied treatment) to rely on the RD. 400 or so cases is just not enough to estimate a realistic effect size here. To keep some control over the analyses, I just fit some simple regressions. It would be possible to include local bandwidths etc. if that were desired, but, again, that's not really the point. The discontinuity assignment is relevant to our analysis, but it's not the only thing going on, and we have to keep our eye on the big picture if we want to seriously estimate the treatment effect.
So now some code, which I ran after first running the script longevity.R that was included at the replication site. First I hacked the dates:
death_date <- sapply(df_rdd[,"death_date_imp"], as.character) living <- df_rdd[,"living"] == "yes" death_date[living] <- "2020-01-01" election_year <- as.vector(unlist(df_rdd[,"year"])) election_date <- paste(election_year, "-11-05", sep="") more_days <- as.vector(as.Date(death_date) - as.Date(election_date)) more_years <- more_days/365.24 age <- as.vector(unlist(df_rdd[,"living_day_imp_pre"]))/365.24
It turned out I didn't really need to do this, because the authors had made those date conversions, but I wanted to do it myself to make sure.
Next I cleaned the data, counting each candidate just once:
n <- nrow(df_rdd) name <- paste(unlist(df_rdd[,"cand_last"]), unlist(df_rdd[,"cand_first"]), unlist(df_rdd[,"cand_middle"])) first_race <- c(TRUE, name[2:n] != name[1:(n-1)]) margin <- as.vector(unlist(df_rdd[,"margin_pct_1"])) won <- ifelse(margin > 0, 1, 0) lifetime <- age + more_years decades_since_1950 <- (election_year - 1950)/10 data <- data.frame(margin, won, election_year, age, more_years, living, lifetime, decades_since_1950) subset <- first_race & election_year >= 1945 & election_year <= 2012 & abs(margin) < 10 & !living
Again, I know my code is ugly. I did check the results a bit, but I wouldn't be surprised if I introduced a few bugs. I created the decades_since_1950 variable as I had the idea that longevity might be increasing, and I put it in decades rather than years to get a more interpretable coefficient. I restricted the data to 1945-2012 and to candidates who were no longer alive at this time because that's what was done in the paper, and I considered election margins of less than 10 percentage points because that's what they showed in their graph, and also this did seem like a reasonable boundary for close elections that could've gone either way (so that we could consider it as a randomly assigned treatment).
Then some regressions. I first did them using stan_glm but just for convenience I'll give you straight lm code here, including the arm package to get the cleaner display:
library("arm")
fit_1a <- lm(more_years ~ won + age + decades_since_1950 + margin, data=data, subset=subset)
display(fit_1a)
fit_1b <- lm(more_years ~ won + age + won:age + decades_since_1950 + margin , data=data, subset=subset)
display(fit_1b)
The first model includes the most natural predictors; the second includes the interaction with age, as discussed above. And here are the results:
lm(formula = more_years ~ won + age + decades_since_1950 + margin,
data = data, subset = subset)
coef.est coef.se
(Intercept) 78.60 4.05
won 2.39 2.44
age -0.98 0.08
decades_since_1950 -0.21 0.51
margin -0.11 0.22
---
n = 311, k = 5
residual sd = 10.73, R-Squared = 0.35
lm(formula = more_years ~ won + age + won:age + decades_since_1950 +
margin, data = data, subset = subset)
coef.est coef.se
(Intercept) 78.81 5.41
won 1.92 8.25
age -0.98 0.10
decades_since_1950 -0.21 0.51
margin -0.11 0.22
won:age 0.01 0.16
---
n = 311, k = 6
residual sd = 10.75, R-Squared = 0.35
I was gonna start talking about how hard it would be to interpret the coefficient of the treatment ("won" = winning the election) in the second model, because of the interaction with age. But the coefficient for that interaction is so small and so noisy that let's just forget about it and go up to the earlier regression. The estimated treatment effect is 2.4 years (not 5-10 years) and its standard error is also 2.4.
What about excluding decades_since_1950?
lm(formula = more_years ~ won + age + margin, data = data, subset = subset)
coef.est coef.se
(Intercept) 78.62 4.05
won 2.36 2.44
age -0.99 0.08
margin -0.11 0.22
---
n = 311, k = 4
residual sd = 10.72, R-Squared = 0.35
Nahhh, it doesn't do much. We could exclude age also:
lm(formula = more_years ~ won + margin, data = data, subset = subset)
coef.est coef.se
(Intercept) 30.14 1.75
won 1.70 3.01
margin 0.10 0.27
---
n = 311, k = 3
residual sd = 13.25, R-Squared = 0.01
Now the estimate's even smaller and noisier! We should've kept age in the model in any case. We could up the power by including more elections:
subset2 <- first_race & election_year >= 1945 & election_year <= 2012 & abs(margin) < 20 & !living fit_1e <- lm(more_years ~ won + age + decades_since_1950 + margin, data=data, subset=subset2) display(fit_1e)
Which gives us:
lm(formula = more_years ~ won + age + decades_since_1950 + margin,
data = data, subset = subset2)
coef.est coef.se
(Intercept) 76.24 3.29
won 1.00 1.83
age -0.93 0.06
decades_since_1950 -0.18 0.39
margin 0.02 0.09
---
n = 497, k = 5
residual sd = 10.83, R-Squared = 0.33
Now we have almost 500 cases, but we're still not seeing that large and statistically significant effect.
Look. I'm not saying that my regressions are better than the ones in the published paper. I'm pretty sure they're better in some ways and worse in others. I just found it surprisingly difficult to reproduce their results using conventional approaches. So, sure, I believe they found what they found . . . but I call the result fragile, not robust.
Just for laffs, I re-ran the analysis including the duplicate cases:
subset3 <- election_year >= 1945 & election_year <= 2012 & abs(margin) < 10 & !living fit_1f <- lm(more_years ~ won + age + decades_since_1950 + margin, data=data, subset=subset3) display(fit_1f)
Which yields:
lm(formula = more_years ~ won + age + decades_since_1950 + margin,
data = data, subset = subset3)
coef.est coef.se
(Intercept) 74.65 3.18
won 3.15 1.89
age -0.91 0.06
decades_since_1950 -0.03 0.41
margin -0.19 0.17
---
n = 499, k = 5
residual sd = 10.93, R-Squared = 0.33
Almost statistically significant (whatever that's supposed to mean) with a z-score of 1.7, but still not in that 5-10 year range. Also it doesn't make sense to count a politician multiple times.
I thought I could get cute and remove age and decades_since_1950 and maybe something like the published paper's result would appear, but no luck:
lm(formula = more_years ~ won + margin, data = data, subset = subset3)
coef.est coef.se
(Intercept) 28.45 1.32
won 2.84 2.30
margin -0.12 0.20
---
n = 499, k = 3
residual sd = 13.32, R-Squared = 0.00
I tried a few other things but I couldn't figure out how to get that huge and statistically significant coefficient in the 5-10 year range. Until . . . I ran their regression discontinuity model:
df_m <- df_rdd %>% filter(year >= 1945, living_day_imp_post > 0) main_1 <- rdrobust(y = df_m$living_day_imp_post, x = df_m$margin_pct_1)
And this is the result:
Number of Obs. 1092
BW type mserd
Kernel Triangular
VCE method NN
Number of Obs. 516 576
Eff. Number of Obs. 236 243
Order est. (p) 1 1
Order bias (q) 2 2
BW est. (h) 9.541 9.541
BW bias (b) 19.017 19.017
rho (h/b) 0.502 0.502
Unique Obs. 516 555
=============================================================================
Method Coef. Std. Err. z P>|z| [ 95% C.I. ]
=============================================================================
Conventional 2749.283 873.601 3.147 0.002 [1037.057 , 4461.509]
Robust - - 3.188 0.001 [1197.646 , 5020.823]
=============================================================================
You have to divide by 365.24, but you get the picture. Then I looked above, and I saw the effective number of observations was only 236 or 243, not even as many as the 311 I had earlier!
So let me try re-running the basic linear model but just in the zone where the candidates were within 5 percentage points of winning or losing:
subset4 <- first_race & election_year >= 1945 & election_year <= 2012 & abs(margin) < 5 & !living display(lm(more_years ~ won + age + decades_since_1950 + margin, data=data, subset=subset4))
Here's the result:
lm(formula = more_years ~ won + age + decades_since_1950 + margin,
data = data, subset = subset4)
coef.est coef.se
(Intercept) 71.03 6.87
won 7.54 3.76
age -0.90 0.12
decades_since_1950 -0.36 0.78
margin -1.14 0.68
---
n = 153, k = 5
residual sd = 11.46, R-Squared = 0.31
Now we're getting somewhere! The estimate is 5-10 years, and it's 2 standard errors away from zero. We can juice it up a bit more by removing decades_since_1950 (a reasonable choice to remove) and age. We should really keep age in the model, no question about it, not including age in a remaining-length-of-life model is about as bad as not including smoking in a cancer model, but let's remove it just to see what happens:
lm(formula = more_years ~ won + margin, data = data, subset = subset4)
coef.est coef.se
(Intercept) 22.70 2.52
won 11.92 4.31
margin -2.00 0.77
---
n = 153, k = 3
residual sd = 13.34, R-Squared = 0.05
Wowza! An estimated effect of more than 10 years of life, and it's 2.8 standard errors away from zero. Got it!
So now we can reverse engineer, starting with the RD model from the paper and keeping only the first race for each candidate:
df_m_first <- df_rdd %>% filter(year >= 1945, living_day_imp_post > 0, first_race) main_1a <- rdrobust(y = df_m_first$living_day_imp_post, x = df_m_first$margin_pct_1) summary(main_1a)
which yields:
Method Coef. Std. Err. z P>|z| [ 95% C.I. ]
=============================================================================
Conventional 1482.670 1021.784 1.451 0.147 [-519.991 , 3485.330]
Robust - - 1.516 0.130 [-525.718 , 4115.893]
And then including age as a predictor:
main_1b <- rdrobust(y = df_m_first$living_day_imp_post, x = df_m_first$margin_pct_1, covs=df_m_first$living_day_imp_pre)
which yields:
Method Coef. Std. Err. z P>|z| [ 95% C.I. ]
=============================================================================
Conventional 819.480 708.968 1.156 0.248 [-570.072 , 2209.032]
Robust - - 1.051 0.293 [-740.342 , 2453.552]
So, yeah, the robust setting in this package doesn't matter much in this example---but the analysis is very sensitive to the bandwidth (yes, the bandwidth is estimated from the data, but that just tells us it can be noisy; the fact that something is calculated automatically using some theory and a computer program doesn't mean it's correct in any particular example) and to the decision of how to handle candidates with multiple elections in the dataset, and to the decision of how to handle the age predictor.
And here's the (ugly) code for the graphs I made:
loess_lost <- loess(more_years ~ margin, data=data, subset=subset & !won)
loess_won <- loess(more_years ~ margin, data=data, subset=subset & won)
loess_lost_fit <- predict(loess_lost, data.frame(margin=seq(-10,0,.01)))
loess_won_fit <- predict(loess_won, data.frame(margin=seq(0,10,.01)))
loess_all <- loess(more_years ~ margin, data=data, subset=subset)
loess_all_fit <- predict(loess_all, data.frame(margin=seq(-10,10,.01)))
ymax <- max(data$more_years[subset], na.rm=TRUE)
pdf("rdd_2a,pdf", height=4, width=6)
par(mar=c(3,3,2,1))
plot(data$margin[subset], data$more_years[subset], xlim=c(-10,10), ylim=c(0,ymax*1.02), bty="l", main="", xlab="Percentage vote margin", ylab="Days alive after election", xaxs="i", yaxs="i", mgp=c(1.7, .5, 0), tck=-.01, pch=20, cex=.5)
abline(v=0, col="gray")
mtext("Raw data", side=3, line=1)
dev.off()
pdf("rdd_2b,pdf", height=4, width=6)
par(mar=c(3,3,2,1))
plot(data$margin[subset], data$more_years[subset], xlim=c(-10,10), ylim=c(0,ymax*1.02), bty="l", main="", xlab="Percentage vote margin", ylab="Days alive after election", xaxs="i", yaxs="i", mgp=c(1.7, .5, 0), tck=-.01, pch=20, cex=.5)
abline(v=0, col="gray")
lines(seq(-10,10,.01), loess_all_fit, col="blue")
mtext("Raw data with loess fit", side=3, line=1)
dev.off()
pdf("rdd_2c,pdf", height=4, width=6)
par(mar=c(3,3,2,1))
plot(data$margin[subset], data$more_years[subset], xlim=c(-10,10), ylim=c(0,ymax*1.02), bty="l", main="", xlab="Percentage vote margin", ylab="Days alive after election", xaxs="i", yaxs="i", mgp=c(1.7, .5, 0), tck=-.01, pch=20, cex=.5)
abline(v=0, col="gray")
lines(seq(-10,10,.01), loess_all_fit, col="blue")
lines(seq(-10,0,.01), loess_lost_fit, col="red")
lines(seq(0,10,.01), loess_won_fit, col="red")
mtext("Raw data with separate loess fits", side=3, line=1)
dev.off()
P.P.S. This was all a lot of work. I did it because it's worth doing some work now and then---but don't forget the larger point, which is that we knew ahead of time not to trust this result because of the unrealistically large effect sizes, and we knew ahead of time not to think that causal identification + statistical significance + robustness tests = discovery, because we've been burned on that combination many times before.
To put it another way, don't think that you should give the claims of a published or preprinted social science study the benefit of the doubt, just because someone like me didn't bother to go to all the trouble to explain its problems. The point here is not to pick on the authors of this particular study---not at all. They're doing what they've been trained to do.
P.P.P.S. Again, nothing special about regression discontinuity here. All the same concerns would arise with any observational study, with specific concerns arising from regression, difference in differences, nonparametric modeling, instrumental variables, synthetic controls, etc. The same problems arise in experiments too, what with issues of missing data and extrapolation. The particular problems with regression discontinuity arise when (a) people naively think that causal identification + statistical significance = discovery, and (b) people take robustness tests, placebo controls, etc., too seriously. Alternative analyses are part of any good statistical study, but generally the point should be to explore and understand the limitations of one's conclusions, not to rule out alternative explanations. And, with all these kinds of study, if the underlying effect size is small and your measurements are noisy, you're drawing dead (as they say in poker). Again, this can happen in any study, ranging from a clean randomized experiment at one extreme, to a pure observational study on the other.
You might say that I'm shooting a rabbit with a cannon here. The research and writing of this post took me something like 10 hours! That's a lot of time to spend on an effect that I think is small, highly variable, and essentially undetectable.
My reason for writing this post is because I'm concerned about the general attitude that causal identification + statistical significance + robustness study = discovery. For my own purposes, I didn't feel the need to reanalyze the data---the problems were all clear to me from the beginning---but I put in the time to do all this to make it clear what's going on, to people who haven't been steeped in thinking about low power, forking paths, and all the rest. I'm hoping that the effort I put into taking apart the claims in this particular paper can be abstracted in some way so that my colleagues and I can write something more general that can help many researchers in the future. This is a path we often take in applied statistics: working on a single example in detail to develop more general methodological conclusions. Usually we think of this as doing an exemplary analysis that can serve as a template for future workflow and an inspiration for future methods; in this case it's more of an exploration of what can go wrong. But that can be important too.
My goal is not to "debunk" the claims in the paper under discussion; rather, my goal is to understand what went wrong, as a way of figuring out how we can all do better in the future.
P.P.P.P.S. OK, one more thing. This is for those of you who (a) have read this far, and (b) want to say something like this to me:
Hey, destructive statistician. Stop with your nihilism! The authors of this peer-reviewed paper did a very standard, reasonable analysis and found a large, statistically significant, and robust effect. All you did was perform a bunch of bad analyses. Even your bad analyses uniformly found positive effects. They just weren't statistically significant, but that's just cos you threw away data and used crude methods. It's well known that if you throw away data and use inefficient statistical analysis, that your estimates become more noisy, your standard errors become larger, and your power has gone down.
tl;dr. You, Gelman, maligned a competent, high-quality paper---one that passed peer review---by the simple expedient of re-running their analysis with fewer data points and a noisier statistical method and then concluding that their results were not statistically significant. Ironic that you, Gelman, did this tactic, given how disparaging you usually are about using statistical significance to make decisions.
The above response sounds kinda reasonable---indeed, some of you might agree with it!---and it has the form of a logical argument, but I think it's wrong, for several reasons.
First, regarding the point that the coefficient shows up positive in all my analyses, hence making this nothing more than a dispute over statistical significance:
This where it's helpful to have a Bayesian perspective---or, if you'd prefer, a design-based perspective. It goes like this.
Second, regarding the idea that I've replaced their state-of-the-art RD analysis with various low-power linear regressions:
Actually, no. The robust adaptive RD analysis does not have higher power or more statistical efficiency than the linear model. These are just different models. Indeed, the decision to not include age as a predictor lowers the power of the analysis. Regarding sample size: I took out the duplicate elections featuring the same candidate because it's inappropriate to consider these as independent data points; indeed, including them in that way can just give you artificially low standard errors. (I think it would be easy enough to show this using a bootstrap analysis or something like that.) The real point, though, is you can't tell much about the power of a study by looking at the z-score or statistical significance of a coefficient estimate.
P.P.P.P.P.S. Wow---the above post is really long. And I don't remember writing it at all. That's what blog-lag will do to you!
P.P.P.P.P.P.S. One of the authors, Erik Gahner Larsen, responds here; I respond to his response here.
In his response, Larsen notes that we had an email exchange about the article. I'd forgotten about that. At the time, I'd planned to append some of that exchange to my post. So I'll do that now. The exchange is from January.
Larsen:
I will need to read the blog post in greater detail but not to keep you (or my co-authors) waiting, I have a few initial thoughts. Do let me know if I have missed something specific you would like for me/us to comment on (or/and if I misunderstood your points). In brief, I am happy to see that you don't question our honesty and transparency, and I have no issue with you publishing the post as it is.
You bring up a lot of sensible points. To estimate the LATE requires a lot of data and we do not have a lot of data. For that reason, and - ironically (and you might disagree) - to not run the risk of forking paths, we kept the identification strategy and the models as parsimonious as possible (i.e. to leverage as much data as possible). For example, as you discuss the bandwidth choice in your post, we report the results under different bandwidths and show that the main result is sensitive to the choice of bandwidth (and that it is possible to 'kill' the effect, cf. Figure 1 in the appendix material). Again, do let me know if I misunderstand your point here (maybe it's easier to understand when formulated in relation to type M and type S errors?)
If the "true" effect is, say, .5 years, we would need a lot more data to detect that. In other words, I believe your point 4 is spot on. That's indisputable and simply a limitation of the paper. I am not sure I would say that the paper is 'fatally flawed' for that reason, but I get the point. Are you saying that we might as well have detected a negative effect of 5-10 years? (I mean, if we're simply playing around with noise here.) In any case, and with the risk of sounding morbid, we will have less missing data in the future and hopefully, in a distant future, have sufficient statistical power to detect a more reliable effect.
From what I can see, point 1, 2 and 5 are all related to the point of the effect size being huge/unrealistic/silly. 5-10 years is indeed a huge amount of lifetime. For that reason, I am not surprised that people find it important to reproduce the findings and I expected that people would do this. We had a lot of discussions about the effect size when writing up the paper and, to be honest, I don't know what's a realistic/common sence effect size to expect here. When you work on a paper long enough, your results become 'common sense' (or to paraphrase Duncan Watts... 'everything is obvious once you know the answer'). My prior is also that the closer an effect size is to 0, the greater the probability that the finding will replicate (cf. your point 2).
For the point: "I also noticed some data problems, such as cases where the politician's death date came decades before his election. There were a bunch of these, for example see here:"
I will have to look into the specific data points in question, but to make sure that we didn't have any specific problems with the analysis, we filtered the sample to only include politicians alive after the election (and thus not include politicians that died before the election for that particular election).I am not sure I agree that we would argue that 'losing a close election really did kill these candidates for governor'. I might misunderstand your point here but we've had a lot of discussions about this as well -- this one also with the reviewers. I am not convinced that we can use the data to reach that conclusion, or as wrote in the response letter to a reviewer: "In brief, it is difficult to establish a counterfactual life expectancy based on data from non-politicians. Politicians and non-politicians differ or various dimensions including but not limited to family background and network composition. Consequently, we have limited data that will provide credible answers to whether losing an election causes a premature death." We have tried our best not to make such interpretations in the paper but maybe we should've been more explicit about what can be concluded (and not) based on the data (the 4,000 word limit was not friendly to us here).
An easy clarification: Harvard Dataverse show .csv files as .tab. If you click "Download" on the file, you should be able to select "Original File Format (Comma Separated Values)".
I would lie if I said that I was happy to hear from you, so I will not pretend to be happy. That being said, my initial thought when I read your mail ("garden of f**king paths!") is, upon thinking about this and replying to your mail, being replaced by an optimism that this will lead to an interesting post/discussion on effect sizes and sufficient statistical power in RDD studies.
My reply:
Thanks for the quick reply. There was not any particular item in the post that I was asking for feedback on; I just wanted to share with you.
Regarding the type M and type S error thing: Yes, it's as you say, I suspect any true effect would be much less than 5 years, so that a pattern in the data that shows up in the regression is basically just noise. I think that in a replication study of other data with the same sample size, for example from some state legislatures or whatever, it would be possible to get an estimate of -5 yrs or -10 yrs. I expect that a fully preregistered study would not yield a statistically significant result, but your study was not preregistered (nor are most of mine! I'm not holding my own research up as a model here), and I think that, just as in the "50 shades of gray" paper, it's possible to fool yourself with forking paths without ever realizing it.
Is an effect size of 5 or 10 years reasonable? I agree that we can't know, but it really doesn't make sense to me, especially given that candiates typically face many elections in their lifetimes. The point of the type M errors is that, with such a small sample and such noisy data, anything statistically significant estimate you will find will _have_ to be huge. So, in that sense, I don't see your estimate of 5-10 yrs as providing any useful information regarding the magnitude of the effect: Even it turns out that there is some average effect, even as large as 1 or 2 years (which I would really doubt), the obsrved estimate of 5-10 yrs is an artifact of the small sample and high variability.
Regarding the data problems: Yes, I did check that they went away in the subset of recent elections, so I didn't investigate them carefully. I'm guessing these were data entry errors.
Larsen added:
Also, a good friend of mine informed me (when he saw the study) that we're not the first to show an interest in this subject. Apparently, a couple of economists published a study on the topic in 2019 as well. They find a positive effect but a lot smaller, i.e. ~3 years when looking at elections post-1908. Interestingly, they find that governors running in elections post-1908 (the sample most similar to ours) live ~6 years longer (Panel B, Column 1-2, Table 3). I am not linking to this study to make a point about the results (again, I believe you have a good point on the fact that we would need more statistical power to estimate a smaller effect), but it might be of interest to cite that study as well to make a broader point about inference and robustness?
My bad for not remembering to add this conversation to the post.
P.P.P.P.P.P.P.S. I made tiny changes in the code to improve the readability of the axes and fix the y-axis labels in my graphs.
“1. Common sense”
+1000 This is the first thing that struck me when I started reading this blog and the examples of studies like himmicane, ESP, etc. They all fail the initial common sense test.
I appreciate all of the work that went into this post! It is a great demonstration. It seems necessary to ‘show’ people this, but I think the critique of many of these studies could just stop after point #1.
Thank you for engaging with our paper. I reply to your points in this blog post: https://erikgahner.dk/2020/a-response-to-andrew-gelman/
I would like to thank you for getting engaged in the discussion and then giving us a very good example of scientific debate.
+1
Dear Prof. Gelman, dear authors thanks a lot for the stimulating scientific discussion!
I learnt a lot out of it! Enormous thanks!
The article reminded me a famous way of saying of a famous Italian politician names Giulio Andreotti that I just wanted to share
https://it.wikipedia.org/wiki/Giulio_Andreotti
Andreotti used to say “Power wears out those who don’t have it…” (“il potere logora chi non ce l’ha…”)
You fundamentally misunderstand the idea of a forking path. You seem to be under the impression that the objection is that one cannot reproduce statistically significant result, and complain that Gelman tried different analyses until he got insignificant results.
> Andrew Gelman played around with the data till he got the insignificant finding he wanted and then he decides to attribute effects consistent with those in the paper to ‘just for laughs’ or by ‘including data’ (that was not excluded in the first place). What is the difference between selecting “the most natural predictors” and including variables just for laughs? Garden of forking paths, I guess.
That’s exactly the point. That someone CAN p-hack in both directions, producing statistically significant and statistically insignificant results depending on what they want to see, is the problem here.
Also, I think you’re missing something about RDD:
> Specifically, the figure shows a statistically significant effect but it is clear that we cannot observe this effect. I do still believe it is relevant to look at the raw data to get a sense of what we are looking at, but I am not sure why our evidence is less compelling just by looking at the raw data.
The point of RDD is that you get a sort of local random assignment from the conditional-continuity-in-covariates assumption. Here, that assumption means believing that having more votes has a strong negative association with lifespan. If you don’t believe more votes generally means shorter lifespan, you cannot believe winning means a longer lifespan, since the latter is entirely driven by the former.
Erik:
You write:
1. I was not “very selective in what I reported.” I was not selective at all. I reported the analysis that I did.
2. It’s not clear to me what “engaging with an open mind” should mean. Your paper makes an implausible claim that does not show up in the data (see second plot in the above post). But I could figure out how your result could arise as an artifact of an overfit regression analysis (see fourth plot above).
Does “engaging with an open mind” mean that I should, by default, believe a claim that is published, has an identification strategy, and has statistical significance? Many people seem to think so. To me, “engaging with an open mind” is to start with the claim and the data and work from there.
3. You write that I “invested a non-trivial amount of time.” That’s fine! I’m sure you and your coauthors invested a non-trivial amount of time in this project too.
4. You write that I built up a “false” narrative. If there is anything in my post that is false, just let me know and I’ll correct it.
To continue:
You write:
I agree 100%. Open discussion is the best.
You write:
Fair enough. We can disagree. Different people look at the same evidence and come to different conclusions. I look at the second through fourth graphs above and come to one conclusion, you look at the top graph and come to another. There are lots of different ways of looking at the same data.
You write:
That theory of yours is false!
You write:
I think you’re italicizing “saying” to suggest that what I said is not what I did. But what I said is what I did.
You write:
No, it’s the opposite. As I wrote in the above post, I had to work quite a bit to get the statistically significant finding. The order of the analyses in the post is the order that I did them.
You write:
I agree. 5 years of life is a huge effect! I don’t think your data show such an effect, which makes sense, given its implausibility. Or, to put it another way, I think that the data are consistent with an average treatment effect of 5 years, but they’re also consistent with an average treatment effect of 0.
You write:
That’s good. You can’t prove something false!
Also, we’re in agreement about my code. I described it as “ugly” and you describe it as “how people wrote R code in the 90s.” Actually, back in the 90s I was writing in S, not R, but, yeah, we’re in agreement that it’s not pretty.
tl;dr. There are many ways of analyzing these data. Some analyses find this strong effect and some don’t. As I summarized above, the result is very sensitive to the bandwidth (yes, the bandwidth is estimated from the data, but that just tells us it can be noisy; the fact that something is calculated automatically using some theory and a computer program doesn’t mean it’s correct in any particular example) and to the decision of how to handle candidates with multiple elections in the dataset, and to the decision of how to handle the age predictor.
Regarding the issue of multiple elections per candidate in the data: Each politician has only one life, so I don’t think it makes sense to include these as independent data points. If I were doing a full analysis, I might handle this using a multilevel model; I’d also want to handle missing data using some sort of survival analysis and be really careful about the age variable, as the biggest predictor of future length of life is how old you are now. But ultimately I don’t think these data will allow you to estimate what you’re trying to estimate here: the data are just too noisy given plausible effect sizes. Yes, you found a large effect, but that comes from the statistical significance filter: with a small noisy data set, any effects you find will be large. That’s what I refer to as a “design-based perspective.”
Thanks! And my apologies for the ‘ad-hominem type attacks’ (as pointed out by A.J. Mafolasire) and speculations. As for your blog post, there was a lag between when it was written and the publication date. When writing up the blog post, I found it too good to be true that you was unable to get the significant results from the get-go. I believe that you engaged with our paper with an open mind (i.e. not determined to find insignificant results but to examine what the data would show — not to uncritically believe a published finding).
Just adding my thanks for your own openness in engaging here.
I think most of us are just trying to do the best we can with what we’ve got. But “what we’ve got” and “the best we can” both evolve and improve over time as a result of thoughtful criticism and, perhaps most important, thoughtful responses.
Erik:
How did you treat multiple observations for the same candidate?
Did you consider them independent?
After filtering year >= 1945 and margin < 5, there are about 40 duplicated candidates.
For this reason, Andrew approach of using first_race is reasonable. At least, that removes the problem of correlated measures.
Not sure if it’s correct (please correct me if I’m wrong) but using a random intercept with ID = {cand_first, cand_last}, these two models are identical
df_m %
filter(year >= 1945 & living_day_imp_post > 0 & living==”no”) %>%
mutate(won = ifelse(margin_pct_1 > 0, 1, 0),
margin = margin_pct_1) %>%
filter(abs(margin) %
mutate(id=factor(str_c(cand_first, “_”, cand_last)))
mdl %
lmerTest::lmer(living_day_post ~ won + margin + year + ex + female + (1|id), data=., REML=FALSE)
mdl_control %
lmerTest::lmer(living_day_post ~ year + margin + ex + female + (1|id), data=., REML=FALSE)
> lmtest::lrtest(mdl, mdl_control)
Likelihood ratio test
Model 1: living_day_post ~ won + margin + year + ex + female + (1 | id)
Model 2: living_day_post ~ year + margin + ex + female + (1 | id)
#Df LogLik Df Chisq Pr(>Chisq)
1 8 -2318.6
2 7 -2318.8 -1 0.2177 0.6408
IIRC we did not pay attention to multiple observations for the same candidate. I am not saying it’s not important — only that we most likely didn’t consider it.
When I tweak the code in the blog post for the simple linear model (i.e. the Gelman and Hill approach) and only take one election from each candidate, I get an estimate of 4262 days (s.e. 1546 days).
Here is my code:
df_rdd %>% filter(year >= 1945, living_day_imp_post > 0) %>% mutate(won = ifelse(margin_pct_1 >= 0, 1, 0), margin = margin_pct_1) %>% mutate(id = paste0(death_date_imp, "-", cand_last)) %>% group_by(id) %>% mutate(election = seq_along(id)) %>% ungroup() %>% filter(abs(margin) % with(lm(living_day_imp_post ~ won + margin)) %>% broom::tidy()Including age as a covariate (i.e. living_day_imp_pre) returns an estimate of 2660 days (s.e. 1344 days). Also, when I run the same analysis with rdrobust I get an estimate of 2749 days (s.e. 873 days). 1948 days (s.e. 701 days) when controlling for age.
Not sure what is happening with the formatting of the code (it should say: filter(abs(margin) %). I’ll try again:
df_rdd %>%
filter(year >= 1945, living_day_imp_post > 0) %>%
mutate(won = ifelse(margin_pct_1 >= 0, 1, 0),
margin = margin_pct_1) %>%
mutate(id = paste0(death_date_imp, “-“, cand_last)) %>%
group_by(id) %>%
mutate(election = seq_along(id)) %>%
ungroup() %>%
filter(abs(margin) %
with(lm(living_day_imp_post ~ won + margin + living_day_imp_pre)) %>%
summary()
broom::tidy()
I’m giving up… here it is: https://gist.github.com/erikgahner/39212cf46422e3871ba99873ccba45ac
No worries, I’ve been able to get your code :)
Unfortunately, it seems that the website likes eating symbols… :D
Removing one election race is not the optimal strategy IMHO. Or at least, there should be a justification for choosing one specific race.
The fact that one candidate who both won and lost a race has the same life span should make you reflect on the effectiveness of the causal relationship. At least, you should describe which election is the one that influences the candidates’ life span. The last one or the first one?
This is important because if you consider the same candidate with won=0 and won=1 and apply a hierarchical model, his linear model (only won covariate) is horizontal flat. This affects the population-level slopes a lot.
I agree. There are several ways we can analyze the data and I am not saying we should remove any candidates from our data. My point was simply that I am not sure this can explain the discrepancy between our results and what is being presented above.
In appendix 3.4, we run the analysis on elections with open seats: “We assess the validity of our results when we use only the sample of candidates from elections for open seats. This guarantees that none of the candidates appear more than once in the dataset, and that the sample of candidates include only candidates who have not been elected governor before. Table 5 reports the results when estimated on this restricted dataset. As can be seen from the table, making this sample restriction does not alter the results substantially although there is less statistical power.”
I like the idea of exploring within candidate variation in election outcomes, but I will need to think more carefully about what such estimates will tell us (and how exactly to model this) before I would make any inferences.
Erik:
I surrounded your code by “pre” tags in html to get it to format.
Hi Eric,
I think Andrew raises valid points, and I understand why you are vigorously defending your work. However, based solely upon your code you posted on the Github (“erikgahner/Code to Paolo Inglese”) and some poking around in my own R code using package “brms” (Bayesian Regression Modeling using Stan”) by Paul-Christian Burkner, I’ve come to the conclusion that the effect of “won” on “living_day_imp_post” you’re seeing is simply an artifact due to the functional relationship between “won” and “margin” — the former merely being a discretization of the latter.
Narrowing the dataset to “margin” values of magnitude less than 5 really accentuates the correlation between “won” and “margin”.
The simple regressions I performed gave opposite signs for the coefficients estimated for “won” and “margin”. Plus, the “pairs()” plots of the posterior samples of these coefficients from the estimated model (`formula = living_day_imp_post ~ won + margin + living_day_imp_pre`) also had high negative correlation in the bivariate scatterplot.
So I just took the posterior samples of these coefficients, say b_won & b_margin, multiplied them by the dataset terms won & margin respectively, and added them together to get the contribution that won & margin make to the prediction of living_day_imp_post. I then plotted boxplots of these contribution for won=0 and won=1. The distributions show large overlap — I’m sure a formal statistical hypothesis test of these contribution distns would not reject the null hypothesis that the contribution of won & margin together are the same for won=0 and won=1.
I went further with models that used either one or the other of the terms won and margin, each yielding coeffs with posterior distribution that largely overlapped zero, and I compared the “loo” metrics (elpd) between the model and found that although the model with both terms gave a larger elpd, it was within 1 std. error of the elpd’s of the two models using either of the terms.
But, I think the clearest indication that there is no real predictive power of won on living_day_imp_post is the fact that even the model that shows a highly significant coefficient for won ends up having a highly significant negative coefficient for margin and that the total contribution of these terms is basically the same whether won=0 or won=1.
I hope this helps.
Hi Michael,
Thank you for the response. To reiterate, I am not arguing that the (simple) code used to get these coefficients is the best approach — and it is not something we report or use in the paper. My point was that it’s not necessary to use our replication material (or the rdrobust package) before you will find any significant results (though this was the case for Gelman) – and even the most simple approaches (e.g. the introductory procedure outlined in Gelman and Hill, 2007), will yield significant results.
It sounds like an interesting approach (i.e. the Bayesian analysis on the observations below abs(marg) < 5) and I will be happy to look at your results. Is the code publicly available?
Erik
Eric,
I’ve posted the code to my github repository: [here](https://github.com/apollostream/Longevity_Elections)
Feel free to explore, and let me know if you have any questions.
Thanks, Michael! Much appreciated. I have saved a local copy and I’ll go through the data and output. I’ll let you know if I have any questions or anything meaningful to add.
I’m a little late to this post. Have you considered updating your post, with a P.S. or something, noting the baseless speculations or removing them entirely, otherwise they’ll always be on your blog and your apology will be buried in the comments section of this blog..
Andrew:
What do you make of Erik’s criticism that if you had just started with the recommendations from your own textbook (Gelman and Hill, 2007) that you would have replicated the key result right off the bat? That criticism seems to speak against your claim that it was hard to replicate the key result.
Anon:
My views have changed a lot since 2007! Nowadays, I’d always want to include relevant predictors such as age. Also, I never would treat multiple observations on the same candidate as multiple data points.
Very hard to take the arguments seriously with the ad-hominem attacks
He apologized.
Please consider that we are all humans, and getting your work criticized by a big name in Stats, as Andrew is, is tough. Also, Erik has been very nice joining the comment section and getting the feedback in a very constructive way.
Yeah, well written, but I think it could do without a few ad-hominem type attacks here and there. It could still have been a strong response without some of the snarkiness.
Kudos for an open response.
I tried the links and the paper seems to be behind a paywall. In the paper do you provide a potential explanation as to why losing a close election would cause such a dramatic decrease in lifespan?
In your post you acknowledge the large effect and that people should be skeptical, but you seem to dismiss ‘common sense’ slightly by saying, “Accordingly, I am not sure how strong of an approach common sense is (in and by itself) when we are to evaluate effect sizes.” I think it might be a good guide that something is amiss.
Suppose someone presents you with a strategy for estimating the following quantity, which you judge to be sound:
theta =
limit as z approaches z* from above of E[Y | Z = z]
minus
limit as z approaches z* from below of E[Y | Z = z]
where Y is the observed response, Z is a predictor, and all and only units with Z greater than or equal to z* receive the treatment. Suppose further that:
(Semi-continuity)
E[Y(1) | Z = z*] = lim as z approaches z* from above of E[Y(1) | Z = z]
and
E[Y(0) | Z = z*] = lim as z approaches z* from below of E[Y(0) | Z = z]
where Y(1) is the potential response when a unit is treated, and Y(0) the potential response when it isn’t.
It follows that the estimation strategy is thus a sound estimate of:
E[Y(1) – Y(0) | Z = z*]
which is the average treatment effect in the cutoff population.
The question I have is where you think the failure is occurring. Is it:
(1) You think the typical estimator of theta is not sound;
(2) You think semi-continuity doesn’t typically hold;
(3) You think the average treatment effect in the cutoff population is a problematic estimand;
or all of the above?
Note that my question here is less about your problem with this specific paper, and more about your general problem with regression discontinuity papers in general.
The right way to estimate these models is to fit a flexible basis function set to the data ensuring that the expansion is capable of representing a rapid change in level across the particular boundary of interest. Then look to see what the posterior fit actually *does* show.
A useful representation for problems of this type is something like a polynomial of moderate degree + a smooth step function like an inv_logit…
you can do this using least squares with something like:
s = .5
lm( y ~ 1+x+x^2+x^3 + inv_logit(x/s), data = mydata)
Then look at the size of the jump.
If you do this with this data set you will undoubtedly get a trivially small jump.
However, if you fit two separate models to the data before x =0 and the data after x=0 then you will get a jump almost every time… even if there is absolutely nothing going on:
I showed this in simulation back in January (OMG with COVID, it now seems like it was years ago!)
http://models.street-artists.org/2020/01/09/nothing-to-see-here-move-along-regression-discontinuity-edition/
The problem is simply that by fitting two separate models you are asserting that no information from across the boundary could be useful for accurately assessing the value of the function near the boundary. This is essentially equivalent to assuming that the function is discontinuous across the boundary. So the analysis assumes the thing it was setting out to ask.
OK, so I think you’re saying that your objection is to (1) in my list, and not (2) or (3). Is that right?
I’m wondering if Andrew takes the same position here.
I’ll have to think more about your proposal, but given that the goal is estimating theta in my formulation, and given that theta is expressed in terms of one-sided limits, don’t you agree there’s something funny about using data to the right of the limit to estimate the left-limit, or using data to the left of the limit to estimate the right-limit?
If you agree that the function *could* be a completely smooth function where nothing is going on at x=0 and also *could* be a function that changes behavior dramatically in the vicinity of x=0 then you need to use a family of functions that can represent both extremes and things in the middle. Instead of thinking about this as “using data to the right of the boundary to estimate the function to the left of the boundary” think of it as “using *all the data* to estimate a function whose behavior can vary widely across this boundary” when you think like this its not at all confusing. You are not trying to fit *two* functions, you are trying to fit *one* function of x.
We want to use an estimator that can recover functions that do, and functions that don’t, have discontinuities at the cutoff. It isn’t a question of “changing dramatically”, as this could happen in a continuous fashion. An estimator that enforces continuity at the cutoff is not going to be able to recover a function that does have a discontinuity at the cutoff. And the point of my derivation is that if we think the average treatment effect in the cutoff population is nonzero, and we think the potential regression functions are semi-continuous, then there is a discontinuity there. So you need to use an estimator that allows there to be a discontinuity there, otherwise under semi-continuity you’re assuming there is no average treatment effect in the cutoff population.
I feel like you’re thinking in terms of picking a family of functions that contains the “true model” where a discontinuity is there or not there, and statistics tells you if the discontinuity is real or not real. Daniel is saying to pick a set of functions that might not contain a “true model” where there’s a “real” jump discontinuity, but can approximate such discontinuities to an arbitrary sharpness if there’s strong evidence for it. With a set of smooth basis functions including inverse logit, if there’s enough evidence for a discontinuous effect at x=k it’ll still look very close to a discontinuous jump as k goes to infinity.
It might be true that picking a basis of smooth functions where “the true effect” is discontinuous biases your effect size downwards relative to the non-parametric local linear RDD, but you get a pretty dramatic variance reduction in return. People sometimes argue that unbiasedness of an estimator is a minimal requirement, but personally I find that an estimator like the NPRDD that’s so unstable that it’s nearly guaranteed to see large effects in pure noise is much less useful.
If you need an estimate of the “average treatment effect”, it can just be the coefficient on the logistic step function in Daniel’s example. That gets iffy if the curve turns out to be pretty shallow, but in that case you should be asking if you have proper causal identification in the first place.
I’m all for regularization, but I generally want the bias to disappear as the sample size gets larger. If the model enforces continuity, the bias never goes to zero, so the estimator is inconsistent. Seems less than ideal.
Again, the point here is that if semi-continuity holds, and if there is a nonzero average treatment effect at the cutoff, then there is a discontinuity in the regression function. The size of that discontinuity is precisely the size of said treatment effect. If we’re using a model that assumes that there is no discontinuity, then the model is assuming said treatment effect is zero. Let’s not lose the plot here.
> Again, the point here is that if semi-continuity holds, and if there is a nonzero average treatment effect at the cutoff, then there is a discontinuity in the regression function. The size of that discontinuity is precisely the size of said treatment effect. If we’re using a model that assumes that there is no discontinuity, then the model is assuming said treatment effect is zero. Let’s not lose the plot here.
That’s the same as a logistic function as k -> infinity, so you can get an approximate estimate of the treatment effect if the data is convincing of a discontinuity and fits to a high k. It’s true that using smooth functions makes it categorically impossible to estimate the true function with any finite sample, but
1. There is no true model, they’re all wrong anyways
2. Even if there is a true model, and your family of functions includes it, you’re almost surely not going to estimate the true function with a real sample. The only thing that matters is how wrong you are.
> I’m all for regularization, but I generally want the bias to disappear as the sample size gets larger. If the model enforces continuity, the bias never goes to zero, so the estimator is inconsistent.
As n goes to infinity, the logistic function should go to a step function. Unless I’m missing something, it is asymptotically consistent, just biased. Which is fine, I don’t think unbiasedness is lexicographically preferred to low variance, and I think the variance of NPRDD is too high to be useful.
as “somebody” said, the function
inv_logit(x,q) = 1/(1+exp(-x/q)) goes pointwise to a step function *everywhere* except *exactly at x=0* as q goes to zero (or you can do 1/(1+exp(-kx)) as k goes to infinity)
So simply define your treatment effect as f(x+epsilon) – f(x-epsilon) for epsilon finite and small… and you recover this definition of the treatment effect in the limit of large data.
somebody, Daniel:
I think what you’re saying is that instead of estimating the size of the discontinuity, we should instead estimate the difference between the asymptotes of a certain sigmoid, which is constructed as a smoothing device in place of the discontinuity. And the tuning parameter that controls the smoothness of the sigmoid can be set to decay as the sample size increases such that asymptotically it becomes a step function and the estimator converges to the discontinuity. Do I have that right?
I think this is a pretty reasonable idea for regularization. Do you have a specific way of setting this tuning parameter to ensure the smoothing diminishes at the right rate for the estimator to converge to the average treatment effect at the cutoff? Just having it decay doesn’t guarantee the estimator is consistent. Maybe some type of cross validation would do the trick.
In any event, if insufficient smoothing of the estimate of the discontinuity is the whole of the issue, then that means the problem with RDD is (1) from my original post. And that’s clarifying, though I have to admit that a lot of what Andrew complains about doesn’t seem to be covered by this complaint.
I should just say for the record I’m neither pro-RDD nor anti-RDD. My view is just that RDD has a logic to it, and if you want to criticize it you should tell us where the logic is failing in any given case. It’s frustrating to read posts like this from Andrew because I can’t figure out what he’s disagreeing with, since he won’t express the complaints in terms of RDD logic. But I think this sub-discussion has been illuminating, in that it’s clear that this specific complaint is about insufficient regularization of the typical estimators used.
If you make the scale of the sigmoid on the same order of magnitude as the measurement error in your x values you should be fine for all practical purposes… Asymptotic consistency is basically unimportant in most real world scenarios where the number of data points is always less than 100 trillion, usually less than a few thousand.
The phenomenon is similar to so called “asymptotic series” these are series representations of functions that diverge as the number of terms increases, but for a finite number of terms they’re often far more accurate approximators of functions than convergent series.
So, in your example, you’re talking about percentage points in an election. When we look at something like the Bush / Gore election and the whole issue of hanging chads and soforth it became clear that we really can’t count elections meaningfully more accurately than about 3 maybe 4 significant figures. So using something like 1/(1+exp(-x/.05)) where x is expressed in percentage points is as sharp as you could ever really be just due to the x value measurement uncertainty.
You can usually make a similar argument in any other RD context.
Also, I just don’t work in the p value / null hypothesis testing framework. So for me I’d probably make the scale a parameter and provide a prior over how sharp it should be.
Daniel,
Getting the convergence rate right is important if we want to be able to build confidence intervals around this estimator with correct large sample coverage. I realize you’re less interested in this kind of frequentist property, though I suspect that a well specified fully Bayesian approach here will be asymptotically equivalent to some sort of cross validation for choosing the tuning parameter. A fixed tuning parameter will lead to asymptotic bias, and will result in confidence intervals to have less than advertised coverage (or, if you like, hypothesis tests have higher than advertised type I error rates).
But in any case, I think this is productive. I agree that there is room for improvement in how we estimate the discontinuity, and I think this points to a clever way to achieve such an improvement. I just don’t think this is what Andrew is unhappy about (or not the only thing he’s unhappy about), since I somehow doubt he’d be happy with many RDD papers if they just used this estimator instead of the usual one.
As soon as you make a realistic accounting of measurement noise in x, there is no converging in sharpness to below the scale of the measurement error. If you pretend the measurement error in x is exactly zero you can do the math, but it’ll be wrong anyway.
Still, I’m just glad you understand that you can treat a step function as a particularly sharply changing continuous function, and I hope you explore that avenue in your models!
For me, this is one of the better explanations of what’s going wrong with lots of RD analysis. Thank you.
I have a response awaiting approval. But to that response I’d add that the formulation of the goal as estimating theta in your formulation is artificial. What you really care about is “did something important happen around x=0?” and there are many ways to formulate that mathematically. A formulation which essentially assumes discontinuity and then discovers evidence that discontinuity exists is begging the question (https://en.wikipedia.org/wiki/Begging_the_question), and this is essentially what the RD framework does.
I’ll await your response, but I think there’s nothing artificial about it. What we’re after in these studies is the average treatment effect in the cutoff population. This is an estimand expressed in terms of latent random variables, namely the potential outcomes. To estimate it, we have to first translate it into an estimand expressed in terms of observed random variables. This is what the semi-continuity assumption allows us to do, and it results in the estimand being expressed in terms of the left and right limits of the observed regression function at the cutoff.
Now maybe you think this is a bad estimand to target, in which case you’re asserting (3). Or maybe you think there’s a different assumption we should make instead of semi-continuity that allows us to express this without right and left limits. In that case you’re asserting (2). But if you don’t assert (2) or (3), then you must be asserting (1) if you think there’s something problematic with a given application of RDD.
I can’t speak for Gelman, but the failure to me is in the mindset implied by asking if “semi-continuity typically does/doesn’t hold”. I don’t care if it typically does or doesn’t hold. I want to see people interrogating whether or not it holds in the dataset under study every single time, and they often don’t.
Of course. It’s an assumption, and sometimes it will hold and sometimes it won’t, and you have to make the case that it does if you want to get this off the ground. I say “typically” here because Gelman typically thinks these studies are unconvincing, and so I’m assuming 1, 2 or 3 (or some combination) are typically present in Gelman’s view. But I agree that it’s all case by case, and don’t take any position on the present paper as I haven’t investigated these issues carefully in this case.
I think that there is a tendency among econometricians to not make the case for assumptions and proceed as if as long as one can formulate the problem with a particular causal identification strategy, then the assumptions come for free. I want to see critical evaluation of plots, but in applied economics papers I typically just see a text description of the method and then the outputs presented as numbers. Not referring to this paper specifically, just in general.
If that’s true as a general statement, that’s fair criticism, but it would seem to apply to any scenario where an approach is used without its assumptions being scrutinized. I suppose the claim is RDD is unique in the deference it receives from applied microeconomists? I can’t comment on that myself, though I am aware that this has been repeatedly disputed in prior threads on this topic by practitioners in the field.
“we don’t have to follow Kahneman’s now-retired dictum that “you have no choice but to accept that the major conclusions of these studies are true.””
No, but we also have to consider whether your examples and much of modern behavioral science reflect any “major conclusions” in the first place. A lot of these studies are looking for effects that are more “cute” or “newsworthy” than major. They might get your citation count up enough to make tenure, and might get the university press office to push some media your way, but major? let’s repeat this list:
“beautiful parents were 8 percentage points more likely to have girls, the claim that students at Cornell had extra-sensory perception, the claim that women were three times more likely to wear red or pink clothing during certain times of the month, the claim that single women were 20 percentage points more likely to support Barack Obama during certain times of the month, and the claim that political moderates perceived the shades of gray more accurately than extremists on the left and right”
Is there even an attempt some overarching theoretical importance here, or in most social science? Say what you want about the limitations of utility theory in economics, it’s at least a theory of some range.
Does this effect hold only for US state governors or does it apply to any popularly elected office like legislator, mayor, dogcatcher, or senior class president?
Good question. We are unable to look into this in our study, but do check out this study: https://doi.org/10.1016/j.jebo.2019.09.003
“If an estimate of 5-10 years is two or three standard errors away from zero, than an effect of 1 year, or even 2 years, is statistically undetectable. So the study is really set up only to catch artifacts or noise.”
This is the key point. I checked the paper as published, and there is no discussion at all of the magnitudes of the standard errors. They are reported in Table 1 but the only thing that’s said is how they are calculated. The SEs are about 2-3 years. If the authors had discussed the SEs they would have had to confront the noisiness of the estimates directly, and the conclusions would (I hope) have been more cautious.
Very interesting and educational dissection of an analysis.
The link between success and longevity is discussed in detail
in Michael Marmot’s “Status Syndrome”. I remember he mentioned a study which
compared longevity of leading actors who won an Oscar vs leading actors who didn’t.
The study concluded the Oscar winning actors lived longer.
I’m now wondering how large was their sample and how big the effect.
Maxim:
Here’s an example from the early days of this blog.
Long-time reader, first comment. Thanks for all the interesting information on your blog.
My question about this study, a priori, is why is it worth doing at all? Take the conclusion of the paper at face value – who cares? People considering running for governor? I suppose there is always knowledge for knowledge’s sake, but then we could look at nearly any pair of variables.
I was able to read the abstract, but it didn’t really say why anyone would be interested in the answer.
Mweiner:
People can differ as to how interesting they find this claim. As Larsen says, there is already a literature on this topic, so there are some people who are interested in it. As for me, I’m interested in the example more for the larger methodological issues that it raises.
“there’s an attitude that causal identification + statistical significance = discovery, or that causal identification + robust statistical significance = discovery”
Can someone explain what the causal identification here is? Is losing a close election assumed to be a random event?
It’s my understanding that RDD can be performed without causal identification (i.e. there could still be confounders unaccounted for).
A clear indication that there’s no causal relationship between the two (or at least that there’s some unobserved confounder) is that same candidate who won and lost two different races have the same life span.
There are several candidates in the dataset that have won=0 and won=1. These cannot be treated as independent observations.
Michael:
The causal identification is that whether you get just over 50% of the vote or just under 50% of the vote is essentially a random outcome.
The causal identification in this example is much stronger than the causal identification in that notorious air-pollution-in-China example, as there they are comparing cities that are north or south of a particular river. Whether a city is north or south of a river is not randomly assigned in any way.
“…losing a close election causes U.S. governors to die 5-10 years longer”
That sounds like a horrible deathbed.
This is a really terrific series of posts. You have complicated thoughts and you’ve hit a sweet spot where the ordering is consistent across the meanings so your general impetus can be inferred across the post(s). Conveying in depth is hard. Thanks.
It strikes me how much of the work is uncovering implicit errors in thought as they translate into design. Like product testing where the product is not defined but it can be measured. It betrays its true identiy in identifiable, quantifiable ways.
Here’s something I hope is entertaining: you know how we are taught that people thought witches would float? They’d take a woman accused of witchcraft, and they’d test to see if she’d float (when tossed in with her arms bound). Really stupid people back then: if she drowns, then she’s not a witch, so the test is stupid. Doesnt identify witches. Kills innocent women. But what if that is wrong? Because the point was to drown the women to find a witch. They werent looking to identify the innocent. They were hoping to find a witch. Or with exclamation point: a witch! A real honest-to-God witch! Now one can argue they didnt find one because they didnt drown enough women! Their sample size was insufficient to identity an effect. If all you need is one witch, why not keep drowning them … and then it becomes a fairytale or religious myth.
But wait! There’s more! If you toss a woman in with arms bound, she’ll kick until exhausted … and it certainly looks like she’s floating until she sinks. And then maybe she’ll come back up because you’ve heard it can be like that with witches. That would turn it into Monty Python sketch: I think she’s a witch! She’s floating! No, she’s just bobbing up to gulp air. (On the TV show, it would be part of the news, and now to Sheffington-on-Dorking where the annual witch survey is being conducted.)
As a robustness check, I was curious what you’d see with cutoffs besides 0. Zero makes the most intuitive sense as a cutoff since it has real-world consequences, but if the life span effect is due to those consequences, then I’d expect the effect to be stronger at that cutoff than others. It doesn’t seem to be.
https://github.com/jonspring/discontinuity/blob/master/fileb23c55435f90.gif
code: https://github.com/jonspring/discontinuity
That’s an interesting approach! We did consider the relevance of alternative cutoffs. When we estimated the main results with synthetic cutoffs, we found no significant effects (these results are available in appendix 3.6).
Thanks for doing that, I think this is a great illustration of the fact (if it is a fact) that you can’t trust regression discontinuity analysis for this sort of thing. In fact, the discontinuity is nearly never zero and for many vote margins it is substantially larger than for a vote margin very close to zero! I suppose someone can make up a Just So Story for why losing by 5 percentage points should make you live a lot longer but losing by 1 will shorten your life, or whatever (I’ve already forgotten what the plots show) but honestly this just looks like noise-fitting, which is what I think it is.
One can imagine that losing a close election (by 1 percentage point) is more stressful and traumatic than clearly losing.
I’m surprised no one has discussed the priors here. There seems to be an assumption that the causal arrow runs from election results to lifespan, but my prior is that it is as likely to be the other way around. Candidates who subsequently live longer (controlling for age) are likely to have personal attributes that contribute to this outcome. They may be healthier and more energetic. They may be wealthier. They may be more socially connected. In other words, there may be a “healthy politician effect” analogous to the “healthy worker effect”.
These attributes would presumably affect the likelihood of winning an election *if and only if the election were competitive*, which would explain why we might see different slopes in the neighborhood of the 0-vote difference line.
This is all very iffy, and I’m not sure whether it alters the prior expectation of the study finding, but it definitely alters the interpretation.
It’s just a variant of the old “correlation is not causality” thing — e.g., Shoe size predicts reading exam score for children.
Peter, Martha:
This one’s a bit different, though, because it seems reasonable to consider the intermediate outcome—whether the election result is just above 50% or just below—to be the equivalent of randomly assigned. Really, though, the model has lots of problems as can be seen by its implications of life expectancies for candidates who just win a close election, win by 5%, etc. It’s the usual story of overfitting patterns in observational data.
” I do not believe that losing a close election causes U.S. governors to die 5-10 years longer” is slightly broken. Maybe ” I do not believe that losing a close election causes U.S. governors to die 5-10 years sooner”?
Andrew, the link to your response to Erik’s response, is the same as the link to Erik’s response. Do you have another response somewhere?
Link fixed; thanks.
Wow. I agree with this:
“1. Common sense”
The math is excellent but hardly necessary. There are so many ways this can be shown to be stupid it’s hard to count them.
1) if someone has lost a close election and has cancer, there is no medicine to counteract it then? What specifically is the medical effect?
2) what other life events are playing havoc with our longevity? What about:
getting fired
getting cheated on by a spouse
having an immediate family member murdered
being a victim of sexual or other assault
3a) we already know longevity has a genetic component. So how does losing an election interact with one’s genes? Does it overpower nature? Perhaps the next study should compare gubernatorial life span with gubernatorial parent life span. Is the regression discontinuity retroactive?
3b) continuing with genetics: perhaps it works the other way around: if my family has a history of short lifespan, am I more likely to loose a close election? Or if my family is long-lived should I run for office?
This kind of study makes alchemy look like science.
So I really appreciate the thoroughness of this post.
I am about to embark on pre-registering an RDD that’s going to be relevant to an upcoming policy change in education policy in my state. I have done the power analysis and I know that I am really only able to detect effect sizes that are around 0.3. All of the meta-analyses are suggestive that I will be grossly underpowered to find the effect size that existing literature ~0.06. It’s a relevant and ongoing policy question but I know this individual estimate is likely to be noise. How can I make my work as transparent and as useful for all the folks who might want to include my findings in a subsequent metanalysis.
“How can I make my work as transparent and as useful for all the folks who might want to include my findings in a subsequent metanalysis.”
1) Get excellent data.
2) Compile and store data in a relational database with proper data validation.
3) develop additional tests beyond database validation to look for invalid data.
4) if data acquisition is ongoing, run the data tests frequently to catch any problems quickly.
Kevin Chen also provides some interesting points on Twitter (focusing on different procedures): https://twitter.com/jiafengchen42/status/1278896348650065927
I must confess that when I see results like this I always wonder if the authors really believe them–I mean believe them enough to put money on it. I’d be more than happy to bet a substantial amount of money that if you developed a similar dataset for U.S House of Representative races or Senate races and did the same analysis, you wouldn’t see an effect size of 5 or more years. And I don’t see any reason why the psychological effects of losing these races would be drastically different than losing a race for governor.
That’s fair. Yes, I believe in the study and, sure, why not put money on the central finding… Also, if the odds are very good I would even be willing to bet on studies I don’t necessarily believe in.
For the specific suggestion, there is already another study looking into these elections. I mention it in my response and you can find it here: https://doi.org/10.1016/j.jebo.2019.09.003.
For a study on prediction markets in relation to replications, see this in PNAS (of all places): https://www.pnas.org/content/112/50/15343
I’m cross-posting from PSR, so I’ll stay anonymous, but there’s a real missing substantive element here no one is picking up on and that’s a selection effect. Put simply, in a close race, fewer voters with weaker preferences for either candidate are making the decision. And the health of the candidate may very well play into it. It could be something as simple as age, but it could also be being in or out of shape.
It could also be that healthier candidates are more able to engage in the sort of retail politics that wins close elections.
Years ago, there were studies that showed that winning an Oscar made you live longer, until some scholars factored in the inherent bias of the academy toward healthier actors. https://projecteuclid.org/download/pdfview_1/euclid.aoas/1310562204
The replication data (as far as I can tell) cannot balance on the health history and appearance of individual candidates. So, to me, this finding is just an artifact of the Healthy Performer Survivor Bias in US Governor’s races.
Anon:
This could be, but I think the key point is my item 4 above. These data are so noisy, and any realistic effect size will be so small, that all these analyses are just sifting through noise.
Andrew, thanks for the analysis. Out of curiosity, I fit a simple linear regression in R using your cleaned dataset (more_years ~ age). I converted “won” to an indicator variable and added it into a 2nd model (more_years ~ age + won). I also didn’t use win/loss margin as a subset at all and the adjusted R^2 was nearly identical between both, indicating that the result of an election would have no additional predictive power on life expectancy over age alone.
My thought process is if winning or losing an election does not have an impact on longevity, then the magnitude of the win or loss would also not have explanatory power.
anon, just to confirm: we do not have any data on the health history and appearance of the individual candidates. This data would indeed be interesting to look at to rule out potential self-selection effects.
Borgschulte and Vogler (2019, https://doi.org/10.1016/j.jebo.2019.09.003) also find a positive effect of winning office on longevity (relying on 20,257 observations and, accordingly, deal with less noise than our study). I am mentioning this study here as they provide a similar point in footnote 20 (i.e. the relevance of including health-related measures): “An analysis of observed pre-election health-related measures such as the height and weight of candidates, would be valuable in this setting. Unfortunately, such data to our best knowledge is unavailable for the vast majority of candidates.”
OK, I think I finally understand Andrew’s problem with RDD:
If the forcing variable is only weakly associated with the observed outcome variable, then there will be large residual variance. If, moreover, the average treatment effect at the cutoff is small, then any estimate of it will be extremely noisy. In particular, conditional on statistical significance, there is a high probability that the sign of the estimate will be wrong (‘type S error’), and the magnitude of the estimate will on average be excessively large (‘type M error’). Because of this, even if we have good reason to be interested in the average treatment effect at the cutoff, and even if we believe the semi-continuity assumption holds (at least approximately), we don’t really learn anything from a significant RDD estimate of said effect.
Furthermore, since the typical estimator involves fitting separate curves to either side of the cutoff, and comparing their predictions at the threshold, this makes the estimate even noisier because we’re taking a difference of two extrapolative predictions. This problem is made even worse if our curve fitting models have bad extrapolative properties (e.g., high degree polynomials), but remains even if we use methods with linear extrapolation (e.g., LOESS).
Finally, there is the cultural observation that if we think RDD + statistical significance = profit, we will not pay sufficient attention to whether the forcing variable is strongly related to the observed outcome, whether the average treatment effect at the cutoff is plausibly large, and whether the extrapolative behavior of our curve fitting model is good.
Some analytic correctives include controlling for important (pre-treatment) predictors of the observed outcome to reduce residual variance, and fitting a model that estimates the discontinuity in a way that is interpolative rather than extrapolative (e.g., Daniel Lakeland’s sigmoid smoothing device).
Did I pass this ideological Turing Test? All of this makes good sense to me, I’ve just never seen you lay the full set of considerations out in this way.
What I’m less clear about is what forking paths has to do with this, given that there are pretty standard workflows researchers in this area tend to use. Once you’ve chosen a treatment to study, the forcing variable and the cutoff are already given. The only researcher degree of freedom is choice of outcome, and this is a problem with any study that isn’t pre-registered, not just RDD.
I’m also unclear about why you always talk about observation studies needing to start with the comparison of group means, followed by adjusting for differences between groups. I understand that controlling for (pre-treatment) predictors can reduce residual variance, and so limit type M and type S errors, but if we stipulate semi-continuity there isn’t any issue of confounding by these variables. One of the appeals of this identification strategy is that it doesn’t require us to measure every confounder and correctly specify it in our regression adjustments. Why do you say we need to control for differences between groups?
Anyway, if I’ve at least (mostly) characterized your views correctly this will be very clarifying for me, and hopefully for anyone else similarly lost in trying to understand your perspective here.
This is a pretty good summary.
Glad to hear you think so.
There was an old thread on EJMR about a prior RDD post from this blog, and the reception was quite negative. In particular, there seemed to be confusion about how the forcing variable could possibly be an unimportant variable to control for, when in the context of a sharp RDD it is the sole determinant of treatment assignment. If I (now) understand Andrew correctly, the importance he’s concerned with is importance for predicting the observed outcome, not the treatment assignment. If the forcing variable is unimportant in this sense, we will have large residual variance, and the design will accordingly suffer from large type S and type M errors.
I suspect applied microeconomists would be much more sympathetic to Andrew’s concerns (as I’ve characterized them) if they appreciated this distinction, which I have to admit took me some time after reading many posts on this blog.
EJMR is transparently careerism over truth
Not endorsing EJMR. Just noting that someone posted there saying Andrew doesn’t seem to realize that the forcing variable is the only important variable since it fully determines the treatment assignment, and that post got a large number of upvotes and no downvotes. If that’s indicative, it means they think Andrew’s comments here and elsewhere come from him not understanding how RDD works, when in fact Andrew is making a very valid point they should be reflecting on. They won’t, though, unless this confusion about what Andrew is saying is cleared up, which I hope my summary post semi-accomplished.
Here is my quick take on the data.
http://models.street-artists.org/2020/07/05/regression-discontinuity-fails-again/
Using LOESS with different bandwidths, we can investigate assumptions of smoothness vs of rapid changes near 0. I plot 3 LOESS curves with 0.2 0.1 and 0.05 bandwidth (this bandwidth is fraction of the data points to be used in a given fit).
Bandwidths of 0.2 mean we are assuming the function is smooth and slowly changing, so that the overall behavior through a given region is best estimated by smoothing through that large region. A bandwidth of 0.05 means we accept that only the closest 5% of the data is relevant to the question of the behavior of the function at any given point.
If there is a step-like change in the expected value near x=0 then the smaller bandwidth LOESS fits will tend to jump upwards as they transition across the x=0 boundary.
In fact, given the noise in the data if you chose any two points on the loess curve that are apart by say 1 point in margin_pct_1 you will see a difference in lifespan that is randomly fluctuating wildly in the region of x=0
The claimed effect size also happens to be the grid-size here… 5 years. The entire function can be approximated by y = 23 + normal(0,2.5) around x=0 or so. There is nowhere on these functions where you can get a jump of 5 to 10 years without cherry picking out two peaks.
So if Erik is correct, it means that the whole of the effect is canceled out precisely by the covariates he adjusts for for these individuals. Since the people winning the elections didn’t actually live longer, they must have been much much sicker than the people they were running against, and if they hadn’t won the election they’d have died 5 to 10 years earlier than they did. Good thing they won and extended their life just exactly to the average.
:-(
Thanks for the loess plots and discussion.
Ram:
I’ve been thinking of writing yet another post on this, but it’s so exhausting sometimes. Anyway, here’s the story, which I can put here as a placeholder for now:
1. Given the data available, the variability of any estimate will be huge compared to any realistic effect size, which means that you’re trying to use a bathroom scale to weigh a feather—and the feather is resting loosely in the pouch of a kangaroo that is vigorously jumping up and down. This is my point #4 in the above post. The study never had a chance.
2. The above point arises whether you’re doing regression discontinuity, instrumental variables, or just plain regression. It would even come up if you were doing a randomized controlled trial. To do causal inference, you need identification and you need precision. In this case, you don’t got the precision, and that’s the case whether or not you have identification.
3. All the details of the discontinuity analysis are a distraction—but they can be useful in that they can help us understand what went wrong. In particular, the third and fourth graphs above show a characteristic pattern that we often see when regression discontinuity analyses go wrong: the fitted curve shows an artifactual discontinuity that is there to counteract an artifactual local negative slope.
4. What’s the biggest problem with regression discontinuity? In addition to the false sense of security that it gives to researchers (similar to the problem that comes from trust in statistically significant estimates that come from randomized experiments), the big problem with regression discontinuity is that researchers are encouraged to forget about all the other background variables in the problem. Just because the treatment assignment is determined only from a particular variable X, that doesn’t mean that you can’t use other predictors in your regression. It’s an observational study, and you want to adjust for differences between the treatment and control groups. It’s naive and silly to think that this one X variable will capture all the differences.
5. So why talk about forking paths? Forking paths don’t come up in the four items above. The reason why I talk about forking paths is that this helps us understand how it is that researchers can come up with statistically significant results from data where the noise overwhelms the signal. We talk about forking paths to resolve the cognitive dissonance that otherwise arises from the apparent strength of the published evidence. To put it another way: the top graph in the above post, reproduced from the published article, looks pretty impressive. Forking paths helps us understand how this happens. I purposely use the term “forking paths” rather than “p-hacking” so as not to imply that there was intentional sorting of results.
5. You ask why I recommend first comparing group means and then adding adjustments from there. I recommend this because it helps me better understand what the statistical analysis is doing. In this case, none of it really matters given point 1 above, but for analyses with a higher signal-to-noise ratio I think it’s important to understand what the statistical adjustments are doing.
6. Finally, I find it super-frustrating that people can read these critiques and still think the original studies are OK. I think that some of this is a lack of understanding of subtle statistical concepts, some of it is rule-following, and some of it is people taking sides. In any case, it’s frustrating!
Thanks for responding at length, Andrew. This clarifies a lot.
I think we’re in complete agreement about 1-3. On 4, I agree that ignoring other variables is a mistake, though I continue to think the mistake consists in not parsing out more of the residual variance, rather than adjusting for differences between the groups, since if the identification strategy is compelling the latter shouldn’t matter so much. By contrast, the former matters either way because it also helps with the signal-to-noise issue you’re raising. Both of your 5s make more sense now. And on 6, I agree. As I mentioned in an earlier comment, when I see these papers I have the same instinctive reaction as you, and find it odd that people buy these results despite their manifest implausibility. And yet I’ve had difficulty pinpointing where these papers are going awry. I think your diagnoses are basically correct as to what’s going wrong, it’s just taken a few rounds of this for me to correctly understand them. And I worry many of the people who actually employ this design in their work have the same confusions about your analysis that I did, which might be why they continue to disregard it.
Andrew,
1-3. I fully agree that precision is crucial. We also agree that we find a huge effect in our study. Again, we would love to have a lot more data. We don’t find much variability in these estimates and it’s similar to what is reported in Borgschulte and Vogler (2019). Accordingly, based upon previous research, our discussion and the tests we provide, my best guess is that the LATE is closer to 5 years than 0 years, but definitely also closer to 5 years than 10 years. You find all of these numbers meaningless here as it’s basically all noise (and no signal). I still believe that there is something useful here. I can understand you find this frustrating given your view on our study (that it never had a chance) and your views on RDD more generally. Again, I am not saying our study is perfect or conclusive (it’s not conclusive and definitely not perfect). The comments above have been very constructive and useful — and I believe that something can be gained from our study.
4. Yes. That’s also the reason we include covariates in our analysis (both state and candidate covariates) and report the results with and without covariates. I also agree that “an attitude that causal identification + statistical significance = discovery” is problematic — and we can learn a lot more about what can be gained from an RDD estimate by treating it as an observational study rather than an experiment (or “natural experiment”).
5. I agree. Group means are informative and a good starting point.
6. I don’t see anybody picking sides — and as I wrote in my response: “this is not about being on one side or the other”. I do find your language confrontational at times that might force some people to ‘pick a side’ (agree that our study is a scientific failure or a great success). However, I see most people engaging in a healthy discussion without saying that everything’s OK.
Dude, nothing personal but in ascribing anything meaningful to this data in terms the effect you’re seeking, you’re grasping at straws. You should see that form the get-go. The distribution of the raw data is random. There’s not even the slightest hint of a pattern, yet you propose to extract a massive causal effect from it. If this effect is so large and prominent, why isn’t it visible in the raw data?
I mean dude if I tried to publish data like that for some chemical and claim an effect on life expectancy, even the EPA would cringe. There’s no effect. There’s nothing in your data. Yet you persist in defending it. Just withdraw it. Issue a mea culpa, learn from it and move on.
There’s every reason Andrew’s language should be ‘confrontational at times’: you’re a professional scientists and this research has fatal and blatant flaws. Work like this erodes the integrity of science. You’re a grown-up, not a child who’s self-esteem needs care and nurture. You can handle it.
jim,
Thanks for the comment. No worries, I can handle it. However, I’m not sure the confrontational tone is needed to convey what you think of the data, study and findings. It’s totally fair that you believe that the approach we pursue in our study is “stupid” in so many “it’s hard to count them”, and I simply disagree. I have nothing to add that I haven’t already said in my comments above and in my response (including why I don’t believe we can assess the LATE by looking at the raw data).
Erik:
My language is confrontational only in the sense that I don’t think this study adds anything to our understanding, except to the extent that it helps us build understanding as to how people can fool themselves using regression discontinuity analyses. But I agree that the discussion here has been productive. When I was speaking of people taking sides, I was not talking about your post (I criticized your study, it’s completely legitimate, not “taking sides” at all, for you to defend it!) or the comments here; I was talking about forums such as EJMR and twitter which seem more focused on zingers, soundbites, and statements of allegiance rather than on thoughtful commentary and responses.
Going off on a different tack, and regarding Erik’s comment that Andrew’s code is R that would have been written in the 1990s rather than now, are there any pointers to how R style for this sort of problem has changed in the time period? I find it a bit surprising that the style one should use for something as fundamental as regression analysis should have changed hugely, but that may simply indicate how bad I have been at keeping up with the evolution of good R style.
Thanks
It was a random observation that I should not have included in my blog post. It’s a matter of personal preference. Personally, I aim to comply with the principles outlined in the tidyverse style guide: https://style.tidyverse.org/
Thanks for the reference.