A few months ago I sent the following message to some people:
Dear philosophically-inclined colleagues:
I’d like to organize an online discussion of Deborah Mayo’s new book.
The table of contents and some of the book are here at Google books, also in the attached pdf and in this post by Mayo.
I think that many, if not all, of Mayo’s points in her Excursion 4 are answered by my article with Hennig here.
What I was thinking for this discussion is that if you’re interested you can write something, either a review of Mayo’s book (if you happen to have a copy of it) or a review of the posted material, or just your general thoughts on the topic of statistical inference as severe testing.
I’m hoping to get this all done this month, because it’s all informal and what’s the point of dragging it out, right? So if you’d be interested in writing something on this that you’d be willing to share with the world, please let me know. It should be fun, I hope!
I did this in consultation with Deborah Mayo, and I just sent this email to a few people (so if you were not included, please don’t feel left out! You have a chance to participate right now!), because our goal here was to get the discussion going. The idea was to get some reviews, and this could spark a longer discussion here in the comments section.
And, indeed, we received several responses. And I’ll also point you to my paper with Shalizi on the philosophy of Bayesian statistics, with discussions by Mark Andrews and Thom Baguley, Denny Borsboom and Brian Haig, John Kruschke, Deborah Mayo, Stephen Senn, and Richard D. Morey, Jan-Willem Romeijn and Jeffrey N. Rouder.
Also relevant is this summary by Mayo of some examples from her book.
And now on to the reviews.
Brian Haig
I’ll start with psychology researcher Brian Haig, because he’s a strong supporter of Mayo’s message and his review also serves as an introduction and summary of her ideas. The review itself is a few pages long, so I will quote from it, interspersing some of my own reaction:
Deborah Mayo’s ground-breaking book, Error and the growth of statistical knowledge (1996) . . . presented the first extensive formulation of her error-statistical perspective on statistical inference. Its novelty lay in the fact that it employed ideas in statistical science to shed light on philosophical problems to do with evidence and inference.
By contrast, Mayo’s just-published book, Statistical inference as severe testing (SIST) (2018), focuses on problems arising from statistical practice (“the statistics wars”), but endeavors to solve them by probing their foundations from the vantage points of philosophy of science, and philosophy of statistics. The “statistics wars” to which Mayo refers concern fundamental debates about the nature and foundations of statistical inference. These wars are longstanding and recurring. Today, they fuel the ongoing concern many sciences have with replication failures, questionable research practices, and the demand for an improvement of research integrity. . . .
For decades, numerous calls have been made for replacing tests of statistical significance with alternative statistical methods. The new statistics, a package deal comprising effect sizes, confidence intervals, and meta-analysis, is one reform movement that has been heavily promoted in psychological circles (Cumming, 2012; 2014) as a much needed successor to null hypothesis significance testing (NHST) . . .
The new statisticians recommend replacing NHST with their favored statistical methods by asserting that it has several major flaws. Prominent among them are the familiar claims that NHST encourages dichotomous thinking, and that it comprises an indefensible amalgam of the Fisherian and Neyman-Pearson schools of thought. However, neither of these features applies to the error-statistical understanding of NHST. . . .
There is a double irony in the fact that the new statisticians criticize NHST for encouraging simplistic dichotomous thinking: As already noted, such thinking is straightforwardly avoided by employing tests of statistical significance properly, whether or not one adopts the error-statistical perspective. For another, the adoption of standard frequentist confidence intervals in place of NHST forces the new statisticians to engage in dichotomous thinking of another kind: A parameter estimate is either inside, or outside, its confidence interval.
At this point I’d like to interrupt and say that a confidence or interval (or simply an estimate with standard error) can be used to give a sense of inferential uncertainty. There is no reason for dichotomous thinking when confidence intervals, or uncertainty intervals, or standard errors, are used in practice.
Here’s a very simple example from my book with Jennifer:
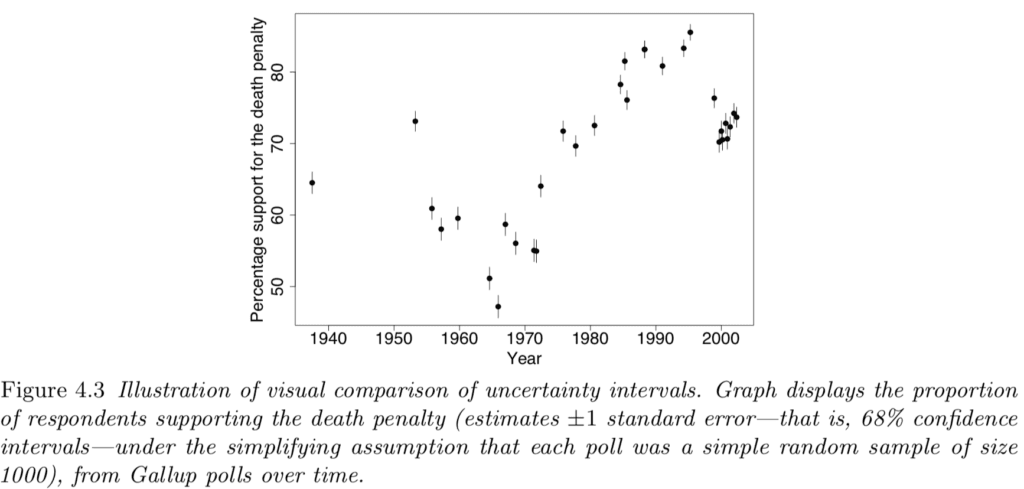
This graph has a bunch of estimates +/- standard errors, that is, 68% confidence intervals, with no dichotomous thinking in sight. In contrast, testing some hypothesis of no change over time, or no change during some period of time, would make no substantive sense and would just be an invitation to add noise to our interpretation of these data.
OK, to continue with Haig’s review:
Error-statisticians have good reason for claiming that their reinterpretation of frequentist confidence intervals is superior to the standard view. The standard account of confidence intervals adopted by the new statisticians prespecifies a single confidence interval (a strong preference for 0.95 in their case). . . . By contrast, the error-statistician draws inferences about each of the obtained values according to whether they are warranted, or not, at different severity levels, thus leading to a series of confidence intervals. Crucially, the different values will not have the same probative force. . . . Details on the error-statistical conception of confidence intervals can be found in SIST (pp. 189-201), as well as Mayo and Spanos (2011) and Spanos (2014). . . .
SIST makes clear that, with its error-statistical perspective, statistical inference can be employed to deal with both estimation and hypothesis testing problems. It also endorses the view that providing explanations of things is an important part of science.
Another interruption from me . . . I just want to plug my paper with Guido Imbens, Why ask why? Forward causal inference and reverse causal questions, in which we argue that Why questions can be interpreted as model checks, or, one might say, hypothesis tests—but tests of hypotheses of interest, not of straw-man null hypotheses. Perhaps there’s some connection between Mayo’s ideas and those of Guido and me on this point.
Haig continues with a discussion of Bayesian methods, including those of my collaborators and myself:
One particularly important modern variant of Bayesian thinking, which receives attention in SIST, is the falsificationist Bayesianism of . . . Gelman and Shalizi (2013). Interestingly, Gelman regards his Bayesian philosophy as essentially error-statistical in nature – an intriguing claim, given the anti-Bayesian preferences of both Mayo and Gelman’s co-author, Cosma Shalizi. . . . Gelman acknowledges that his falsificationist Bayesian philosophy is underdeveloped, so it will be interesting to see how its further development relates to Mayo’s error-statistical perspective. It will also be interesting to see if Bayesian thinkers in psychology engage with Gelman’s brand of Bayesian thinking. Despite the appearance of his work in a prominent psychology journal, they have yet to do so. . . .
Hey, not quite! I’ve done a lot of collaboration with psychologists; see here and search on “Iven Van Mechelen” and “Francis Tuerlinckx”—but, sure, I recognize that our Bayesian methods, while mainstream in various fields including ecology and political science, are not yet widely used in psychology.
Haig concludes:
From a sympathetic, but critical, reading of Popper, Mayo endorses his strategy of developing scientific knowledge by identifying and correcting errors through strong tests of scientific claims. . . . A heartening attitude that comes through in SIST is the firm belief that a philosophy of statistics is an important part of statistical thinking. This contrasts markedly with much of statistical theory, and most of statistical practice. Given that statisticians operate with an implicit philosophy, whether they know it or not, it is better that they avail themselves of an explicitly thought-out philosophy that serves practice in useful ways.
I agree, very much.
To paraphrase Bill James, the alternative to good philosophy is not “no philosophy,” it’s “bad philosophy.” I’ve spent too much time seeing Bayesians avoid checking their models out of a philosophical conviction that subjective priors cannot be empirically questioned, and too much time seeing non-Bayesians produce ridiculous estimates that could have been avoided by using available outside information. There’s nothing so practical as good practice, but good philosophy can facilitate both the development and acceptance of better methods.
E. J. Wagenmakers
I’ll follow up with a very short review, or, should I say, reaction-in-place-of-a-review, from psychometrician E. J. Wagenmakers:
I cannot comment on the contents of this book, because doing so would require me to read it, and extensive prior knowledge suggests that I will violently disagree with almost every claim that is being made. In my opinion, the only long-term hope for vague concepts such as the “severity” of a test is to embed them within a rational (i.e., Bayesian) framework, but I suspect that this is not the route that the author wishes to pursue. Perhaps this book is comforting to those who have neither the time nor the desire to learn Bayesian inference, in a similar way that homeopathy provides comfort to patients with a serious medical condition.
You don’t have to agree with E. J. to appreciate his honesty!
Art Owen
Coming from a different perspective is theoretical statistician Art Owen, whose review has some mathematical formulas—nothing too complicated, but not so easy to display in html, so I’ll just link to the pdf and share some excerpts:
There is an emphasis throughout on the importance of severe testing. It has long been known that a test that fails to reject H0 is not very conclusive if it had low power to reject H0. So I wondered whether there was anything more to the severity idea than that. After some searching I found on page 343 a description of how the severity idea differs from the power notion. . . .
I think that it might be useful in explaining a failure to reject H0 as the sample size being too small. . . . it is extremely hard to measure power post hoc because there is too much uncertainty about the effect size. Then, even if you want it, you probably cannot reliably get it. I think severity is likely to be in the same boat. . . .
I believe that the statistical problem from incentives is more severe than choice between Bayesian and frequentist methods or problems with people not learning how to use either kind of method properly. . . . We usually teach and do research assuming a scientific loss function that rewards being right. . . . In practice many people using statistics are advocates. . . . The loss function strongly informs their analysis, be it Bayesian or frequentist. The scientist and advocate both want to minimize their expected loss. They are led to different methods. . . .
I appreciate Owen’s efforts to link Mayo’s words to the equations that we would ultimately need to implement, or evaluate, her ideas in statistics.
Robert Cousins
Physicist Robert Cousins did not have the time to write a comment on Mayo’s book, but he did point us to this monograph he wrote on the foundations of statistics, which has lots of interesting stuff but is unfortunately a bit out of date when it comes to the philosophy of Bayesian statistics, which he ties in with subjective probability. (For a corrective, see my aforementioned article with Hennig.)
In his email to me, Cousins also addressed issues of statistical and practical significance:
Our [particle physicists’] problems and the way we approach them are quite different from some other fields of science, especially social science. As one example, I think I recall reading that you do not mind adding a parameter to your model, whereas adding (certain) parameters to our models means adding a new force of nature (!) and a Nobel Prize if true. As another example, a number of statistics papers talk about how silly it is to claim a 10^{⁻4} departure from 0.5 for a binomial parameter (ESP examples, etc), using it as a classic example of the difference between nominal (probably mismeasured) statistical significance and practical significance. In contrast, when I was a grad student, a famous experiment in our field measured a 10^{⁻4} departure from 0.5 with an uncertainty of 10% of itself, i.e., with an uncertainty of 10^{⁻5}. (Yes, the order or 10^10 Bernoulli trials—counting electrons being scattered left or right.) This led quickly to a Nobel Prize for Steven Weinberg et al., whose model (now “Standard”) had predicted the effect.
I replied:
This interests me in part because I am a former physicist myself. I have done work in physics and in statistics, and I think the principles of statistics that I have applied to social science, also apply to physical sciences. Regarding the discussion of Bem’s experiment, what I said was not that an effect of 0.0001 is unimportant, but rather that if you were to really believe Bem’s claims, there could be effects of +0.0001 in some settings, -0.002 in others, etc. If this is interesting, fine: I’m not a psychologist. One of the key mistakes of Bem and others like him is to suppose that, even if they happen to have discovered an effect in some scenario, there is no reason to suppose this represents some sort of universal truth. Humans differ from each other in a way that elementary particles to not.
And Cousins replied:
Indeed in the binomial experiment I mentioned, controlling unknown systematic effects to the level of 10^{-5}, so that what they were measuring (a constant of nature called the Weinberg angle, now called the weak mixing angle) was what they intended to measure, was a heroic effort by the experimentalists.
Stan Young
Stan Young, a statistician who’s worked in the pharmaceutical industry, wrote:
I’ve been reading at the Mayo book and also pestering where I think poor statistical practice is going on. Usually the poor practice is by non-professionals and usually it is not intentionally malicious however self-serving. But I think it naive to think that education is all that is needed. Or some grand agreement among professional statisticians will end the problems.
There are science crooks and statistical crooks and there are no cops, or very few.
That is a long way of saying, this problem is not going to be solved in 30 days, or by one paper, or even by one book or by three books! (I’ve read all three.)
I think a more open-ended and longer dialog would be more useful with at least some attention to willful and intentional misuse of statistics.
Chambers C. The Seven Deadly Sins of Psychology. New Jersey: Princeton University Press, 2017.
Harris R. Rigor mortis: how sloppy science creates worthless cures, crushes hope, and wastes billions. New York: Basic books, 2017.
Hubbard R. Corrupt Research. London: Sage Publications, 2015.
Christian Hennig
Hennig, a statistician and my collaborator on the Beyond Subjective and Objective paper, send in two reviews of Mayo’s book.
Here are his general comments:
What I like about Deborah Mayo’s “Statistical Inference as Severe Testing”
Before I start to list what I like about “Statistical Inference as Severe Testing”. I should say that I don’t agree with everything in the book. In particular, as a constructivist I am skeptical about the use of terms like “objectivity”, “reality” and “truth” in the book, and I think that Mayo’s own approach may not be able to deliver everything that people may come to believe it could, from reading the book (although Mayo could argue that overly high expectations could be avoided by reading carefully).
So now, what do I like about it?
1) I agree with the broad concept of severity and severe testing. In order to have evidence for a claim, it has to be tested in ways that would reject the claim with high probability if it indeed were false. I also think that it makes a lot of sense to start a philosophy of statistics and a critical discussion of statistical methods and reasoning from this requirement. Furthermore, throughout the book Mayo consistently argues from this position, which makes the different “Excursions” fit well together and add up to a consistent whole.
2) I get a lot out of the discussion of the philosophical background of scientific inquiry, of induction, probabilism, falsification and corroboration, and their connection to statistical inference. I think that it makes sense to connect Popper’s philosophy to significance tests in the way Mayo does (without necessarily claiming that this is the only possible way to do it), and I think that her arguments are broadly convincing at least if I take a realist perspective of science (which as a constructivist I can do temporarily while keeping the general reservation that this is about a specific construction of reality which I wouldn’t grant absolute authority).
3) I think that Mayo does by and large a good job listing much of the criticism that has been raised in the literature against significance testing, and she deals with it well. Partly she criticises bad uses of significance testing herself by referring to the severity requirement, but she also defends a well understood use in a more general philosophical framework of testing scientific theories and claims in a piecemeal manner. I find this largely convincing, conceding that there is a lot of detail and that I may find myself in agreement with the occasional objection against the odd one of her arguments.
4) The same holds for her comprehensive discussion of Bayesian/probabilist foundations in Excursion 6. I think that she elaborates issues and inconsistencies in the current use of Bayesian reasoning very well, maybe with the odd exception.
5) I am in full agreement with Mayo’s position that when using probability modelling, it is important to be clear about the meaning of the computed probabilities. Agreement in numbers between different “camps” isn’t worth anything if the numbers mean different things. A problem with some positions that are sold as “pragmatic” these days is that often not enough care is put into interpreting what the results mean, or even deciding in advance what kind of interpretation is desired.
6) As mentioned above, I’m rather skeptical about the concept of objectivity and about an all too realist interpretation of statistical models. I think that in Excursion 4 Mayo manages to explain in a clear manner what her claims of “objectivity” actually mean, and she also appreciates more clearly than before the limits of formal models and their distance to “reality”, including some valuable thoughts on what this means for model checking and arguments from models.
So overall it was a very good experience to read her book, and I think that it is a very valuable addition to the literature on foundations of statistics.
Hennig also sent some specific discussion of one part of the book:
1 Introduction
This text discusses parts of Excursion 4 of Mayo (2018) titled “Objectivity and Auditing”. This starts with the section title “The myth of ‘The myth of objectivity'”. Mayo advertises objectivity in science as central and as achievable.
In contrast, in Gelman and Hennig (2017) we write: “We argue that the words ‘objective’ and ‘subjective’ in statistics discourse are used in a mostly unhelpful way, and we propose to replace each of them with broader collections of attributes.” I will here outline agreement and disagreement that I have with Mayo’s Excursion 4, and raise some issues that I think require more research and discussion.
2 Pushback and objectivity
The second paragraph of Excursion 4 states in bold letters: “The Key Is Getting Pushback”, and this is the major source of agreement between Mayo’s and my views (*). I call myself a constructivist, and this is about acknowledging the impact of human perception, action, and communication on our world-views, see Hennig (2010). However, it is an almost universal experience that we cannot construct our perceived reality as we wish, because we experience “pushback” from what we perceive as “the world outside”. Science is about allowing us to deal with this pushback in stable ways that are open to consensus. A major ingredient of such science is the “Correspondence (of scientific claims) to observable reality”, and in particular “Clear conditions for reproduction, testing and falsification”, listed as “Virtue 4/4(b)” in Gelman and Hennig (2017). Consequently, there is no disagreement with much of the views and arguments in Excursion 4 (and the rest of the book). I actually believe that there is no contradiction between constructivism understood in this way and Chang’s (2012) “active scientific realism” that asks for action in order to find out about “resistance from reality”, or in other words, experimenting, experiencing and learning from error.
If what is called “objectivity” in Mayo’s book were the generally agreed meaning of the term, I would probably not have a problem with it. However, there is a plethora of meanings of “objectivity” around, and on top of that the term is often used as a sales pitch by scientists in order to lend authority to findings or methods and often even to prevent them from being questioned. Philosophers understand that this is a problem but are mostly eager to claim the term anyway; I have attended conferences on philosophy of science and heard a good number of talks, some better, some worse, with messages of the kind “objectivity as understood by XYZ doesn’t work, but here is my own interpretation that fixes it”. Calling frequentist probabilities “objective” because they refer to the outside world rather than epsitemic states, and calling a Bayesian approach “objective” because priors are chosen by general principles rather than personal beliefs are in isolation also legitimate meanings of “objectivity”, but these two and Mayo’s and many others (see also the Appendix of Gelman and Hennig, 2017) differ. The use of “objectivity” in public and scientific discourse is a big muddle, and I don’t think this will change as a consequence of Mayo’s work. I prefer stating what we want to achieve more precisely using less loaded terms, which I think Mayo has achieved well not by calling her approach “objective” but rather by explaining in detail what she means by that.
3. Trust in models?
In the remainder, I will highlight some limitations of Mayo’s “objectivity” that are mainly connected to Tour IV on objectivity, model checking and whether it makes sense to say that “all models are false”. Error control is central for Mayo’s objectivity, and this relies on error probabilities derived from probability models. If we want to rely on these error probabilities, we need to trust the models, and, very appropriately, Mayo devotes Tour IV to this issue. She concedes that all models are false, but states that this is rather trivial, and what is really relevant when we use statistical models for learning from data is rather whether the models are adequate for the problem we want to solve. Furthermore, model assumptions can be tested and it is crucial to do so, which, as follows from what was stated before, does not mean to test whether they are really true but rather whether they are violated in ways that would destroy the adequacy of the model for the problem. So far I can agree. However, I see some difficulties that are not addressed in the book, and mostly not elsewhere either. Here is a list.
3.1. Adaptation of model checking to the problem of interest
As all models are false, it is not too difficult to find model assumptions that are violated but don’t matter, or at least don’t matter in most situations. The standard example would be the use of continuous distributions to approximate distributions of essentially discrete measurements. What does it mean to say that a violation of a model assumption doesn’t matter? This is not so easy to specify, and not much about this can be found in Mayo’s book or in the general literature. Surely it has to depend on what exactly the problem of interest is. A simple example would be to say that we are interested in statements about the mean of a discrete distribution, and then to show that estimation or tests of the mean are very little affected if a certain continuous approximation is used. This is reassuring, and certain other issues could be dealt with in this way, but one can ask harder questions. If we approximate a slightly skew distribution by a (unimodal) symmetric one, are we really interested in the mean, the median, or the mode, which for a symmetric distribution would be the same but for the skew distribution to be approximated would differ? Any frequentist distribution is an idealisation, so do we first need to show that it is fine to approximate a discrete non-distribution by a discrete distribution before worrying whether the discrete distribution can be approximated by a continuous one? (And how could we show that?) And so on.
3.2. Severity of model misspecification tests
Following the logic of Mayo (2018), misspecification tests need to be severe in ordert to fulfill their purpose; otherwise data could pass a misspecification test that would be of little help ruling out problematic model deviations. I’m not sure whether there are any results of this kind, be it in Mayo’s work or elsewhere. I imagine that if the alternative is parametric (for example testing independence against a standard time series model) severity can occasionally be computed easily, but for most model misspecification tests it will be a hard problem.
3.3. Identifiability issues, and ruling out models by other means than testing
Not all statistical models can be distinguished by data. For example, even with arbitrarily large amounts of data only lower bounds of the number of modes can be estimated; an assumption of unimodality can strictly not be tested (Donoho 1988). Worse, only regular but not general patterns of dependence can be distinguished from independence by data; any non-i.i.d. pattern can be explained by either dependence or non-identity of distributions, and telling these apart requires constraints on dependence and non-identity structures that can itself not be tested on the data (in the example given in 4.11 of Mayo, 2018, all tests discover specific regular alternatives to the model assumption). Given that this is so, the question arises on which grounds we can rule out irregular patterns (about the simplest and most silly one is “observations depend in such a way that every observation determines the next one to be exactly what it was observed to be”) by other means than data inspection and testing. Such models are probably useless, however if they were true, they would destroy any attempt to find “true” or even approximately true error probabilities.
3.4. Robustness against what cannot be ruled out
The above implies that certain deviations from the model assumptions cannot be ruled out, and then one can ask: How robust is the substantial conclusion that is drawn from the data against models different from the nominal one, which could not be ruled out by misspecification testing, and how robust are error probabilities? The approaches of standard robust statistics probably have something to contribute in this respect (e.g., Hampel et al., 1986), although their starting point is usually different from “what is left after misspecification testing”. This will depend, as everything, on the formulation of the “problem of interest”, which needs to be defined not only in terms of the nominal parametric model but also in terms of the other models that could not be rules out.
3.5. The effect of preliminary model checking on model-based inference
Mayo is correctly concerned about biasing effects of model selection on inference. Deciding what model to use based on misspecification tests is some kind of model selection, so it may bias inference that is made in case of passing misspecification tests. One way of stating the problem is to realise that in most cases the assumed model conditionally on having passed a misspecification test does no longer hold. I have called this the “goodness-of-fit paradox” (Hennig, 2007); the issue has been mentioned elsewhere in the literature. Mayo has argued that this is not a problem, and this is in a well defined sense true (meaning that error probabilities derived from the nominal model are not affected by conditioning on passing a misspecification test) if misspecification tests are indeed “independent of (or orthogonal to) the primary question at hand” (Mayo 2018, p. 319). The problem is that for the vast majority of misspecification tests independence/orthogonality does not hold, at least not precisely. So the actual effect of misspecification testing on model-based inference is a matter that requires to be investigated on a case-by-case basis. Some work of this kind has been done or is currently done; results are not always positive (an early example is Easterling and Anderson 1978).
4 Conclusion
The issues listed in Section 3 are in my view important and worthy of investigation. Such investigation has already been done to some extent, but there are many open problems. I believe that some of these can be solved, some are very hard, and some are impossible to solve or may lead to negative results (particularly connected to lack of identifiability). However, I don’t think that these issues invalidate Mayo’s approach and arguments; I expect at least the issues that cannot be solved to affect in one way or another any alternative approach. My case is just that methodology that is “objective” according to Mayo comes with limitations that may be incompatible with some other peoples’ ideas of what “objectivity” should mean (in which sense it is in good company though), and that the falsity of models has some more cumbersome implications than Mayo’s book could make the reader believe.
(*) There is surely a strong connection between what I call “my” view here with the collaborative position in Gelman and Hennig (2017), but as I write the present text on my own, I will refer to “my” position here and let Andrew Gelman speak for himself.
References:
Chang, H. (2012) Is Water H2O? Evidence, Realism and Pluralism. Dordrecht: Springer.Donoho, D. (1988) One-Sided Inference about Functionals of a Density. Annals of Statistics 16, 1390-1420.
Easterling, R. G. and Anderson, H.E. (1978) The effect of preliminary normality goodness of fit tests on subsequent inference. Journal of Statistical Computation and Simulation 8, 1-11.
Gelman, A. and Hennig, C. (2017) Beyond subjective and objective in statistics (with discussion). Journal of the Royal Statistical Society, Series A 180, 967–1033.
Hampel, F. R., Ronchetti, E. M., Rousseeuw, P. J. and Stahel, W. A. (1986) Robust statistics. New York: Wiley.
Hennig, C. (2010) Mathematical models and reality: a constructivist perspective. Foundations of Science 15, 29–48.
Hennig, C. (2007) Falsification of propensity models by statistical tests and the goodness-of-fit paradox. Philosophia Mathematica 15, 166-192.
Mayo, D. G. (2018) Statistical Inference as Severe Testing. Cambridge University Press.
My own reactions
I’m still struggling with the key ideas of Mayo’s book. (Struggling is a good thing here, I think!)
First off, I appreciate that Mayo takes my own philosophical perspective seriously—I’m actually thrilled to be taken seriously, after years of dealing with a professional Bayesian establishment tied to naive (as I see it) philosophies of subjective or objective probabilities, and anti-Bayesians not willing to think seriously about these issues at all—and I don’t think any of these philosophical issues are going to be resolved any time soon. I say this because I’m so aware of the big Cantor-size hole in the corner of my own philosophy of statistical learning.
In statistics—maybe in science more generally—philosophical paradoxes are sometimes resolved by technological advances. Back when I was a student I remember all sorts of agonizing over the philosophical implications of exchangeability, but now that we can routinely fit varying-intercept, varying-slope models with nested and non-nested levels and (we’ve finally realized the importance of) informative priors on hierarchical variance parameters, a lot of the philosophical problems have dissolved; they’ve become surmountable technical problems. (For example: should we consider a group of schools, or states, or hospitals, as “truly exchangeable”? If not, there’s information distinguishing them, and we can include such information as group-level predictors in our multilevel model. Problem solved.)
Rapid technological progress resolves many problems in ways that were never anticipated. (Progress creates new problems too; that’s another story.) I’m not such an expert on deep learning and related methods for inference and prediction—but, again, I think these will change our perspective on statistical philosophy in various ways.
This is all to say that any philosophical perspective is time-bound. On the other hand, I don’t think that Popper/Kuhn/Lakatos will ever be forgotten: this particular trinity of twentieth-century philosophy of science has forever left us in a different place than where we were, a hundred years ago.
To return to Mayo’s larger message: I agree with Hennig that Mayo is correct to place evaluation at the center of statistics.
I’ve thought a lot about this, in many years of teaching statistics to graduate students. In a class for first-year statistics Ph.D. students, you want to get down to the fundamentals.
What’s the most fundamental thing in statistics? Experimental design? No. You can’t really pick your design until you have some sense of how you will analyze the data. (This is the principle of the great Raymond Smullyan: To understand the past, we must first know the future.) So is data analysis the most fundamental thing? Maybe so, but what method of data analysis? Last I heard, there are many schools. Bayesian data analysis, perhaps? Not so clear; what’s the motivation for modeling everything probabilistically? Sure, it’s coherent—but so is some mental patient who thinks he’s Napoleon and acts daily according to that belief. We can back into a more fundamental, or statistical, justification of Bayesian inference and hierarchical modeling by first considering the principle of external validation of predictions, then showing (both empirically and theoretically) that a hierarchical Bayesian approach performs well based on this criterion—and then following up with the Jaynesian point that, when Bayesian inference fails to perform well, this recognition represents additional information that can and should be added to the model. All of this is the theme of the example in section 7 of BDA3—although I have the horrible feeling that students often don’t get the point, as it’s easy to get lost in all the technical details of the inference for the hyperparameters in the model.
Anyway, to continue . . . it still seems to me that the most foundational principles of statistics are frequentist. Not unbiasedness, not p-values, and not type 1 or type 2 errors, but frequency properties nevertheless. Statements about how well your procedure will perform in the future, conditional on some assumptions of stationarity and exchangeability (analogous to the assumption in physics that the laws of nature will be the same in the future as they’ve been in the past—or, if the laws of nature are changing, that they’re not changing very fast! We’re in Cantor’s corner again).
So, I want to separate the principle of frequency evaluation—the idea that frequency evaluation and criticism represents one of the three foundational principles of statistics (with the other two being mathematical modeling and the understanding of variation)—from specific statistical methods, whether they be methods that I like (Bayesian inference, estimates and standard errors, Fourier analysis, lasso, deep learning, etc.) or methods that I suspect have done more harm than good or, at the very least, have been taken too far (hypothesis tests, p-values, so-called exact tests, so-called inverse probability weighting, etc.). We can be frequentists, use mathematical models to solve problems in statistical design and data analysis, and engage in model criticism, without making decisions based on type 1 error probabilities etc.
To say it another way, bringing in the title of the book under discussion: I would not quite say that statistical inference is severe testing, but I do think that severe testing is a crucial part of statistics. I see statistics as an unstable mixture of inference conditional on a model (“normal science”) and model checking (“scientific revolution”). Severe testing is fundamental, in that prospect of revolution is a key contributor to the success of normal science. We lean on our models in large part because they have been, and will continue to be, put to the test. And we choose our statistical methods in large part because, under certain assumptions, they have good frequency properties.
And now on to Mayo’s subtitle. I don’t think her, or my, philosophical perspective will get us “beyond the statistics wars” by itself—but perhaps it will ultimately move us in this direction, if practitioners and theorists alike can move beyond naive confirmationist reasoning toward an embrace of variation and acceptance of uncertainty.
I’ll summarize by expressing agreement with Mayo’s perspective that frequency evaluation is fundamental, while disagreeing with her focus on various crude (from my perspective) ideas such as type 1 errors and p-values. When it comes to statistical philosophy, I’d rather follow Laplace, Jaynes, and Box, rather than Neyman, Wald, and Savage. Phony Bayesmania has bitten the dust.
Thanks
Let me again thank Haig, Wagenmakers, Owen, Cousins, Young, and Hennig for their discussions. I expect that Mayo will respond to these, and also to any comments that follow in this thread, once she has time to digest it all.
P.S. And here’s a review from Christian Robert.
As I might be the first commenting, I would like to thank you for organizing a reasonable number of thoughtful people to comment first and only then share.
> the most foundational principles of statistics are frequentist.
Thanks for being so clear about that and clarifying general notions of frequency evaluation.
Cantor’s corner, to me, is just a colorful restatement of fallibility in science – never any firm conclusions but rather pauses until we see good benefit/cost of something noticed to be wrong along with anticipating how it might be fixed.
> no contradiction between constructivism understood in this way and Chang’s (2012) “active scientific realism” that asks for action in order to find out about “resistance from reality”, or in other words, experimenting, experiencing and learning from error.
I believe Deborah and Chang would confirm the major source of their views on this are from CS Peirce. Sorry could not help myself and I do believe the sources of ideas are important to be aware of.
#10
Keith comment
I do always credit Peirce as the philosopher from whom I’ve learned a great deal in phil sci, and also other pragmatists. Chang may have learned something about these themes from me (he wrote a wonderful review of EGEK 20 years ago). I’d like to get your take on SIST at some point.
Interesting, didn’t realize the acceptance of the standard model was based on a free parameter like this:
https://en.wikipedia.org/wiki/Weinberg_angle
We can see how they reasoned:
Prescott, C. Y., Atwood, W. B., Cottrell, R. L. A., DeStaebler, H., Garwin, E. L., Gonidec, A., … Jentschke, W. (1978). Parity non-conservation in inelastic electron scattering. Physics Letters B, 77(3), 347–352. doi:10.1016/0370-2693(78)90722-0
So there were some models that predicted exactly A/Q^2 = 0. These are deemed inconsistent with the data: p(D|H) ~ 0 for these models. However there were also two models that allowed A/Q^2 to vary but had a free parameter to fit (the W-S model and the “hybrid” model). Due to the free parameter, predictions of these models are more vague than a point prediction.
However, we can see from their figure we see that it is not like any non-zero value for A/Q^2 would be consistent with these models. The models do predict a precise curve for a given Weinberg angle and “y” (whatever that is): https://i.ibb.co/7pRRxP4/prescott1978.png
The published more data for varying “y” and a similar chart the following year:
https://i.ibb.co/8KpxdpR/prescott1979.png
Prescott, C. Y., Atwood, W. B., Cottrell, R. L. A., DeStaebler, H., Garwin, E. L., Gonidec, A., … Jentschke, W. (1979). Further measurements of parity non-conservation in inelastic electron scattering. Physics Letters B, 84(4), 524–528. doi:10.1016/0370-2693(79)91253-x
So now we see that p(D|W-S) ~ 0.4 and p(D|”hybrid”) ~ 6e-4. They do not seem to have a prior preference between the models, so p(W-S) ~ p(“hybrid”). Remembering that we dropped other models from the denominator that were considered to have p(D|H) ~ 0:
Looks exactly like the bayesian reason that I described here:
https://statmodeling.stat.columbia.edu/2019/03/31/a-comment-about-p-values-from-art-owen-upon-reading-deborah-mayos-new-book/#comment-1009714
tl;dr:
The physicists are not just rejecting A/Q^2 = 0 and then concluding their W-S model is correct like Robert Cousins implied.
They do not consider one model in isolation, rather they compare the relative fit of a variety of possible explanations and choose the best.
Some interesting points I noticed after making the post:
1) Because both W-S and “hybrid” models have the same free parameter it doesn’t matter how vague they are when comparing the two. You can just compare the likelihoods using the single best-fit parameter for each. However, I wonder if those models that predicted a value of exactly zero got dismissed too easily.
Ie, p(D|W-S) ~ 0.4 for the “best” choice of Weinberg angle which is going to be much larger than the likelihoods from the models that predicted A/Q^2 = 0, call those collectively p(D|H). But p(D|W-S) should be lower when we consider all the possible Weinberg angles (the density is spread across all the different values), so maybe the p(D|W-S) >> p(D|H) assumption does not hold.
2) Chi-squared p-values are being used to approximate the likelihoods. Not sure if this matters. The tails will be included for all terms so will somewhat cancel out…
P-value vs likelihood (probability mass) for binomial distribution with p = 0.5: https://i.ibb.co/zJFtyYJ/Pvs-Likelihood.png
x = 0:20
likelihood = dbinom(x, 20, .5)
pval = sapply(x, function(x) binom.test(x, 20, p = 0.5)$p.value)
From this case, I would guess use of a p-value to approximate the likelihood will tend to exaggerate the support for models that are relatively accurate.
The integration of several perspectives on the book of Mayo is really nice – thank you for this initiative.
Let me share my perspective: Statistics is about information quality. If you deal with lab data, clinical trials, industrial problems or marketing data, it is always about the generation of information, and statistics should enable information quality.
In treating this issue we suggested a framework with 8 dimensions (https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2128547). My 2016 Wiley book with Galit Shmueli is about that. From this perspective you look at the generalisation of findings (the 6th information quality dimension). Establishing causality is different from a statement about association.
As pointed out, Mayo is focused on the evaluation aspects of statistics. Another domain is the way findings are presented. A suggestion I made in the past was to use alternative representations. The “trick” is to state both what you claim to have found and also what you do not claim is being supported by your study design and analysis. An explicit listing of such alternatives could be a possible requirement in research paper in a section titled “Generalisation of findings”. Some clinical researchers have already embraced this idea. An example of this form translational medicine is provided in https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3035070. Type S errors are actually speaking this language and permit to evaluate alternative representations with meaning equivalence.
So, I claim that the “statistics war” is engaged in just part of the playing ground. Other aspects, relevant to data analysis, should also be covered. For a wide angle perspective of how statistics can impact data science, beyond machine learning and algorithmic aspects, see my new book titled: The Real Work of Data Science (wiley, 2019). The challenge is to close the gap between academia and practitioners who need methods that work beyond a publication goal measured by journal impact factors.
Integration is the 3rd information quality dimensions and the collection of review in this post demonstrate, yet again, that proper integration provides enhanced information quality. This is beyond data fusion methods (An example in this area can be seen in https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3035807).
For me, the 8 information quality dimension form a comprehensive top down framework of what statistics is about, and it is beyond statistics wars…
I haven’t read the book or know anything about severity testing, but I liked Art Owen’s comment as a read in itself. Based on my own limited and brief (I’m a relative newbie) experience, the “Scientific and Advocacy Loss Functions” section of Owen’s comment really rings true. I think it might be easy to become an “advocate”, even for the most well-meaning scientist or statistician or reader of this blog, and I am skeptical that more education and better methods can ever fix this.
Also, this doesn’t contribute to discussion of Mayo’s book, but I also liked his comment on p-values in his “Abstract”. I know there’s been loads of comments on this on other posts (and I don’t wish to distract from the discussion intended), but I found his comment particularly useful from a practical as opposed to technical explanation.
“Much has been written about the misunderstandings and misinterpretations of p-values. The cumulative impact of such criticisms in statistical practice and on empirical research has been nil.”
(Berry, D. (2017), “A p-Value to Die For,” Journal of the American Statistical Association, 112, 895–897. [Taylor & Francis Online], [Web of Science ®], , [Google Scholar] , p. 896).
Garnett:
I disagree with the claim that the cumulative impact of such criticisms in statistical practice and on empirical research has been nil. For one thing, those criticisms have affected my own statistical practice and my own empirical research. For another thing, a few thousand people read my books and I think this guides practice. The claim of zero impact seems both ridiculous and without empirical support.
Andrew:
I’ll let you argue with Don Berry on that point.
I can say that your work has influenced me in many, many ways, but my opinion on all of this is inconsequential. i.e. nil.
This blog has certainly affected my statistical practice since finishing graduate school a few years ago. So, at least for me, such criticisms in statistical practice has had a profound effect.
However, as a newbie and outsider to all of this until a couple years ago, this entire topic reminds me oddly of my previous career in health and wellness with a focus on obesity prevention. One of the most difficult things in the world seems to be to change human behavior. Incentives of various sorts are always present, acknowledged or not. There seemed to be a school of thought in that arena that if you educated people enough about risks, then they would make the right choices (I guess the thinking was “logically, who wouldn’t make the right choice, considering the risks we’ve pointed out?”). Practically it didn’t seem to work or be that simple. And so, Art Owen’s comment rings particularly true.
While a claim of zero impact isn’t true (because, hey, it has already affected me, so that’s more than zero; and obviously many others), from my frame of reference, incentives are probably a large underlying piece that may not be affected by more education and better methods. So that seems worth considering.
My experience is similar and I agree completely. My goal is to understand why researchers keep doing these things despite the important and lucid criticisms. (And then, what else can we do about it?)
I plugged my own (very large and not very well written) blog post examining the severity notion in the context of adaptive trials in the comments of the previous post previewing some of Art Owen’s commentary. Here I will link to a twitter thread I recently wrote explaining the starting point of that examination. The value to readers here is that it’s a two-part thread and the first part explains (in very abbreviated fashion) what severity is (according to me, but I link Mayo’s definitive paper on the subject in the thread). Part 2 of the thread can be skipped if you don’t care about adaptive trials.
https://twitter.com/Corey_Yanofsky/status/1115725035266813953
Wow, that’s great that you finally addressed the book. I’m halfway through. I thought I’d be finished by now. Been hectic this last week.
I commend Deborah for undertaking the laudable task of presenting the history and the controversies. Very engaging work. I look forward to the discussion. As a novice, I am more cautious in drawing any generalizations.
My thinking style is some mixture of Andrew Gelman, Steven Goodman, and John Ioannidis. I am not a linear/binary thinker. One reason why I am not enamored of NHST to begin probably.
My larger focus is in widening the scope of audiences to these controversies. A hobby actually. Not a career interest as such.
To me, at the heart of statistics is not frequentism, or propositional logic, but *decision making* as such I really like Wald’s contribution. But I don’t want to focus on Wald, I want to talk about this idea of decision making:
There are basically two parts of decision making that I can think of: decision making *about our models* and decision making *about how we construe reality*. On this point, I think I’m very much with Christian Hennig’s constructivist views as I understand them (which is admittedly not necessarily that well). It’s our perception of reality that we have control over, and reality keeps smacking us when we perceive it incorrectly (as will Christian, if I perceive him incorrectly, I hope).
For me, the thing we want from science is models of how the world works which generalize sufficiently to make consistently useful predictions that can guide decisions.
We care about quantum physics for example because it lets us predict that putting together certain elements in a crystal will result in us being able to control the resistance of that crystal to electric current, or generate light of a certain color or detect light by moving charges around or stuff like that. I’m not just talking about what you might call economic utility, but also intellectual utility. Our knowledge of quantum mechanics lets people like Hawking come up with his Hawking Radiation theory, which lets us make predictions about things in the vastness of space very far from “money making”. Similarly, knowledge of say psychology can let us come up with theories about how best to communicate warnings about dangers in industrial plants, or help people have better interpersonal relationships, or learn math concepts easier, or whatever.
When it comes to decision making about our models, logic rules. If parameter equals q, then prediction in vicinity of y… If model predicts y strongly, and y isn’t happening, then parameter not close to q. That sort of thing.
Within the Bayesian formalism this is what Bayes does… it down-weights regions of parameter space that cause predictions that fail to coincide with real data. Of course, that’s only *within the formalism*. The best the formalism can do is compress our parameter space down to get our model as close as possible to the manifold where the “true” model lies. But that true model never is reachable… It’s like the denizens of flatland trying to touch the sphere as it hovers over their plane… So in this sense, the notion of propositional logic and converging to “true” can’t be the real foundation of Bayes. It’s a useful model of Bayes, and it might be true in certain circumstances (like when you’re testing a computer program you could maybe have a true value of a parameter) but it isn’t general enough. Another way to say this is “all models are wrong, but some are useful”. If all models are wrong, at least most of the time, then logical truth of propositions isn’t going to be a useful foundation.
Where I think the resolution of this comes from is in decision making outside Bayes. Bayesian formalism gives us in the limit of sufficient data collection, a small range of “good” parameters, that predict “best” according to the description of what kind of precision should be expected from prediction (which for Bayes is the likelihood p(Data | model))… But what we need to do with this is make a decision: do we stick with this model, or do we work harder to get another one. Whether to do that or not comes down to utilitarian concepts: How much does it matter to us that the model makes certain kinds of errors?
*ONE* way to evaluate that decision is in terms of frequency. If what we care about from a model is that it provides us with a good estimate of the frequency with which something occurs… then obviously frequency will enter into our evaluation of the model. But this is *just one way* in which to make a decision. We may instead ask what the sum of the monetary costs of the errors will be through time… or what the distribution of errors bigger than some threshold for mattering is… or a tradeoff between the cost of errors and the cost of further research and development required to eliminate them… If it takes a thousand years to improve our model a little bit… it may be time to just start using the model to improve lives today. That sort of thing.
So I see Andrew’s interest in frequency evaluation of Bayesian models as one manifestation of this broader concept of model checking as *fitness for purpose*. Our goal in Bayesian reasoning isn’t to get “subjective beliefs” or “the true value of the parameter” or frequently be correct, or whatever, it’s to *extract useful information from reality to help us make better decisions*, and we get to define “better” in whatever way we want. Mayo doesn’t get to dictate that frequency of making errors is All That Matters, and Ben Bernanke doesn’t get to tell us that Total Dollar Amounts are all that matter, and Feynman doesn’t get to tell us that the 36th decimal place in a QED prediction is all that matters…
And this is why “The Statistics Wars” will continue, because The Statistics Wars are secretly about human values, and different people value things differently.
Re: And this is why “The Statistics Wars” will continue, because The Statistics Wars are secretly about human values, and different people value things differently.
Yes, that is the case. Ironically this is more discernable in informal conversations that even in academic debates. Viewing the sociology of expertise is essential to evaluating epistemic environment — different degrees of cognitive dissonance manifest about the conflicts of interests and values. In academia, prestige is harder to garner as you all know, given the changes to university structure and incentives, over the last 30 or more years, which only have aggravated the epistemic environment. In this sense, I thought that John’s ‘Evidence Based Medicine Has Been Hijacked’ was a master presentation, for it points to how medicine is a profit-making endeavor largely.
Andrew’s blog is phenomenal as one of the few venues for the scope of topics, articles, and perspectives.
All the talk about “objectivity” in science is in my opinion a way to sidestep questions of value and usually to promote one set of values without mentioning the fact that we are promoting certain values.
“using an objective measure to select genes for further study” = “we want to study these genes and we don’t want you telling us it’s just because we like to study them”
“Objective evaluation of economic policy” = “We like the results of our study and we want to promote them over whatever you think the alternative analysis and results should have been”
If there can be only one “true objective” way to construe reality, then automatically, if you have a claim to having used it then whatever your opponent thinks is wrong…
I think the platonic view of probabilities on either side is motivated by the same goal—trying to make things “objective” by stipulation.
I think Laplace got the philosophy right that the world can be deterministic and probabilities are just our way of quantifying our own uncertainty as agents (this is not necessarily subjective). That way, you can believe in Laplace’s demon and still use probabilities to reason about your uncertainties.
Daniels
Agree with you completely
I think this is spot on:
I also believe it’s why machine learning is so popular—it’s much more common to see a predictive application in ML than in stats.
I’m also getting more and more focused on calibration and also agree with this characterization:
I wonder what Andrew thinks?
I feel like I’m doing well when Bob agrees with me.
As for predictive applications and ML etc. I think there are two senses in which we want good predictions. One narrow sense is we want to predict the results of the given process at hand… How big the sales will be if we show advertisement A with frequency F to people searching keywords K, for example (typical maybe ML application).
But also there are things where we don’t care about the predictions of the model at all, we care about inference of the parameter so that it can be used elsewhere, and this is more sciencey.
In experiments of type V (for Viscometer) the data about the duration of some fluid flow of a particular volume through a particular tube is D with fluid sampled from engine E today and D_old from samples taken yesterday, how many more days will the engine run before the viscosity reaches a level where we expect in entirely different model M that we will get damage to the engine?
And this is more what science is about. The unobserved parameters in good science are meaningful in and of themselves because they’re connected across multiple scenarios by being independently predictive of stuff about the world in a wide variety of models.
To expound slightly, because I realize this wasn’t necessarily obvious: we could have a pretty simplistic model of the viscometer, it might do a kind of lousy job of predicting the flow data through the special tube, perhaps because there’s some kind of uncontrolled clock error (a person has to press buttons on a stopwatch say, and we don’t have a good model for the person) but as long as it does a good job of inferring the viscosity after re-running the experiment with the person and the stopwatch a reasonable number of times, that’s all you’ll be using it for anyway, because you’ll be taking the viscosity you infer, and plugging it into some other model of say wear on the engine…
This is reminiscent of the parable of the orange juice: http://models.street-artists.org/2014/03/21/the-bayesian-approach-to-frequentist-sampling-theory/
the orange juice model predicts individual orange juice measurements *in a terrible way* but it converges to the right average, which is what you care about.
ML may give you *fantastic* predictions of the actual timing data from the viscometer experiment, but since it has no notion of viscosity baked in… it’s *completely and totally useless*. All of its parameters are things like “weights placed on the output of fake neuron i” or whatever.
In fact the way it gets such good viscometer predictions is probably that it internally “learns” something about the combination of fluid viscosity and muscle fatigue on the right thumb of the stopwatch holder… or something like that.
On Lakeland (lost track of the numbering)
I just want to say that the major position in SIST is to DENY that the frequency of errors is what mainly matters in science. I call that the performance view. The severe tester is interested in probing specific erroneous interpretation of data & detecting flaws in purported solutions to problems.
I thank Andrew for gathering up these interesting reflections on my Statistical Inference as Severe Testing: How to Get Beyond the Statistics Wars (2018, CUP). I was not given the reviews in advance, so I will read them carefully in full and look forward to making some responses. My view of getting beyond the statistics wars–at least as a first step–is simply understanding them! That is one of the main goals of the book. More later.
While reading this I finished off a pound of BBQ brisket. Both were delicious and both will take a good while to digest. Many thanks for hosting these discussions.
I find Owen’s discussion a bit frustrating. He frames severity as a competitor to his preferred “confidence analysis” approach and this (in my view) shows that he misunderstands what Mayo is trying to do. Owen asserts that there’s evidence for an inference if a one-sided confidence interval supports it. An anti-frequentist of whatever stripe could say to Owen, “Why are you calling that ‘evidence’? On the one hand, you have a rule with certain long-run properties and on the other hand you have a particular realization of a random variable that satisfies the rule. In what way to aggregate properties of the rule justify your specific claim here and now?” As discussed by Mayo here (1:28:28 to 1:29:37), part of the point of the severity rationale is provide an answer to this challenge, thereby justifying Owen’s preferred approach. But Owen doesn’t even see that it needs any such justification.
Maybe this is just an intrinsically hard idea to get across — I missed it on my first pass too. I guess my frustration is simply that if people can’t understand this much from what Mayo has written then they won’t have a complete enough understanding to comprehend (what I claim is) the the weak point in the severity rationale.
Interesting video. At ~ 5:30:
Ioannidis quote ~ “People claim conclusive evidence based on a single statistically significant result”
Mayo (surprised): “Do people do that!? I find that really amazing…”
Even worse than that is central premise behind 99% of the medical and social science literature for the last 70 years. They claim conclusive evidence for the scientific hypothesis…
Then a bit later someone in the audience points out “there is no mention of H* [the scientific hypothesis] for either Fisher or Pearson in your exposition”. Some discussion proceeds which doesn’t really clarify/resolve anything.
That is the problem I have with this type of stuff. It isn’t that it is wrong, it just attempts to focus on minutia while missing the elephant in the room (the connection people have been drawing between “H0” and “H*” is totally illegitimate).
Then this stopping rule thing that always comes up…
The data generating process is different if you collect 100 datapoints vs you collected datapoints until some threshold is reached. You need to use a different model for the different situations.
The likelihood needs to reflect the actual process that generated the data. You model the process you think generated the data (your theory) and then derive a prediction (likelihood) from it. Why is not only Mayo but someone in the audience acting like the only thing that could be different is the prior?
That result that held for binomial vs negative binomial sampling — the likelihood is the same for both data collection designs — hold generally. Working out the math in the normal case is an interesting exercise.
What do you mean by “generally”?
Typically the stopping rule is not “get a certain number of success/fails” like in that example, instead it is “collect data until n_min points; if p > then keep going until either you run out of money or p < 0.05”.
typo:
…if p > then keep going until…
Also, in that special case where the likelihoods end up the same I don’t see why that is a problem.
I don’t know what keeps making it drop the value. Should be:
p [greater than] 0.05
It interprets < as the opening of an html tag — to make that character appear I had to write <. (And & is also a special character, so to make < appear I had to write &lt; and so on.)
If you can make it through my blog post linked below, you’ll see a Cox/Bayes perspective on the logic of inference with a stopping rule. Think about it this way: if I tell you the data without you knowing the stopping rule you will come up with some model for the data.
Now I show you the data and you will make some Bayesian inference. You will also be able to calculate N exactly.
Now, I tell you the stopping rule, should your inference change?
In most cases, all you discover from the stopping rule is *why* you have N data points. Since you already have the data, you don’t learn anything about N for example.
Only in the situation when you can create a model in which you know something but not everything about the stopping rule will you be able to infer something about the stopping rule by using N as an additional kind of data.
For example, in your scenario, you can learn that they had more than $$$ much money because your model of the stopping is “go until you run out of money or get p < 0.05” and you saw N data points and you know that each one costs $X so they had at least $NX available…
Yes, my inference about the model I came up with should change since the denominator of Bayes’ rule changes when I “add” this new (more accurate) model.
The information you learn though is *about the experimenter* if none of the predictive equations in your model for the experimental outcomes changes, then your inference for the scientific process doesn’t change.
It can be the case that you have informative stopping rules, but this is precisely when you have a model for stopping that is less than completely certain.
Here are some examples:
I tell you my stopping rule is two H in a row, and I tell you my data is
HTHTTTHHTHT
you can calculate that I’m a liar, because I should have stopped at the 8th coin flip if I were being honest. But do you learn anything more about my coin?
Suppose I give you just “I flipped 7 times and got”
HTHTTTH
what is your model?
Now suppose I say “I flipped at least 7 times and the first 7 were”
HTHTTTH
Now suppose I say “I flipped at least 7 times, the first 7 were as below, and also I stopped after getting 2 heads and btw I stopped at the 10th flip”
HTHTTTH
Here the stopping rule and the number 10 together are informative. I can use them to infer *something* about the missing data which is an additional parameter.
I don’t disagree with this. Like I did here:
https://statmodeling.stat.columbia.edu/2019/03/31/a-comment-about-p-values-from-art-owen-upon-reading-deborah-mayos-new-book/#comment-1010811
You seem to be looking at it from a perspective I am not appreciating. I simply think that stopping rule in general requires changing the likelihood. There seem to be some cases where it works out to be the same, which I find very interesting, but not that relevant to general practice.
In a Bayesian analysis there are informative stopping rules and non-informative stopping rules. Carlos Ungil and I hashed that out quite a bit at one point. Summary was here:
http://models.street-artists.org/2017/06/24/on-models-of-the-stopping-process-informativeness-and-uninformativeness/
Yes, I would expect with typical stopping rules the likelihood is different. Eg the likelihood for the probability if sample til n = 100 vs sample til n = 10 then keep going until either p-value < 0.05 or n = 100: https://i.ibb.co/0Br6CHw/optstop.png
Code: https://pastebin.com/Nbszur1v
So I feel like I am missing something. The stopping rule discussion seems to be just about a special case where the likelihoods happen to be the same?
Yes, it is a special case. What happens is that the likelihood has two factors: (i) the probability that you stopped where you did, and (ii) the density of the data truncated by the stopping rule. It turns out that the normalizing constant of the second factor contains the parameter-dependent part of the first factor, so it always cancels out, leaving the likelihood proportional to that of a fixed sample size design.
Sorry, it is not clear to me. Are you saying this also applies to my example (sample til n = 100 vs sample til n = 10 then keep going until either p-value < 0.05 or n = 100) in the parent comment?
If so can you work it out so I can see how the stopping rule cancels out?
What if I put it this way: If I observe 80% “success” rate* wouldn’t you think the “stopping rule” model could better explain the results than the collect until 100 datapoints model?
* I see the x-axis in those plots is proportions yet labeled as percentages but you know what I mean
Yes, it applies to your example. I mean, I can work it out (or at least I could seven years ago), but I’m not going to. You’d learn more if you attempted it yourself anyway…
Ok, I find it very interesting that one could be transformed to the other via enough thought/effort. But still the likelihoods for the measured value (“% success”) are different as is clearly shown by the simulation.
The second simulation includes *lots* of outcomes where n was bigger than 10
if you have a dataset n=38 you are never in the situation where you have to compare “fixed N=10” vs “not fixed but N turned out to be 10”
Obviously if you have 35 data points you can rule out the idea that the rule was “sample until n = 10” but subset your second simulation to just the cases where the rule triggered exactly 10 data points and the p values were basically the same.
Now, if you know you were in the first case, vs you know you were in the second case, does the inference differ?
You are thinking about it completely differently than me.
Yes, obviously my inference differs since the first “case” (model) is different than the second case. You are focusing on one parameter value while I am thinking of the model as a whole.
I care about choosing the correct overall model. Look at how particle physicsists distinguished between
the “W-S” model and “hybrid/mixed” model here. The parameter sin^2(theta) could be the same but lead to different predictions from different models.
The part I think we’re confused about is that you have to *fix the data that you observe* and consider the parameter.
of course, in two different scenarios you’re likely to get totally different data… If your plan is “flip the coin 10 times” you’ll get a whole different distribution of possible flips than if your plan is “flip 10 times, then continue flipping until either p less than 0.05 against the test of binomial(p=0.5) or you get to 100”
But limit it to some specific set of data that is compatible with either model, and then try to see if you get a different *likelihood function* (ie. p(Data | model parameters) evaluated for the given Data)
Here’s what we do, we flip 10 times and filter it to results where binomial tests give p less than 0.05… this is the situation where you have fixed number of flips.
then do flip 10 times and continue until p less than 0.05 or you get to 100… and subset this to the situations where you got 10 flips….
now we imagine we’re in the situation “I have 10 flips and p is less than 0.05” would knowing which of the two processes occurred give you different probabilities over the outcomes?
I don’t understand why you would?
Likelihood is p(Data|Model). The model is fixed not the data…
My goal is simply to determine which model of the process that generated the data is best. How does doing this help me?
Isn’t it obvious that if N=38 you’ve completely ruled out the “flip 10 times” model?
so you’re only in the case where there’s any contention at all when the outcomes is compatible with both models.
This is the only case where p(Model1) doesn’t equal 0
Yes, but not the flip until n=38+ model.
Maybe I am getting this argument now. It is that we should always know the sample size (n), so every model of data generation should include n as a parameter. If you do that, optional stopping always leads to the same likelihood. Is that it?
The situation we are in is:
1) someone gives us some fixed data D.
2) For simplicity let’s say a priori p(M1) and p(M2) are both equal to 0.5
3) Model M1 is “flip exactly N times, where N = the number of times we flipped in data D” (otherwise p(Data | M1)=0)
4) Model M2 is “flip with some rule in which N is a possible outcome logically possible under the rule” (otherwise P(Data | M2)=0)
5) Decide whether M1 or M2 is the true model
Oops, and also decide what the binomial frequency f is.
It seems to amount to the idea we always need to include sample size as a parameter when deriving the likelihood from our models. My simulation histograms do not do that, which is why they look different even though the likelihood would be the same if I took that into account.
No, I still cannot accept this. Let’s say I want to find out which process generated the data (sample til 100 vs sample til stopping rule). If I observed ~80% successes I would prefer the second regardless of sample size. This is wrong?
Also I apologize to Mayo if this is a major distraction from her main points, but it was triggered by watching her lecture so…
Your graphs show frequency of Nheads/Ntotal
If you ask someone “do an experiment and report to me the fraction of heads you found” and they report “I did an experiment and found 1/3 heads” how are you going to assess this? Isn’t there a difference between “I flipped 10^6 times and got exactly 1/3 heads” and “I flipped 3 times and got 1 head” ?
basically your plot shows p(fraction of heads | experiment was run) for two different experiments. It’s very relevant if someone *only reports the fraction* not the N.
Anoneuoid:
You are taking likelihood to mean something other that what others mean by it – in particular, most think of the data as fixed with parameters varying.
This is not that uncommon and why I wrote this – https://statmodeling.stat.columbia.edu/wp-content/uploads/2011/05/plot13.pdf see appendix.
#9
A discussion of the stopping rule dropping out is Excursion 1 Tour II: https://errorstatistics.com/2019/04/04/excursion-1-tour-ii-error-probing-tools-versus-logics-of-evidence-excerpt/
#5 (to Corey’s comment)
Thanks for your point. I totally agree, but notice this has been thought to be a great big deal for many years (witness the recent Nature “retire significance” article).
My #4 comment alludes to Owen’s remarks about CIs and SEV, and why I see SEV as improving on CIs. In the ex. he discusses, the 1-sided test mu ≤ mu’ vs mu>mu’ corresponds to the lower conf bound. Interpreting a non-rejection (or non-SS result, or p-value “moderate”)* calls for looking at the upper conf bound.
* See how hard it’s becoming to talk now (that some advocate keeping p-values, but not saying “significant” or “significance”? I hope that we can at least get beyond those word disputes (but people will shout this down I suspect.)
> [Cousins’ monograph] is unfortunately a bit out of date when it comes to the philosophy of Bayesian statistics, which he ties in with subjective probability.
He seems to discuss both the “subjective” and “objective” points of view, and this paragraph sounds to me quite similar to some of your writings:
“Another claim that is dismaying to see among some physicists is the blanket statement that “Bayesians do not care about frequentist properties”. While that may be true for pure subjective Bayesians, most of the pragmatic Bayesians that we have met at PhyStat meetings do use frequentist methods to help calibrate Bayesians statements. That seems to be essential when using “objective” priors to obtain results that are used to communicate inferences from experiments.”
What I find interesting is that he seems to critique Jaynes for being too objectivistic (arguing for existence of priors representing ignorance) and too subjectivistic (ignoring the importance of having good frequentist characteristics). I may be misunderstanding the mentions, though. The subjective/objective distinction doesn’t make much sense anyway.
(BTW, the previous message was also me forgetting to complete the name/mail fields that were automatically filled in the good old days…)
Let me begin by addressing Wagenmakers who wrote:
“I cannot comment on the contents of this book, because doing so would require me to read it, and extensive prior knowledge suggests that I will violently disagree with almost every claim that is being made.”
You shouldn’t refuse to read my book because you fear you will disagree with it (let alone violently). I wrote it for YOU! And for other people who would say just what you said. SIST doesn’t hold to a specific view, but instead invites you on a philosophical excursion–a special interest cruise in fact–to illuminate statistical inference.
We set sail with a simple tool: If little or nothing has been done to rule out flaws in inferring a claim, then it has not passed a severe test. In the severe testing view, probability arises in scientific contexts to assess how capable methods are at uncovering and avoiding erroneous interpretations of data. That’s all I mean in viewing statistical inference as severe testing. I’m not saying statistical inference is always about formal statistical testing either. The testing metaphor grows out of the idea that before we have evidence for a claim, it must have passed an analysis that had the capability of having found it flawed.
We can all agree on this much, I think. SIST explores how much mileage we can get from it. The concept of severe testing is sufficiently general to apply to any of the methods now in use, whether for exploration, estimation, or prediction. I admit that none of the existing formal accounts directly give severity assessments. There isn’t even a statistical school or tribe that has explicitly endorsed this goal! I find this perplexing. There’s a difference between a claim being poorly tested (by data x) and being rendered improbable (by x), yet the difference between highly probable and highly probed isn’t highlighted in today’s statistical discussions. That will not preclude our immersion into the mindset of a strange, futuristic tribe–the severe testers. You needn’t accept the severe testing view in order to employ it as a tool for understanding and getting beyond the statistics wars. I see it as a tool for excavation, and for keeping us afloat in the marshes and quicksand that often mark today’ s controversies.
I hope that before this general discussion ends that Wagenmakers will have read just the first 29 pages. Jim Berger recently did so and I don’t think he’ll mind my sharing that he said it was “very, very good” at illuminating the current state of play and how we got here.
Here’s an excerpt that links to (proofs of) the first 29 pages. https://errorstatistics.com/2018/09/08/excursion-1-tour-i-beyond-probabilism-and-performance-severity-requirement/
I would be disappointed if people judged my work without reading it. The 1st few chapters of Deborah’s book were revelatory in some respects. It’s good to read as much background material as feasible.
To me, someone’s refusal to read other perspectives in anticipation of disagreeing with them reflects a curious habit of mind. Some scientists prejudge or show a stubbornness that is surprising.
There is plenty of probative work going in different fields. It’s that it languishes due to special interests potential to eclipse it. It is turning out that physicians themselves are critiquing allopathic medicine. Patients/consumers of healthcare have been gaining and continue to gain attention to their concerns. It’s probative.
My concern is that controversies among statisticians are being cast too narrowly as statistics ‘war’ or ‘tribalism’. Just the fewest are argumentative actually. Their otherwise wonderful research output is then less cogently evaluated. Overgeneralizations are then the standard.
#6
To a comment by Sameera Daniels
Thank you for this. I will be very sorry if Wagenmakers refuses to read any of SIST, especially because he is active in discussions on foundations (and not knowing what all sides mean really slows things down), and because I worked hard to convince him. (I hope he will at least read up to p. 29.) Now that frequentist/error statisticians seem to once again be in exile when it comes to statistical foundations, it would be generous of those holding one of the more popular views (in his case, Bayes Factors) to read a contemporary error statistical philosopher who has tried to take account of both well-known criticisms and current reform movements.
Mayo. Suppose we have two possible models for how some data occurs, M1 and M2. Suppose for simplicity that they are mutually exclusive and exhaustive (there are no other models to consider) and have similar order of magnitude prior probability (easiest is 0.5 and 0.5 but whatever, it could be 0.7 and 0.3 just not dramatically different in size).
They give us distributions p(Data | M1) and p(Data | M2)
Now suppose further that p(Data | M1) is small, say 0.05 and p(Data | M2) is large say 0.9.
then in a Bayesian posterior analysis p(M1 | Data) will be small, and p(M2 | Data) will be large.
Has a “severe test” of M1 been performed? If not, why not? If so, is there something more than this we need?
Suppose an alternative: p(Data | M1) is 0.5 and p(Data | M2) = 0.5 so that at the end, we have p(M1|Data) is about the same as p(M2|Data)… Are there situations in which you could imagine this happens and yet you’d say that a severe test could be put together and you could test these two hypotheses severely? ie. can a severe test ever be performed when the likelihood of the data under the two models is basically the same?
#8 Lakeland comment
We’re not doing likelihood comparisons. You might find an answer to your last queries in Excursion 1 Tour II here https://errorstatistics.com/2019/04/04/excursion-1-tour-ii-error-probing-tools-versus-logics-of-evidence-excerpt/
I know you’re not in general, my questions come down to: a) in your opinion are likelihood comparisons where the likelihood ratio is large a special case, ie can you use them to perform severe tests, if not why not
and b) when the likelihood doesn’t indicate a large disparity is it ever possible to get a severe test in your opinion
#26
On Lakeland query about distinguishing two equally likely models or claims.
I think maybe the gist of your question, at least (b) is this: can two equally likely hypotheses be distinguished by severity, can one pass a severe test and the other not? Let me proceed on the basis of that being your question. The answer is yes.
One of the discussions in SIST is the test of Einstein’s deflection hypothesis based on the eclipse results. The deflect effect, once it was vouchsafed to be genuine, was anomalous for Newton. Yet the Newtonian hypothesized deflection could be retained & made to fit the data, but only by means of ad hoc saves that were criticized as highly insevere ways to retain Newton. These criticisms, a combination of quantitative and qualitative severity arguments, were agreed to by scientists who regarded the Newtonian system as far more plausible. Few people at the time even understood the Einstein’s gravitational theory.
“The Newton-saving factors might have been plausible but they were unable to pass severe tests. Saving Newton this way would be bad science”. (SIST, p. 128)
We may even distinguish the evidential warrant for one and the same hypothesis H in two cases: one where it was constructed post hoc, cherry picked, and so on, a second where it was predesignated. A cherry-picked hypothesis could well be believable, but we’d still want to distinguish the evidential credit H deserves in the two cases”. (SIST, 39) On the face of it, appealing to priors can’t help, since there’s one and the same H. Or would you appeal to priors to distinguish the two cases? Or not distinguish them.
As for (a), clearly M’s being highly likely won’t suffice for M’s being well-tested. This follows from my answers to (b). Strictly speaking, any model that “fits” the data will have high likelihood. I hope that I am getting at the main issue you intend by your question. If not, you might look at Excursion 1 Tour II, linked earlier.
I read your excursion exerpt, and found
and stopped. you are discussing likelihoods, you explicitly sidestep priors, and then you complain that the result doesn’t obey probability calculus… this is because you explicitly sidestepped priors and normalization… but to form a likelihood ratio, both the prior and the normalizing factor cancel out, so the question remains in some sense. suppose we just want to test the hypothesis that theta is greater than 0.5 vs less than 0.5 and we find the integrated likelihoods, in which the normalizing factors cancel, have a ratio of 10 to 1 is this a severe test?
we aren’t testing two different models or relying on priors, just a single model and different parameter ranges… and we find a large or even enormous disparity
I recognize this may not be your preferred method, what I’m asking is do you rule out the concept of severity in this context? can I never get what you would call a severe test using this ratio of integrated likelihood method?
the main objection you give is that it’s always possible to erect a model that gives much better likelihood. and that I don’t have to prespecify the test, but here I do prespecify, a single binomial likelihood and the test is theta greater than 1/2 vs less than 1/2 and based on say 10 flips. I compute the area under the likelihood curve for theta greater and divide by the area under the likelihood curve for theta less. suppose the flips are 1011011101 the ratio of the areas is 227/29 = 7.83 or so
Mayo,
Wagenmakers’s dismissal reminds me of when Chistopher Hitchens famously said in regards to religious debates “What can be asserted without evidence can also be dismissed without evidence.” The statistics version of that should read:
What can be asserted in Statistics based on philosophy but without further evidence, can also be dismissed based on philosophy and without further evidence.
Reading Owen’s thoughts I get lost already in the first page:
“A post-hoc power analysis looks at Pr(d(X) .gt. c_alpha; mu_1).”
How is that “post-hoc”? It doesn’t depend on the observed data, does it?
Just judging by how he uses that expression in context, he doesn’t mean “post-hoc power analysis” in the usual sense. He means the post-data use of the power function to interpret experimental results. He’s talking about that because Mayo discusses that use of power in Section 5.3: Insignificant Results: Power Analysis and Severity, subsection entitled “Attained Power Π”. The equations in that section are the same as the ones in this post: Neyman, Power, and Severity.
Maybe you’re right, but he also uses the term in the usual sense at the end of the section:
“The idea of estimating power post-hoc has been criticized as unnecessary. I think that it might be useful in explaining a failure to reject H0 as the sample size being too small. A recent blog post by Andrew Gelman described how it is extremely hard to measure power post hoc because there is too much uncertainty about the effect size. Then, even if you want it, you probably cannot reliably get it. I think severity is likely to be in the same boat.”
Yeah, but there he’s just smearing severity with an equivocation. If he’d actually done the math — substituted in the actual expressions in the simple normal model Mayo always treats — I feel sure he would have noticed that the SEV function just returns the confidence coefficient for the one-sided interval you give it as the argument.
I agree that the comparison with power is a red herring and severity is more like significance. I find the name “attained power” misleading.
Looking at the formulas in that example:
* Power analysis: Pr(d(X) .gt. c_alpha ; μ1)
Power is a property of the test of the μ = μ0 hypothesis which is calculated assuming a particular alternative μ = μ1. It is independent of the data.
* Severity analysis: Pr(d(X) .gt. d(x) ; μ1)
The probability here is a property of the data which is calculated from the model assuming μ = μ1. It has nothing to do with the test of the null hypothesis μ = μ0 .
It is the probability of getting a value of the statistic more extreme than the observed value assuming μ = μ1, a.k.a. the p-value calculated from the data for the null hypothesis μ = μ1.
The description of severity analysis is therefore equivalent to (note that the “and H0 was not rejected” clause is redundant: if the p-value for μ = μ1 is high the p-value for μ = μ0 _gt_ μ1 is higher):
* Severity analysis: If the p-value for a one-tailed test of the hypothesis μ = μ1 against the alternative μ _gt_ μ1 is high, it indicates evidence that μ _lt_ μ1.
> if the p-value for μ = μ1 is high the p-value for μ = μ0 _gt_ μ1 is higher
That _greater_than_ should of course be _less_than_ instead.
I think we agree that the expressions are more general than the use to which Mayo puts them (hence the redundant clause). Her concern is with addressing criticisms of hypothesis testing (from the blog post I linked: “These assessments enable sidestepping classic fallacies of tests that are either too sensitive or not sensitive enough.”) That’s why the discussion mentions things like “null hypothesis” and “rejection” even though you can calculate the SEV function without ever knowing what the null hypothesis was and whether it was rejected or not.
I tried to make clear how, in this example at least, the proposed measure of severity is a measure of significance. I don’t say that as a bad thing (in the same way that saying that a p-value is a probability is not a bad thing). If there are other examples where severity is not significance I would be interested in learning about them. But I don’t know if there are other examples at all…
How about this angle to demonstrate my confusion:
1) It is impossible to distinguish between the two scenarios if you calculate the likelihood given the sample size.
2) If I ignore the sample size and calculate the likelihood I can distinguish between the two scenarios.
3) Mayo/frequentists claim they can distinguish between the two scenarios.
if you like we could continue this at my blog or somewhere else…
#2
Andrew: since there’s so much of interest to respond to, I’m writing quickly, but to avoid everything getting lost, I’m going to number my comments. This is #2 (although I hadn’t numbered my first which was addressing Wagenmakers).
To focus on just one of Gelman’s remarks:
“To say it another way, bringing in the title of the book under discussion: I would not quite say that statistical inference is severe testing, but I do think that severe testing is a crucial part of statistics…Severe testing is fundamental, in that prospect of revolution is a key contributor to the success of normal science. We lean on our models in large part because they have been, and will continue to be, put to the test. And we choose our statistical methods in large part because, under certain assumptions, they have good frequency properties.”
I’m glad that you say this, but I need to clarify something. The idea isn’t to view all of statistical inference as severe testing–which I don’t. The suggestion is that by viewing statistical inference as severe testing we may understand why experts disagree about how to reform statistics, and in general, we may understand what the stat wars are really all about. The disagreements often grow out of hidden assumptions about the nature of scientific inference and the roles of probability in inference. Many of these are philosophical.
What’s special about the context of severe testing is that it’s one where we want to find things out. The desire to find things out seems like an obvious goal; yet most of the time it is not what drives us. We typically may be uninterested in, if not quite resistant to, finding flaws with ideas we like. Often it is entirely proper to gather information to make your case, and ignore anything that fails to support it. Only if you really desire to find out something, or to challenge so-and-so’s (“trust me”) assurances, will you be prepared to stick your (or their) neck out to conduct a genuine “conjecture and refutation” exercise. Because you want to learn, you will be prepared to risk the possibility that the conjecture is found flawed. (SIST , 7)
Our journey requires not just the severity principle (as a minimal principle of evidence) but the assumption that we are in a context where we desire to find things out–at least during the time we are engaged in probing the stat wars.
As it happens, you’ve issued a “trust me” assurance that I would like to challenge. It’s fairly briefly stated — I’ve laid it out in a twitter thread — but I know that platform isn’t one you’re comfortable with, so if you’re open to the idea I’ll restate it here — unless you find yourself uninterested in (or even quite resistant to) looking for flaws in your own ideas.
” Often it is entirely proper to gather information to make your case, and ignore anything that fails to support it.” – so you are also concerned by information quality.
To address the point you make I would initiate a discussion of data sources, what we call Data Structure. My blog above lists two of the information quality dimensions. The full set is: 1) Data Resolution, 2) Data Structure, 3) Data Integration, 4) Temporal Relevance, 5) Chronology of Data and Goal, 6) Generalizability, 7) Operationalization and 8) Communication.
The severity test is about generalizability of findings. The decision making aspect mentioned above is about operationalisation, my comments about representation of findings are about both the 6th and 8th dimensions.
My 2019 book with Tom Redman on The Real Work of Data Science has a chapter on this aimed at data science applications https://wiley.com/go/kenett-redman/datascience
My 2016 book with Galit Shmueli titled Information Quality: The Potential of Data and Analytics to Generate Knowledge has examples from education, official statistics, risk management, customer surveys and healthcare.
For a collection of papers and presentations on information quality see http://infoq.galitshmueli.com/
and a dedicated FB wall https://www.facebook.com/infoQbook/?ref=bookmarks
To reiterate the point I made earlier. The statistics wars are engaged in part of the data driven playground. To understand it (and Mayo’s contribution), a wider perspective is needed.
#3
GELMAN: “And now on to Mayo’s subtitle. I don’t think her, or my, philosophical perspective will get us “beyond the statistics wars” by itself—but perhaps it will ultimately move us in this direction, if practitioners and theorists alike can move beyond naive confirmationist reasoning toward an embrace of variation and acceptance of uncertainty.”
MAYO: SIST does not claim to bring the rival tribes into agreement–I think there are different goals of inquiry and recall (comment #2) we’re definitely not always trying to “find things out”. I claim only to explain and unravel the sources of today’s debates. If you will look through the severity lens, just during the time you’re engaged in this journey, you will see why leaders of competing tribes so often talk right past each other.
During the 6 Excursions, you will collect “Souvenirs” A-Z (followed by a Final Keepsake). Let me reveal Souvenir Z in Excursion 6 which is titled: “(Probabilist) Foundations Lost, (Probative) Foundations Found
Souvenir Z: Understanding Tribal Warfare
We began this tour [Excursion 6 Tour II] asking: Is there an overarching philosophy that “matches contemporary attitudes”? More important is changing attitudes. Not to encourage a switch of tribes, or even a tribal truce, but something more modest and actually achievable: to understand and get beyond the tribal warfare. To understand them, at minimum, requires grasping how the goals of probabilism differ from those of probativeness. This leads to a way of changing contemporary attitudes that is bolder and more challenging. Snapshots from the error statistical lens let you see how frequentist methods supply tools for controlling and assessing how well or poorly warranted claims are. All of the links, from data generation to modeling, to statistical inference and from there to substantive research claims, fall into place within this statistical philosophy. If this is close to being a useful way to interpret a cluster of methods, then the change in contemporary attitudes is radical: it has never been explicitly unveiled. Our journey was restricted to simple examples because those are the ones fought over in decades of statistical battles. Much more work is needed. Those grappling with applied problems are best suited to develop these ideas, and see where they may lead. I never promised,when you bought your ticket for this passage, to go beyond showing that viewing statistics as severe testing will let you get beyond the statistics wars.
GELMAN: “I’ll summarize by expressing agreement with Mayo’s perspective that frequency evaluation is fundamental, while disagreeing with her focus on various crude (from my perspective) ideas such as type 1 errors and p-values. When it comes to statistical philosophy, I’d rather follow Laplace, Jaynes, and Box, rather than Neyman, Wald, and Savage. Phony Bayesmania has bitten the dust.”
MAYO: If I am to illuminate the debates and battles that currently exist, I must refer to the methods and concepts that are at the heart of so much hand-wringing, even as the goal of severity forces and redirects us to reformulate and reinterpret existing methods. (“Bayesmania”?)
It’s a reference to London Calling.
Very good Clash action!
X,
You’ll enjoy my post scheduled for 19 sept.
An accompanying workbook would have been great, Deborah. I think that pedagogy should align with the Socratic method in a manner that sharpens critical thinking more broadly. I am with Paul Rozin’s thinking with respect to the state of psychology. While Rozin focuses on social psychology, I think his observations apply to nearly every social science. And to statistics itself. The quality of theories is neglected, due in part to specialization and hyperspecialization.
As for statistics tribes, for the last three years on Twitter, I have watched the dynamics among different academic groups. There are predictable patterns of engagement, which end up sabotaging scientific engagement. For example, caricaturing others in demeaning ways with whom you disagree> might be amusing for a while but it gets tiresome over a period. Plus there all sorts of private signaling/conversations that exclude or include others.
It takes a lot of work to review past thought leaders as the ones that Andrew lists. I’m trying to incorporate as many of your suggestions as feasible timewise. Sander always has good recommendations too.
#7
To Sameera Daniels comment:
I’m teaching a seminar now and in the summer have ~15 faculty coming for a 2-week intensive. I have put lots of notes up , and if you follow the blog, you’ll see many of the chapters grew out of posts over the years with extensive comments. Are you referring to a workbook on the numerical examples or on the philosophy? I think what I’m putting together now counts as a philosophical companion.
These references correspond to the days of our current seminar meetings (not the summers).
https://errorstatistics.com/philstat-spring-19/6334-6614-captains-biblio-with-links/
Or are you talking about worked problems? Many people felt I showed too many computations. You’d need a book that teaches probability and statistics while incorporating the topics and examples in SIST. I hope that interested participants in the Summer Seminar might help to start on such a thing. Severity is introduced in A. Spanos’ new book (2019, CUP, see reference in SIST).
I plan to move into some brand new areas soon, so we’ll see.
My interest has been broader than simply statistics. I have reviewed many ‘critical thinking’ workbooks. I think that that the problems that are discussed in statistics and psychology, for example, are indicative of far broader problems in how we think. To be sure binary modes do prevail in discussions, despite best efforts to contextualize and recognize the cognitive biases so entailed in our reasoning.
I don’t think it’s simply about ‘working problems’ or achieving consensus. It’s what Steven Goodman has so cogently suggested> We don’t know yet how reform efforts will fare, if and when they are undertaken.
#4
Art Owen has many interesting points, and I’m very grateful for the careful analysis. I haven’t studied the full review yet, but one leaps out concerning a section in Excursion 5 Tour 2:
“Anything Tests Can Do CIs Do Better CIs do anything better than tests . . . No they don’t, yes they do . . .”(SIST 356)–sung to the tune of Annie Get Your Gun.
On p. 2 of his review Owen questions if severity has an advantage over confidence intervals. The example goes to SIST p. 368.
A one-sided test: mu ≤ mu’ vs mu> mu’ (say at the .025 level) corresponds to the one-sided (.975) lower bound (not upper bound); I think this is the source of the problem he raises. (This is Hoenig and Heisey’s example, as I am considering their criticism of power.) The 0.975 CI contains the parameter values that could not be rejected at the corresponding significance level or p-value (0.025): In this case, the values such that the sample mean is not statistically significantly greater than, at the corresponding level .025.
SIST 357: “We don’t deny it’s useful to look at an upper bound (e.g., 3.05) to avoid the fallacy of non-rejection, just as it was to block fallacies of rejection (Section 4.3), but there needs to be a principled basis for this move.
SIST 358 “Suppose we chuck tests and always do two-sided 1 – α confidence
intervals. We are still left with inadequacies already noted: First, the justification
is purely performance: that the interval was obtained from a procedure with good long-run coverage; second, it relies on choosing a single confidence level and reporting, in effect, whether parameter values are inside or outside.
Too dichotomous. Most importantly: The warrant for the confidence interval is just the one given by using attained power in a severity analysis. If this is right, it would make no sense for a confidence interval advocate to reject
a severity analysis.”
Discussions on the duality of CIs and tests from SIST: https://errorstatistics.files.wordpress.com/2019/04/mayo_sist_189-200244-6356-9.pdf
We can come back to this example, having made this point. I’ll also study the rest of his review.
I read the blog post but I haven’t read the book by Mayo. I have a general question though. Looking at Mayo’s publication record, I don’t see a single paper that is a pure data analysis stemming from an experiment.
I agree with the point, mentioned or implied early in the blog post, that every activity implies an implicit philosophical position, and it is better to make it explicit. Statisticians and scientists in general can’t afford to be clear about the underlying philosophy that drives their work.
By the same token, how reasonable is it for a professional philosopher to weigh in on a topic that she hasn’t gotten her hands dirty with? This is both an information question and a rhetorical one. Maybe I am wrong about this, but having done hundreds of data analyses since 2000, this has changed me in a way I can’t write down in a single summary statement or even a book. When I start a new analysis, the weight of my past experiences, which sits like unfocused compiled knowledge in my mind, drives my decision processes as I proceed with the analysis.
If someone lacks this deep background that comes from getting one’s hands dirty, and from repeatedly failing to replicate results that made perfect theoretical sense and one had strong evidence for from past data, why would I take them seriously in the first place?
I have an actual information question here. Can a football coach train a professional team of footballers despite never having played the game himself/herself? Can one become a piano teacher without knowing how to play the piano?
In statistics, there is a process of deep suffering that drives an analysis. It’s like contemplating a Zen koan for 20 years. You still don’t know the answer, but you’ve grappled with the question on the ground, in the field. You’ve faced the heat from your gurus, the advisor, the reviewer, and the editor, repeatedly and learnt from that.
For my own research problems, I do have a philosophy, and I would take seriously any philosophical positions that people with practical contact with data write about.
I’m just unsure what I can get out of abstract discussions about statistics by people like Mayo. This is not about academic qualifications, it’s about having gotten your hands dirty first. As a concrete example, if I were to sit down with Mayo and started talking about a repeated measures data-set that requires me to fit crossed subject and item random effects involving two 8×8 variance covariance matrices, I want to know first that she has experienced that first-hand and knows where most analyses will land you: in variance component hell.
Maybe I am wrong about all this and she is an expert data analyst. Just looking around a bit at her work, it sure seems to me that that’s not the case.
Maybe a constructive way to frame this is to ask Mayo to write a book consisting only of case studies, in which there is a comparison between the outcomes and decisions arising from:
– a standard frequentist analysis
– a new-statistics style frequentist analysis
– a standard Gelman style Bayesian analysis
– a standard EJ style Bayesian analysis
– a Mayo style analysis
I would buy such a book and would actually read it. Until then, I will only invest in books that teach me how to do stuff I want to do.
#20
Comment by Vasishth
You clearly disagree with Gelman’s position noted in my comment #15.
There’s no reason that all involved with statistics should care about the battles that are resulting in high pitched controversies across many scientific fields. When I speak in stat depts, I find most statisticians continue to develop frequentist methods (e.g., to cope with a variety of selection effects in constructing and appraising Big Data models) and shrug at the controversies calling for reforms and even bans. A major job of philosophers of science, on the other hand, is explaining if not also solving the conceptual problems of scientists. Since one of my focuses is on statistical science, these statistical controversies are obviously important. If I didn’t feel I had anything to say about them, I’d conclude that my philosophy of statistics wasn’t up to the job it ought to be able to accomplish. It also happens that in solving them I arrive at much more adequate solutions to more general philosophical problems of evidence, inference, induction and falsification.
That said, I might note some of the back cover endorsements:
“In this ground-breaking volume, Deborah G. Mayo cuts through the thicket of confusion surrounding debates on statistical inference, debunking the many widespread misconceptions about statistical tests and developing the theory of error statistics and severe testing. The book should be read by all practicing statisticians, and indeed by all scientists and others trying to extract meaning from data.”
David J. Hand – Imperial College, London
“…She goes beyond the usual Bayesian versus frequentist controversy and deals with pressing practical issues such as the crisis in scientific reproducibility. Whether you agree or disagree with her ideas, you will find the journey entertaining and thought provoking.”
Larry Wasserman – Carnegie Mellon University
“An extraordinary and enlightening grand tour through a century of philosophical discourse underpinning modern statistics. Mayo’s important contribution to this discourse, the severity principle, offers clarifying insight to several of the statistical conundrums all too often confounding even the brightest of modern data analysts and statistical theorists. I look forward to severity calculations eventually appearing alongside confidence intervals in statistical computer programs and journal discussions of findings.”
Steven McKinney – British Columbia Cancer Research Centre
“Whether or not you agree with her basic stance on statistical inference, if you are interested in the subject, and all scientists ought to be, Deborah G. Mayo’s writings are a must. Her views on inference are all the more valuable for being contrary to much current consensus. Her latest book will delight many and infuriate others but force all who are serious about these issues to think. Her capacity to jolt the complacent is second to none.”
Stephen Senn – author of Dicing with Death
Interestingly, most of the scientists who contact me, explaining how they are extracting ideas from my book, are engaged in very high-powered AI and machine learning. I’m learning a lot from them.
> You clearly disagree with Gelman’s position noted in my comment #15.
Someone with 2 decades of experience doing science with deep interest in following advice from Gelman and others on this blog and would like to see your ideas put into practice somehow clearly disagrees with Gelman’s position that
“There’s nothing so practical as good practice, but good philosophy can facilitate both the development and acceptance of better methods.”
are you trying to be taken seriously or just flogging your book?
Prof. Mayo, you wrote: “You clearly disagree with Gelman’s position noted in my comment #15.”
Obviously it’s not fair to expect you to read my work, but if you were to do that, you would find that, far from disagreeing from Andrew, I am trying to implement the ideas that come from the Columbia group, in which I would include people like Michael Betancourt and Bob Carpenter, and others. So, your assertion is not correct. I have even written a paper with Andrew in which I spell out one of his very important points using a specific case study!
Regarding Andrew’s particular comment, which you id’d as #15, I got a lot out of prior predictive checking, something all Bayesian textbooks mention but not a single textbook so far actually discusses the importance of in the particular case of hierarchical models with many many variance components. The specific examples the Columbia group generates led to actionable advice within my lab.
I would suggest you write a book or article where actual data is taken up and the different approaches are compared side by side. Maybe collaborate with one or more of the statisticians or data scientists that you say you learnt a lot from. Collaborate with some opponents, who can lay out e.g. the Bayesian workflow and logic as counterpoint.
For example, many of the papers in my field, you will find lovely statistically significant analyses published in top journals. Super convincing looking stuff. Then you do the EJ Wagenmakers thing and start computing Bayes factors for these studies, and boom. Bayes factors are either 1-5 (informative priors) or 200 favoring the null (uninformative priors). If you put those two results (frequentist using p-vals, and the BF approach) you will get radically different conclusions. When you use p-values you get excited, and when you use BFs, you go meh. I’ll write a paper about this soon.
Now add the Gelman approach to the above case. You’ll find that the Gelman approach of just plotting the posteriors (OK, I’m simplifying, but this is one of his advocated methods—the secret weapon) from repeated instances of an experiment design will show that *across* experiments you see a clear pattern, even though no single expt shows anything particularly informative. For me this is an important conclusion: I can do BF or p-value analyses till kingdom come on individual studies, but I’m looking at the wrong thing. I need to be looking at the pattern I see in direct replications. This furnishes serious information that allows me to move forward in my research problem.
In such a concrete comparison, I would really be interested to see what your severity testing approach adds.
The way you can address my criticism is by showing concrete case studies comparing different data-analytical methods, rather like Michael Betancourt’s and others’ case studies on github, and showing what is gained by severity testing.
You may convert more people that way than by writing abstract discussions about statistics and leaving statisticans to work out the details.
I have great respect for philosophy (growing up in New Delhi, how could one not? It’s the only way to stay sane while living there). The stoics give specific advice on what to do in each use case. But we are talking about the philosophy of statistics here, not epistemology or ontology in general, or living one’s life on a day to day basis and dealing with crises in one’s life.
Where are the use cases for statistics that use your severity testing approach? This is really your job now, you can’t outsource it to statisticians; you brought it up.
#29
Vasishth
Since we’re miscommunicating as regards the subject matter and goals of my book, I suggest, if you’re interested, have a look at the opening Tour https://errorstatistics.files.wordpress.com/2018/09/0-ex1-ti_sist_mayo_share.pdf
The specific remark to which I was alluding, in relation to disagreeing with Gellman, was his call for the importance of philosophy of science and statistics to statistics.
To make clear to potential readers the topics they’d find in the book, I created a wallpaper of words which such topics as: likelihood principle vs error probabilities, problem of induction, confirmation vs falsification, relevant of data other than the one observed, Fisher vs Neyman, model testing vs model selection, behavioral vs evidential interpretation, power: pre-data vs post-data; significance tests vs confidence intervals, Duhem’s problem, probabilism vs performance, cherry-picking data-dredging etc. etc. I have already admitted that there is no reason to suppose that all statistical practitioners would be interested in the philosophical foundations of statistics or in today’s challenges for how to reform statistics. As a philosopher of science, experiment and induction, it’s of great interest to me. I’ve also said that if you can find an example around which there has been philosophical debate that is not in my book, to please let me know. In the mean time I see practitioners engaged in strenuous debate about how to reform statistics, and they often talk past each other, unaware of a difference in underlying fundamental goals and perspectives on science. What my book does is unearth these hidden philosophical assumptions, connecting them to broader problems of how we learn about the world. Thank you.
“…many of the papers in my field, you will find lovely statistically significant analyses published in top journals. Super convincing looking stuff. Then you do the EJ Wagenmakers thing and start computing Bayes factors for these studies, and boom. Bayes factors are either 1-5 (informative priors) or 200 favoring the null (uninformative priors).”
But one could do the same thing just using a different alpha (turn sig to nonsig) so I don’t see the added benefit of using BF here to show one can take sig to nonsig.
Justin
http://www.statisticool.com
Justin:
I think your satirical blog is very funny and insightful (though I think a more general name would be apt) https://dichotomania.com/our-services
I’ve been wondering this for days… what is this satirical blog you refer to? I can’t find it from statisticool.net. I want to enjoy satire, meow!
Prof. Mayo, you wrote: “Interestingly, most of the scientists who contact me, explaining how they are extracting ideas from my book, are engaged in very high-powered AI and machine learning.”
I don’t know who these people are, but have they read Andrew’s work and tried putting it into practice? You cited some blurbs from your book where big names like Wasserman recommend your book.
I would like to see these statisticans show us what severity testing adds beyond what we can already do, in specific cases.
Just reading blurbs doesn’t impress me much because of the American (and now worldwide) tendency to overhype everything. I shrink everything I read towards zero like a good hierarchical linear mixed modeler, unless I start seeing some real information.
Personally I find it very important what to expect and what not to expect from such a book. Sometimes it’s just the “outside view” that is enlightening. There may be things to criticize that are connected to a lack of personal experience in sophisticated data analysis and mathematics (already highlighted by others was the issue that some ideas seem to be derived with a few very simple examples in mind and won’t generalize smoothly to more complex ones). But I don’t think this affects much what an open minded reader can get from the book, as long as it is not interpreted as a general handbook on how the whole of statistics should change its ways.
That said, at least she has collaborations with some very experienced data analysts such as David Cox and Aris Spanos.
I should maybe add that I’ve read quite a bit of material written by philosophers on probability and statistics, and I missed insight from proper data analysis experience much more in a number of books and papers by other authors; given the technical simplicity of the statistical issues that she actually treats, I didn’t find much that could be criticized based on “ignorance from lack of data analytic experience”.
Christian, you wrote: “given the technical simplicity of the statistical issues that she actually treats, I didn’t find much that could be criticized based on “ignorance from lack of data analytic experience””
I would characterize that as damning with faint praise. If you are referring to t-tests as the use case here, I say: yawn.
I want to see serious situations with real complexities, of the type mc-stan’s case studies cover. As you say, whether these ideas will scale is anybody’s guess. I suspect that Prof. Mayo has not encountered serious setbacks in a data analysis with a hierarchical model or mixture model (for example) that is dealing with a complex design and sparse data.
Shravan: Obviously you can say that you want to read about data analysis only from people who are experienced in data analysis and only if they tell you what to do differently in the more or less complex situations you are dealing with. You may also not think that anybody (including somebody with a background and expertise quite different from yours) can tell you anything worthwhile anymore about foundations as long as they only treat examples you find supersimple (yawn!).
Then clearly the book is not for you, and obviously you can choose not to read it. However telling Mayo that she should have written another book before even knowing what’s in hers is a bit thick, don’t you think? I’m pretty sure she won’t write a book with substantially more sophisticated case studies, because that’s not her job and not her qualification (although I should not rule it out; who am I to assess what she can or can’t do). Some statisticians may be inspired by her book and do it, maybe, maybe not. Actually there are many frequentist statisticians who, despite not using her exact formalism, do analyses that are at least in line with her philosophy (Daniel Lakens for example), also see here, although you may find these examples boring, too:
https://www.tandfonline.com/doi/abs/10.1080/00031305.2019.1565553
Christian, there’s this thing that happens: people read Mayo on severity and then round it off to the nearest thing they affirm that sounds vaguely similar. Daniel Lakens, for example, has rounded severity off to the Neyman-Pearson testing framework he advances, missing out on the advances that she claims to have made building on NP (the main one being that severity in her view blends testing and estimation). Oliver Maclaren rounded severity off to possibility theory (I had to bombard him with quotes from Mayo’s blog and Error Statistics paper to partially detach him from this idea). Some Bayesians (\me pulls at shirt collar anxiously) have been known to conflate the SEV function and the Bayesian posterior without appreciating the fact that the two expressions involve integrals defined on different spaces.
It is really not easy to understand the ideas that Mayo is trying to get across! (I know I’m treading on a minefield every time I advance an opinion about what I think she’s saying; that’s why I rely as much as possible on quoting her words directly even though it gives me an unpleasantly stalkerish mien.) I have two take-aways: first, calls to see more practical applications of these ideas from the source of them are all to the good; second, any claims by practicing researchers to be inspired by her book and to be doing work in line with her philosophy should be viewed skeptically.
This comment gibes with my own experience of trying to figure out Mayo. I’m open to the idea that there’s a way to use frequentist statistics to figure out things in a way that’s much better than the way we do it today with p values and thresholds and soforth. So I just want to see it used in some more complicated toy problems to produce numerical output that and some text describing why that numerical output is meaningful, without any fluff about journeys or Elba island or whatever. For example:
Suppose you write down 8 numbers between 0 and 1 and hand them to me. You tell me you will generate binary data using rbinom putting one of those numbers into the function. Your numbers will stream to me over a slow radio link so I’ll get one per 5 minutes…. (or you’ll send one per day by email or something)
show me as the data come in, what calculations I can do to figure out something of use about all 8 numbers, and explain to me what the calculations mean, which numbers have been tested severely or not and vs what alternatives etc
Now let’s suppose there’s a 10% pure random chance of me missing each of your transmissions… do the same thing there.
I want something as clear as Corey’s blog post about his investigations of SEV in the case where the sample space had a gap, or in a sequential trial.
or if you like, something as clear as the Stan group’s case studies… https://mc-stan.org/users/documentation/case-studies.html
Obviously I don’t think Mayo needs to do this herself, it’s not her fundamental skill, so find someone with a math-data-analysis background, get them to do it, run it by Mayo to figure out that it makes sense compared to what she thinks should be done, etc… but show me what is done.
Also, do it side by side with a few Bayesian analyses and show where they diverge if at all, and where they diverge, show why the severe testing version makes some kind of sense.
Suppose you send one every 5 minutes and there’s a 10% chance of missing, but I can detect it because it will take 10 minutes…. Now suppose you send one and after each one you wait runif(0,10) minutes and there’s a 10% chance of missing one… but I can’t detect whether I’ve missed one or not…
Also, provide R code for the analysis, and let’s be able to redo it putting in different parameters so I can see what would happen in each case…
This kind of thing is *essential* to explaining the details that you just won’t butt up against unless you try to handle something that’s a toy problem but hard enough to incorporate real-world considerations that people will really have to deal with (missing data, undetected issues with instrumentation, etc)
I rounded SEV to ‘necessity’ since
Nec(H) = 1-Poss(Not H)
while (for S2):
SEV(H) = 1 – Pvalue(Not H)
If you take Poss(Not H) = Pvalue (Not H) then you’re good. Luckily both Pvalues and possibility values are computed by maximising over composite hypotheses (see also Richard Gill’s comment). It always bothered me a bit that Mayo didn’t explicitly include/mention a max or min operator in SEV definition, though it is always invoked implicitly (you always consider the maximal/minimal probs over composites).
None of this is endorsed by Mayo of course, but it helps me remember how to calculate SEV since it often involves a lot of negation/double negatives…If people are interested in SEV I would recommend doing some of her problems using the logic explicitly.
Honestly though I mostly prefer to just do point estimation + propagated variability…
ojm, when I say “partialIy detach” I’m implicitly leaving you partially attached, aren’t I? ;-)
It was how you wanted criterion (S-1) to map onto POS(H) that most diverged from what Mayo had written. (Also how you wanted to map to pre-data error probs à la Birnbaum.)
Yeah – I still feel like Mayo should really be more dogmatic (!) about S1 given she’s all in on S2.
Otherwise examples like Cox and Hinkley Example 4.5 with a discrete parameter space mu in {0,10}, sigma =1 and observation of y=3 seem to leave the approach vulnerable.
Eg y=3 is very significant relative to mu=0. So we tentatively infer mu!=0, which implies S1: agrees with mu = 10 by definition of the parameter space, and want to assess severity.
SEV(mu=10) = 1 – pvalue (mu=0) = very high!
Which is pretty ridiculous…especially since SEV(mu=0) is even higher!
She claims that this example is ‘rigged’ or ‘artificial’ but it seems convincing to me that something more is needed. She talks about needing to ‘exhaust’ the parameter space, but I don’t see why we couldn’t be in a situation where we have two discrete possibilities.
If you instead just take Poss(H) = pvalue (H) then you get Poss mu=0) gt Poss(mu=10) but both are low. So you would report: each hypothesis has low compatibility with (possibility in light of) the data, though mu=0 is more compatible.
This is obviously not far off a likelihood analysis but arguably (by using tail probs) also allows separate rather than just relative measures of compatibility of each hypothesis with the data.
More specifically: in this example both hypotheses strongly satisfy the S2 severity requirement and appear to satisfy S1 too, but the reasoning behind satisfying S1 is too indirect. Mayo takes ‘reject H’ as a tentative positive claim for a specific ‘not H’. This indirect compatibility leads to the issue above.
IMO a better alternative is to requires direct compatibility. Eg define S1: ‘compatible with H’ as pvalue under H (= Poss(H)). In this case both mu = 0 and mu = 10 fail to satisfy S1 so the ‘counterexample’ is blocked.
But like I said, Mayo appears to take rejection of H as compatibility with some member of not H, ie satisfaction of S1 for some not H, which we then consider severity for. This indirect satisfaction of S1 leaves open undesirable examples. Direct satisfaction blocks it tho.
All of which amounts to: if you interpret pvalue (H) as Poss(H) and consider it for any H of interest you’re probably fine, at least in terms of simple examples.
Christian, it’s not that I haven’t read anything by Prof. Mayo. I tried to read her work when Andrew started mentioning it, but I couldn’t understand anything. I always felt like I had walked into the middle of a conversation and was missing some crucial assumed background knowledge.
I guess my conclusion in the past, bolstered now by the exchanges here, is that since I am able to get by very well with the philosophy behind Bayes, and since I don’t feel that I need something better, I can skip reading the book. I’ll read the first tour that Prof. Mayo points me to. I’ve long been trying and failing to understand what exactly she is proposing. As a reader, I feel I am owed some realistic (non-trivial) concrete examples. That’s all I am saying. I’m not saying she has to write a different book; a short blog post spelling out the details in a comparative manner for a non-trivial case (even something as “simple” as a 2×2 repeated measures design analyzed with a hierarchical linear model) would do for me.
I feel the same – like I walked into the middle of a conversation I haven’t been part of and don’t understand. My bad. And, judging from Mayo’s response to me, doubly so. She claims to intend the book for those that are immersed in these debates/conversations or at least those most interested in them. I think that is a shame, however, because I find the concept of severe testing a useful linguistic approach to encompassing a myriad of problems with statistical analyses. I, too, am looking for concrete examples, but I would not go so far as saying that the book is useless without them. That is why I said I wish she had written a different book.
Isn’t Mayo basically suggesting testing for model adequacy? I found her book quite challenging as a lot of it is chasing down debates in the history and philosophy of statistics, but when it comes time for her positive suggestion, it seems to be mainly model adequacy tests.
Short version: model adequacy can be contrasted with model fit. Model fit can be used to compare models via the Likelihood Ratio Test, AIC, Bayes Factors, etc. However, except in rare cases (simulations) where you know the the true model is somewhere in the set, the model fit measures only give a measure of relative fit: you can tell which model has the best fit, but there is no guarantee that even your best model is a good/adequate model. This is where model adequacy comes in. Basically you say “if this model were adequate, then X”, where X is something like “the residuals will not be autocorrelated in time” (IIRC Mayo’s example was something like this”. In phylogenetics, we use eg posterior predictive simulation, and say something like “if our best fit model is adequate, simulations from the model will match features of the observed data xyz (often summary statistics of the observed data), and if they don’t then it’s an inadequate model”. Frequentist p-values are a reasonable way to conduct these adequacy tests I think, even if you are a Bayesian or whatever for your main model comparison.
This all makes sense to me and seems reasonable, although I still worry about one thing with model adequacy/severe testing, which is that it seems like it’s semi-subjective to decide which summary statistics and adequacy tests to run. Model fit making use of the likelihood in some way seems like the more universal common ground. But there is no need to be exclusive, in phylogenetics at least, adequacy tests can be a kind of double-check to see if the best fit models still have horrible obvious flaws likely to produce misleading inference (whereas just Bayes factors etc won’t give you this).
Am I getting the gist of Mayo? Comments welcome. Ps sorry for typos I’m on my phone.
IMO your precis above is a very good summary of one of the themes of the book. (I would have to go back and check to see if I agree that it’s the *main* positive suggestion.)
#19
Hennig comment (I’ll take up his review separately).
I really appreciate your astute understanding of the goals and strategies of SIST. I invite anyone to show me an example that has been the subject of philosophical controversy that is not in SIST. It’s precisely on such simple examples that foundations have always been discussed. As Jim Berger observes, that is the only way to distinguish the underlying issues from other complexities. Moreover, I’m influenced by the way the debates and suggestions for revamping statistics has been taking place. e.g., Wasserstein felt it was crucial to keep the ASA (2016) P-value statement free of mathematical technicalities. I think it goes too far in that direction, for instance, in not delineating the requirements of an adequate test statistic in setting out statistical significance tests. The “redefine significance” movement is the two-sided normal test of mean mu with known sigma. To address the stat wars SIST must talk to those same people. I’m addressing the stat wars that I’m given. To dismiss arguments that address the examples around which the debates revolve on those grounds is a cop-out. Many of the examples in the “chestnuts and howlers” are quirky, and I show how a severe tester deals with these as well.
#30
To Christian Hennig’s comment
I very much appreciate your detailed review of my book, and your capacity to engage with these ideas. I will take those remarks up later, today is my son’s birthday. I think I’m very clear about the goals and scope of SIST and why I think it’s so urgent to tackle and help to solve the problems revolving around what I call “the Statistics Wars”. To see what I’m on about, I invite everyone who hasn’t to read the first Tour https://errorstatistics.files.wordpress.com/2018/09/0-ex1-ti_sist_mayo_share.pdf
The two most fundamental thin in statistics are questions; (1) what do you want to measure and (2) how precisely do you want to measure it. These questions enable one to select an appropriate design together with a method of data analysis. So design and analysis go together. The question of precision raises financial questions. Are you prepared to pay for your desired level of precision?
I read the book shortly after it came out. I even thought of writing a review and I thought of sending Mayo some comments – but I kept getting daunted by the magnitude of the undertaking. So, let me try not to get lost in the details here and just hit the big picture points.
I appreciated the book, but I had the constant reaction that “I wish she had written a different book.” The metaphorical journey is creative and intriguing, but for me (due to my own limitations), kept grating on me when it constantly was interwoven with historical debates (e.g., Bayes vs frequentists) so that I lost sight of the value of the metaphor. Through it all, I kept yearning for practical real examples – when they finally arrived, it looked like standard confidence intervals to me. So, I was left wondering – and still wonder – what exactly is “severe testing?”
I think this is the heart of the matter for me. The concept of severe testing is portrayed as an overarching philosophical approach that encompasses standard statistical questions as well as questions of measurement, sample selection bias, fraudulent practice, errors of logic, errors of interpretation, etc. etc. etc. In that general vein, I agree completely with Mayo and I find the idea of severity testing a valuable new language to use that encompasses many of the things that concern me about statistical practice.
On the other hand, severity testing is portrayed as a practical calculation that can be used to establish “severe tests.” This I find less convincing. The examples in the book don’t seem to go beyond what I understood confidence intervals to tell me. If I understand the thrust of the book (which I may not), then I don’t think the examples do the general point of the book any justice. You can do a “perfect” frequentist analysis using a confidence interval, interpret it correctly, and yet not have done a severe test. I believe this can be due to any number of procedural/conceptual errors. You could simply have not used a sample that could have included observations that might have led to a very different confidence interval. We can imagine many ways that could have happened. So, I see severe testing as going well beyond the standard statistical practice. But I kept wanting to see how that would work in practice. And when the book provides concrete examples, I just didn’t see how it was different than simply interpreting the frequentist intervals correctly.
I have avoided addressing the many thorny issues raised in the comments above – concerning stopping rules, likelihood ratios, etc. I realize these are very important issues – but I’m not convinced they are crucial to evaluating the severity principle. At its core, I think severity rises above all of these issues – and a number of Mayo’s comments above seem to suggest that to me. But every time we try to pin down the principle on a concrete example, I don’t see how I can apply severity in any precise way. Did I miss something (in all seriousness I ask, since the book was not an easy read for me)?
I very much like seeing this reaction and I’m curious as to how Mayo with reply to it (if she chooses to reply). I would argue, though, that there’s a tension between asserting that severity rises above all the technical issues and wishing that it were more clear how to apply the principle in concrete examples. The former is certainly the aspiration, but without the latter how could we ever say that it’s the case?
I am about here too (though only read excerpts and reviews).
Now, in my grade 9 science class, the teacher would purposely interfere in our class experiments allowing some us to see that and others not. So it was very clear the such interference would cause the experiments to fail and that one should try to discern if they would have noticed any interference from teacher. So very receptive to the severity principle but until it has endured brute force reality of undertaking to adequately make sense of actual experiments, I am holding off judgement.
Corey: “if it were in error then the test we used would have detected the error with high probability…the warrant for various inferences in the case at hand; it isn’t merely about the long run properties of the test statistic.”
I have a problem seeing how high probability comes from something other than in repeated same settings where there is smoke the alarm very frequently sounds.
#33
To O’Rourke’s comment:
These are generally hypothetical repetitions. When formal statistics enters in inquiry, it works when hypothetical relative frequencies (formalized in a sampling distribution) indicate the capabilities of methods to have unearthed a given flaw, if present. Provided, of course, we can assess and control these error probabilities.
The justification for an inference resulting from a tool with good probative capabilities, however, isn’t (merely) that it will rarely lead us astray in the long run, but because of what is indicated about the flaw in the case at hand. Likewise, a hypothesis based on, say, p-hacking has passed a lousy test, not because in the long run such a procedure performs poorly (even though this is true) but because the p-hacker hasn’t done a good job in ruling out the (known) mistaken interpretation of the data in front of us.
> what is indicated about the flaw in the case at hand
But that just seems to me to be a reference set argument – that hypothetical repetitions should be restricted to cases where there was this flaw – in the long run such a procedure as those performs poorly.
The former hypothetical relative frequencies (formalized in a sampling distribution) were misleading because the p-hacker hasn’t done a good job adequately defining the reference set …
#37
O’ROURKE: “The former hypothetical relative frequencies (formalized in a sampling distribution) were misleading because the p-hacker hasn’t done a good job adequately defining the reference set …”
A funny way to put it, but no different from saying that his p-value, or other error probability assessment is invalid. That just pushes back the question of interest (why does an illicit p-value give grounds to criticize the case at hand). My answer is that the p-hacker hasn’t done a good job in ruling out the (known) mistaken interpretation of the data in front of us. He’s done a lousy job, and has made it easy to come up with an impressive-looking effect even if spurious. As such his particular inference about the source of these data is poorly warranted.
> A funny way to put it
Not my way of putting it but it goes back to Fisher
“One of the most elusive, perhaps, is that of conditional inference. In Fisher (1959, page 78) we find the ideas of a reference set” https://projecteuclid.org/download/pdf_1/euclid.lnms/1215458835
George Casella wrote a fair amount about as did Stephen Senn in applied contexts.
#38
O’Rourke comment
No, I meant it was funny to imagine a criticism to the p-hacker being framed this way, I agree it’s another way to say that his p-value is invalid. But this is where we begun, needing to explain why an illicit p-value gives grounds to criticize the case at hand. My answer is that the p-hacker hasn’t done a good job in ruling out the (known) mistaken interpretation of the data in front of us. He’s done a lousy job, and has made it easy to come up with an impressive-looking effect even if spurious. As such his particular inference about the source of these data is poorly warranted.
“I wish she had written a different x”
To be honest I always think this about Mayo’s writing. I can’t decide if her style is just quirky or intentional obfuscation… it’s not a good place to be in. I WANT to have her provide me with a useful perspective… so far I haven’t been able to penetrate the outer shell so to speak.
Christian Hennig in a previous post here seemed to be in the same boat about the *informal* concept of severity being useful while maybe not being very convinced about the formal version Mayo has come up with.
The idea “if you set things up so you couldn’t have failed, you haven’t tested your idea against the real world” is kind of obviously true and appealing notion and seems to be related to the informal concept of severity. Unfortunately I can’t get more than that out of the concept yet.
Doing a Bayesian computation I can pre-specify which hypotheses are of interest: this is the prior. You can use a normalized indicator function if you like (flat prior), though Bayes takes this further and lets you actually *weight* the various possibilities. And then I can reweight by a function that describes how strange or not strange the data would be if the hypothesis (parameter value) were true…. this is the likelihood… and then I can renormalize the whole thing to give a new measure on a comparable scale…
I would say that as long as *some* of the parameter space is downweighted a lot compared to the maximum likelihood, that those values have been severely tested compared to the maximum likelihood value and found wanting. If the likelihood is flat, then there is no severity in the data collection and reweighting, all values of the parameter are approximately equally compatible with the data…
I think the general concept of Severity therefore applies to Bayes kind of automatically. And I don’t think Mayo agrees, but I don’t know if she has a real objection or understands the mathematical concepts here because I can’t penetrate the verbiage and I but up against ideas like:
https://errorstatistics.com/2019/04/04/excursion-1-tour-ii-error-probing-tools-versus-logics-of-evidence-excerpt/
In which it’s not clear if Mayo understands the concept of an integral… :-\
Daniel – your comment sounds like an attempt to declare that severity testing establishes the superiority of Bayesian statistics over frequentist statistics. That may even be a correct conclusion, but I somehow doubt that severity will get you there. I suspect there are a number of steps in the Bayesian analysis that would run afoul of Mayo’s severity concept – in other words, I believe her conception is designed not to award primacy to any particular statistical methodology. On the other hand, if we accept severity as a higher level, more general, concept, then I think that some statistical approaches may well make it easier to implement severity testing than other approaches. But this requires some concrete implementation of her ideas, as Keith seems to require above. I do think it would be a useful exercise to accept the general premise of severity testing and then embark (yeah, I can use the journey metaphor as well) on describing how various statistical methodologies might either assist or impede with implementing that concept. At some point, it will have to involve some concrete kind of evaluation (perhaps “testing” is best dropped as a goal) to see whether some methodologies lend themselves better to the goal of being severely tested.
Having just written that, perhaps “severity testing” should be changed to “severity evaluation.” I’ll await Mayo’s thoughts on all of this.
No, that’s not what I was trying to say. What I was trying to say is, I don’t think Mayo thinks Bayesian stats is even compatible with a concept of severity, and yet I see a concept that seems related within Bayes and I don’t understand why she seems to dismiss it.
I don’t know the specifics of this case, but a lot of science is one researcher disagreeing with another just because that’s what we do, no deeper reason.
The instinct is to say no, that’s wrong. Sometimes, my students write a draft of a paper, I read it and say, why did you write X and not Y? They then revise the paper. I read it again, having forgotten the last version. Now I ask, why did you write Y and not X? Happens every time.
#16
Comment by Dale Lehman.
I use the term “severe testing” not severity testing. The term severity is Popper’s even though he never adequately cashed this out (something discussed in SIST, Excursion 2 Tour II). I’m not wedded to it. It could be stringent probing, or error probing. Using “evaluation”rather than “testing” is fine too. What might we use instead of “severe testers”–you know that tribe whose members are keen on probing for mistakes.
I do like the ‘journey’ metaphor for that is how I have proceeded across different domains and disciplines. In short an intellectual adventure. I believe that Wittgenstein and Charles S. Peirce had that same attitude, judging from reading their biographies. Perhaps Frank Plumpton Ramsey too. All eclectics. Their output was not as prolific as their contemporaries. Bertrand Russell and others at Cambridge included them, despite their being controversies over their approaches.
I would argue though that ‘probativeness’ is exercised in different degrees in different fields. Moreover, as I may have mentioned before, and obvious, fierce questioning has been occurring. The Evidence-Based Medicine movement is one influential movement. There are Cochrane initiatives and several others.
It’s the public that will have to be part of this conversation as a consequence of appeals to larger and larger clinical trials. They are clinical trial participants after all, with the greatest stakes in treatments. Do they need to be philosophers of science as well? What do you think?
My primary observation is that there is far too much didacticism in nearly all approaches. And the jargon within are a big hindrance to understanding theory and practice.
In fact, post data D you could define integrate(-log(p(D|q)/p(D|qmax)) * p(q) dq) as the prior predictive “severity” for the realized data, since it measures the average degree of downweighting that you’re doing over the prior measure for parameter q… ie how strongly are you ruling out some options on average?
#17 Comment by Lakeland
Does anyone else have a problem with those sentences? It’s an essential task of the book to clarify concepts that are often confused. People often confuse the likelihood of H (given x) with the probability of H (given x). That’s because in informal English, likelihood is often used interchangeably with probability. Now the best ways I can think of to do this are on pp 30-1, there are three. Please suggest a better way. I do understand the concept of an integral.
Sure, people often confuse the concepts. Sure, likelihoods evaluated at particular data are not probabilities in general… but then we’re explicitly not asking for Bayesian probabilities…
The point is this: I can form L(Data ; theta) as a function, and I can calculate integral(L(Data ; theta) for theta greater than 0.5) and integral(L(Data ; theta) for theta less than 0.5) and then I can ask whether the ratio of these two is relevant to anything regarding severity.
Is it? If not, why not?
The Neyman-Pearson Lemma establishes likelihood ratio tests as the uniformly most powerful test for point hypothesis, so if you like I’m happy to just test the hypothesis say q=0.75 vs q=0.25…
Let’s say you are generating random numbers with a computer and you tell me you’ve either put 0.25 or 0.75 into your computer… I’m supposed to test which one you’re using.
Can I or can’t I use a likelihood test to form a severe test? that’s all I’m trying to figure out, not other facts about likelihoods such as that they need to be normalized before they satisfy probability axioms or that they’re independent of sampling plan or etc.
About the only thing I can do in this case where you’re generating random numbers and I’m trying to figure out whether you put 0.25 or 0.75 in your computer is ask you to give me different sample sizes… so I think regardless of what you do:
a) a sample of 1 will not be severe for any test
b) a sample of 1 million will be severe for basically any test anyone would think of…
If you reject the likelihood ratio test as ever being severe regardless of whether we do say 1 million samples… I’d like to know why, and if you don’t I’d like to know why… I just would like to know what role likelihood can play in testing.
Daniel: “Christian Hennig in a previous post here seemed to be in the same boat about the *informal* concept of severity being useful while maybe not being very convinced about the formal version Mayo has come up with.”
My perception is that the informal concept of severity is much wider than the formal version. In particular, informal severity is about a piecemeal approach, as Mayo calls it, about testing different aspects of a theory and maybe even testing the same aspect more than once, whereas formal severity is defined in the framework of a single test. Actually, the thing is not so much that I’d not be convinced about formal severity. I think that it is a useful concept that would deserve more elaboration and maybe amendment for cases like Corey’s. However, parts of the book may give the impression that formal severity as defined by Mayo is meant as a 1:1 formalization of the informal concept, but there is far more to the informal concept than what is formalized. Actually the formal definition doesn’t address the question whether a hypothesis is overall severely tested or not. It only is about what can be ruled out based on the information of one dataset used in one test.
#39
To Hennig (on his comments)
I noticed you had several exchanges this morning, and I found there was no more room to reply, so I’m writing here, as it is relevant. Thank you so much for clarifying so many points and replying to queries. I agree in the most fundamental ways with everything you wrote, with some qualifications. I wouldn’t say formal SEV is limited to a single test, insofar as formal methods are combined in statistics, SEV would go there too, or the severe tester might go with some new combinations. Don’t forget, as well, that I distinguish “big picture” inference, which is inference, given everything that is known in an inquiry, not just the specific data. You might remind Lakeland that the severity assessment is not a kind of epistemic probability (I’m not sure but he seemed to be suggesting that). It’s an assessment of well-testedness. Highly probable differs from highly probed.
Also of possible relevance are some index entries:
severity
disobeys the probability axioms, 423
when not calculable, 200
severity requirement/principle
in terms of solving a problem, 300
The introduction of severity for solving a problem is an additional formal use that I did not have before, at least not explicitly. I’d be interested to know what you think of it.
I’ve sketched some responses to your excellent review, but I’ve been kept busy with the queries from comments, and am still finalizing our Summer Seminar.
“I wouldn’t say formal SEV is limited to a single test, insofar as formal methods are combined in statistics, SEV would go there too, or the severe tester might go with some new combinations.”
My understanding is that you can define a “combined procedure” from several tests and then compute SEV for that (which basically makes the overall procedure “one single test”), so far I agree. You can also compute severity for several tests and get several SEV-values. But all examples and definitions I have seen were based on one testing procedure, the performance characteristics of which would determine the SEV. Did I miss something?
“Infinitely many values for θ between 0 and 1 yield positive likelihoods; clearly, then likelihoods do not sum to 1, or any number in particular. Likelihoods do not obey the probability calculus.”
I am very curious what statisticians like Wasserman, and other people who endorse the book on the back cover, think about statements like these. These are worrying red flags and should raise some doubts in the reader’s mind about how much the author understands what they are writing about.
I’m also curious as to what Andrew thinks about this kind of statement and what it implies about the level of understanding Prof. Mayo might be at currently. Maybe it’s not important, maybe she doesn’t need to understand basic theory in order to make her point; I don’t know. But it makes me uncomfortable. It’s like being taught to play the piano by someone who doesn’t know how to play it herself.
Male doctors can be gynecologists.
Why someone having a “Doctor of Philosophy” degree cannot digest a philosopher’s point of view?
Knowledge comes from theory (Deming). All theories must have a philopsohical foundation.
Perhaps you disagree with the way Mayo put the point, but it’s a fact that the likelihood function is not (in general) a probability function. That is, L(x, phi), as a function of phi, is not probabilistic, so that (for example) the integral of L(x, phi) between phi1 and phi2 does not represent a probability.
It is, of course, possible to (arbitrarily) normalize L(x, phi) so that it integrates to 1 (assuming it integrates to some finite number). But that doesn’t mean L(x, phi) is probabilistic. In fact, you can normalize L(x, phi) to any arbitrary constant you want. I’m pretty sure that’s Mayo’s point when she says “likelihoods do not sum to 1, or any number in particular.”
The fact is that all finite measures are isomorphic to probability, so as long as it integrates to something, it may as well integrate to 1.
“so as long as it integrates to something, it may as well integrate to 1.”
I assume you mean, “so as long as it integrates to something *finite*, it may as well integrate to 1.”
I reserve judgement for finite but unlimited nonstandard integrals, but otherwise yes ;-)
And I don’t think this is just technicality, much of the reason p values and confidence intervals “work” IMHO is that they often correspond to renormalized Bayesian posteriors from nonstandard (flat) priors.
But you don’t really need to go there to ask the question: can you use a ratio of integrated likelihoods in a useful manner some of the time? I’d just like to hear some kind of severity position on this question, because for finite ranges in almost all real world cases, the integral of the likelihood over the finite range of interest is finite and nonzero, and so the ratio of the likelihood integrals exists and is finite even if you can’t normalize the likelihood.
If this quantity has meaning in a “severe testing” context, then it’s a pretty short step to the Bayesian posterior…
and if the quantity has no meaning, then how is it that the uniformly most powerful frequentist test (likelihood ratio test via Neyman-Pearson lemma) fails to even be admissible for severe testing?
Zeno says that integration is just another model that is … sometimes helpful but ultimately wrong.
Daniel: “can you use a ratio of integrated likelihoods in a useful manner some of the time? I’d just like to hear some kind of severity position on this question, because for finite ranges in almost all real world cases, the integral of the likelihood over the finite range of interest is finite and nonzero, and so the ratio of the likelihood integrals exists and is finite even if you can’t normalize the likelihood.
If this quantity has meaning in a “severe testing” context, then it’s a pretty short step to the Bayesian posterior…”
What I think is that you can define a testing procedure based on it, and then you can compute error probabilities (of type I and II; SEV values are basically such error probabilities with the reference H0 pushed around based on what other parameter values you may be interested to make statements about, and the critical value chosen as the observed data) and every assessment of severity will start from that. So yes, the quantity can have a use in severe testing, although its use is not different, in principle, from what can be done with any other test statistic. (It may be optimal, good or not so good but theoretical assessment of the quality of tests is NP-business, not Mayo’s.)
Christian, thank you for that, for the moment I’ll take your position as the severe testing position.
now, anything you’ve just said doesn’t rely on special facta about the likelihood, so it applies to the Bayesian posterior as well. The next question is how do you define “error probabilities” in this context.
let’s say I have a statistical model with some parameters and I am interested in whether q is greater than 1 say because it indicates some benefit of a drug or the like. I compute the posterior probability that q is greater than 1 and tentatively accept this as true if the probability is greater than .995 say… I consider this whole procedure as a test of the drugs efficacy. (nevermind that I disagree with this usage and prefer utilities for the moment)
I’ll further stipulate that my entire Bayesian model is epistemic, and makes no effort to fit frequency of outcomes because we collect too few data points to validate any sampling distribution we might stipulate (say we have 25 patients). so I’m unwilling to let you calculate what would happen in repetitions using the posterior predictive distribution of my model since it doesn’t model accurately the frequency of outcomes. but let’s say that I do believe such a stable frequency distribution exists
now, what is the probability of me making an error using my above decision rule for my test?
I’d like to point out that it either is true that the drug helps people on average, or it isn’t. so I have either made an error, or I haven’t. there is no model for the sampling distribution of my decision, so to compute it approximately you will need to rerun my experiment say 100 times and see how often it did make an error… and this of course means we must know what the truth is, so we’d better run the experiment another 1000 times to find out what the real truth is…
how severe is such a test?
I believe that to the extent you can say severity exists, it would have to be an unknown number, as the stable frequency distribution is unknown and we can’t do the 1000+ replications of the experiment.
I further believe that this is true of the vast majority of all statistical analysis in experiments in science. the reason for statistics is that we haven’t got the truth
Daniel: If I get your setup right, for given q you can compute the probability that in fact your model will yield a posterior of >0.995 (or smaller, or whatever) that you will accept q>1.
Severity doesn’t use priors but depends on the parameter. It also depends on the data through your observed result. So let’s say from the observed data together with your prior settings you got a posterior of 0.998. My understanding is that if you can show for *any* fixed parameter value q=0.998 for q>1 is very small, then your decision q>1 is severely tested (SEV is probably one minus the probability maximised over q<=1, but this is not checked against Mayo's writing and you should never trust anything that I write down from my memory). This regards the SEV formal function; as I had written earlier, informal severity would require more than that, like model assumption checking; maybe also looking at whether the result reproduces or is rather caused by some measurement artifact etc.
Sorry, it seems some of my posting was eaten. The second paragraph should have been:
Severity doesn’t use priors but depends on the parameter. It also depends on the data through your observed result. So let’s say from the observed data together with your prior settings you got a posterior of 0.998. My understanding is that if you can show for *any* fixed parameter value q=0.998 for q>1 is very small, then your decision q>1 is severely tested (SEV is probably one minus the probability maximised over q<=1, but this is not checked against Mayo's writing and you should never trust anything that I write down from my memory). This regards the SEV formal function; as I had written earlier, informal severity would require more than that, like model assumption checking; maybe also looking at whether the result reproduces or is rather caused by some measurement artifact etc.
Bugger! Again! Apparently some sign I used there is not allowed. Let’s try once more…
Severity doesn’t use priors but depends on the parameter. It also depends on the data through your observed result. So let’s say from the observed data together with your prior settings you got a posterior of 0.998. My understanding is that if you can show for *any* fixed parameter value q smaller or equal than 1 that the probability of obtaining from your data a posterior probability larger or equal than 0.998 for q>1 is very small, then your decision q>1 is severely tested (SEV is probably one minus the probability maximised over q<=1, but this is not checked against Mayo's writing and you should never trust anything that I write down from my memory). This regards the SEV formal function; as I had written earlier, informal severity would require more than that, like model assumption checking; maybe also looking at whether the result reproduces or is rather caused by some measurement artifact etc.
Daniel, Mayo says: “In order for a reported P-value to even be legitimate, assumptions must hold approximately. Ability to test & affirm this requires a certain sample size. If that checks out, the difference at level p indicates a smaller discrepancy from the null, as can also be seen with a CI.” She also says that in the sort of situation you’re outlining one can say that the severity is unknown or that it’s low (she prefers low), but the real point is that it isn’t high. I expect she would disagree that it is thus for the “vast majority of all statistical analysis” (or at least that it is *necessarily* true); she would say that you can test the auxiliary assumptions severely as is Spanos’s misspecification testing approach and that passing such tests is what secures the approximate accuracy of the severity calculation in the primary inference of interest.
Christian. I have a model Data = some_function(Observables, a,b,c,q) + error
I assume some form for the error *as epistemic probability* I calculate posterior for a,b,c,q and marginalize to q and calculate epistemic probability p(q > 1 | Data, Model), and decide to tell people “my drug has benefit” if p(q>1 | Data, Model) is itself large such as 0.998
How am I to calculate the frequency of having made an error? I assume Mayo only works with frequencies, so I’m going to split the terminology frequency/epistemic probability.
I can’t calculate this frequency without assuming some frequency distribution for the event “the bayesian posterior gives p(q > 1 | Data, Model) after running experiment and doing calculation”. This frequency distribution must either be assumed over the binary outcome, or be assumed over the data and its consequences simulated for example.
Either one is pointless, because it leaves me in a position where I either use binomial with unknown f and have to infer f using many physical replications of the experiment… or it leaves me in a position where i need a frequency model for error and calibrating that requires that I collect vastly more data than I did.
There are cases where the frequency distribution can be assumed because we have a large enough sample size, but they’re cases where we basically “don’t need statistics” like if you sample 1 million people randomly from the social security administration, track them all down, and ask them their income last year, you’ll get a distribution of incomes that’s precise enough that we can calculate anything we like…. of course as soon as you subset by male, between ages of x,y and with certain income living in certain state… that fact goes away.
A major thing to understand is that the SEV function assesses severity based on one specific test and as a function of what you observed. It isn’t a measure of how hard you tried, so before observing the SEV function won’t tell you anything. However for the informal assessment of severity it is important also how hard you tried to disprove your hypothesis, i.e., how many aspects in which it could be wrong you actually tested, and whether you used well powered tests for doing that.
Re Daniel, 10:47 am:
“How am I to calculate the frequency of having made an error? I assume Mayo only works with frequencies, so I’m going to split the terminology frequency/epistemic probability.
I can’t calculate this frequency without assuming some frequency distribution for the event “the bayesian posterior gives p(q > 1 | Data, Model) after running experiment and doing calculation”. This frequency distribution must either be assumed over the binary outcome, or be assumed over the data and its consequences simulated for example.”
You’re right; it’s the second. This harks back to some earlier discussions we had about frequentist modelling.
“it leaves me in a position where i need a frequency model for error and calibrating that requires that I collect vastly more data than I did.”
You don’t need more data. You can calculate severity for more than one model, not assuming that any one of this is true. I have tried to explain to you earlier that “assuming” a frequentist model doesn’t mean that I indeed have enough information to be sure that it is more or less true. However this raises the issue of robustness. What if another model is true that still allows some interpretation in terms of the parameter of interest q?
So you can at first look at your epistemic models and ask for the probability of making a wrong decision if they were in fact frequentist true models, with q smaller 1. Of course you don’t believe that this is true, but it is a reasonable thing to ask as first guess. Then you can play the same game with other models that also involve q smaller 1 but are different in some sense, for example t-distributions instead of normals, or with some dependence between observations. Obviously you can’t exhaust all possibilities. Some possibilities will give approximately equal results to what you try, so you don’t need to bother about them. There may be some others that allow your posterior for q larger than 1 to be large despite corresponding in fact to q smaller than 1 in terms of interpretation. If this is the case, you can’t rule these out with severity, which is actually very informative for your Bayesian analysis, because it means that there are frequentist models that in fact would correspond to q smaller 1, however would lead, under your epistemic setup, to a posterior larger than 0.998 for a wrong q! So if these were indeed true (which you can’t know unless you rule them out by other means), they would lead your Bayesian analysis astray.
This is logically all fine for me, the only problem (which is a problem for frequentist and Bayesian analysis alike) is that the space of possible models is full of weird things and we can’t check them all.
>So you can at first look at your epistemic models and ask for the probability of making a wrong decision if they were in fact frequentist true models, with q smaller 1.
I don’t think Mayo would admit this. But suppose we do, and suppose we include all the various modified models we’re likely to care about within a Bayesian mixture model (ie. the t distributed errors and the dependencies and etc).
Now, Bayesian models are automatically calibrated with respect to themselves (ie. when generating process is the real process). So if we put the posterior predictive distribution in and we simulate data and run our model, unless I’m missing a subtlety, if the generating process is treated as actual process for data, then the posterior distribution of q is a calibrated frequency distribution as well, and so the frequency of making the mistake we made is the same as the posterior distribution and .995 is the probability that q greater than zero with .005 the probability of an error.
Under this theory, every bayesian result of this type (where there’s a high probability of parameter q being bigger than 1 etc) is a severe test of the hypothesis under the assumptions.
Next we have to ask whether the assumptions have been severely tested, as Corey points out… So we choose some test statistics and calculate with them to determine if the assumptions we made in the model were valid… except we need to test them against an explicit alternative… and we included all possible models that were considered worth considering into the Bayesian model. The alternative is “something else” which is basically non-explicit… so there is nothing to test it against…. if there were, we’d add it back to the Bayesian model and get a different posterior and need to test the frequency asssumptions there against again…. “something else” which isn’t explicit.
As far as I can tell, severity is either compatible with Bayes, in which case when I use Bayes to form my tests it IS Bayes except using something like a posterior probability threshold to make a claim, or it’s completely incompatible with Bayes in which case it’s only applicable when I have something like a central limit theorem which gives me an explicit form for the frequency distribution of observed statistics dependent on only weak assumptions about the data, because otherwise it will go into an infinite regress of needing to assess the goodness of the fit, and then assess the severity of the goodness of fit test, and then assess the severity of the severity of the goodness of fit test….
Furthermore in huge numbers of cases the goodness of fit is simply unable to be assessed severely… Like that recent map of political prejudice. To assess frequency issues in such a case will require having a reasonably well calibrated adequate frequency model of the answers to the prejudice questions in each county… which means at least say 100 samples of questionnaires in each county, times…I just looked it up, about 3141 counties in the US… so around 314000 questionnaires. But we could afford to collect 2000 questionnaires so to assess severity of this kind of thing we need to have about 160 times as much money as we have to do this study.
By which point you wouldn’t need to do statistical analysis, you’d just calculate the averages and don’t bother putting standard errors on them who cares at that point, it’s pointless to speculate because in almost all cases we have *nowhere near* the resources to do just the very basic check required to decide whether we’re ready to do severity evaluation.
Daniel: As I said before, the SEV calculation will *not* tell you whether you tested your hypothesis severely (informal meaning) but rather only whether you can severely rule out *specific* models by the data you have.
“Now, Bayesian models are automatically calibrated with respect to themselves (ie. when generating process is the real process). So if we put the posterior predictive distribution in and we simulate data and run our model, unless I’m missing a subtlety, if the generating process is treated as actual process for data, then the posterior distribution of q is a calibrated frequency distribution as well, and so the frequency of making the mistake we made is the same as the posterior distribution and .995 is the probability that q greater than zero with .005 the probability of an error.”
I don’t get this. This probability is computed under a Bayesian mixture that allows for both q smaller 1 and q larger 1, so *under this model* it is not clear what the true q is supposed to be.
The idea of an error probability is that we look at a model under which the hypothesis is either true or false (what is true is defined by choosing the model to look at), we look at a decision rule, and then we ask, what is the probability that this rule gets it wrong. This model cannot be a Bayesian mixture that mixed over situations that can be both, true or false, because if such a model would be true in reality, it wouldn’t involve a true value of q because both alternatives are possible under the model. So it is not clear what under this model an erroneous decision would be.
What you could do is mix over only those distributions that have q<1 and compute a probability for having the posterior for q larger 1 larger than 0.995 (or whatever you observe). This should be small. However, even in this case you have only severely excluded this specific mixture, not everything you have mixed over.
"I don’t think Mayo would admit this."
Chances are you can find a quote of hers that you can use to argue that (I actually know which, probably what Corey had quoted before), however I think she should, and no harm can be done (in her view). Because if you can severely rule out a distribution with a specific parameter value, it isn't worth arguing whether model assumptions are fulfilled or not (they may not be, however this isn't important because the specific distribution is already killed for that other reason). Furthermore, severity as a concept surely should also apply if your sample size is too small to nail down any model at sufficient precision, to show what you can still and what you cannot rule out. Even arbitrarily small samples serve to severely rule out something; you ask for N(0,1) and observe 1000, model is dead already from n=1.
there is a subtlety… while the Bayesian generator will use q < 1 the correct fraction of the time, the Bayesian fit performed on such data could have whatever frequency of getting the wrong answer… so the calculation is complicated.
once again I’m wishing for some specific nontrivial example problems… all the ones I’ve seen involve Corey finding out that severity does weird stuff… like
https://itschancy.wordpress.com/2018/02/19/everything-i-never-got-around-to-writing-about-severity/
Daniel: One of the key ideas of severe testing (informal use of term) is that you try hard to find something that would disprove your ideas. So if you set up a Bayesian model which gives out a posterior for q and you’d infer q>1 from a larger posterior, the interesting question is: Can you actually set up a frequentist model that you can’t rule out from your data, that would be interpreted as having true q<=1 (for example, with q being the median of a t-distribution, if in your Bayesian model you have normals), but would give you a high probability for observing such a large posterior for q larger than 1 (under your epistemic model) that you'd actually infer that q larger than one holds?
Just looking at your Bayesian epistemic model and stating that you're right with high probability within that model is rather weak.
>Just looking at your Bayesian epistemic model and stating that you’re right with high probability within that model is rather weak.
NO DOUBT! which is why I’d really like to see a nontrivial usage of severity in a context that’s realistic and doesn’t involve knowing the precise distribution of the data etc. Something “simple” like inferring the proportion of families in each county in the US whose post-tax income doesn’t cover rent, utilities, food, and transportation to work given their county and family structure (say age and sex of each person living in the household) using the entire ACS microdata dataset. It’s high quality, it’s large, and it contains answers to relevant questions. Let’s also just make the question simple, is the proportion of people in California who fail to meet this requirement larger or smaller than the proportion of people in Arkansas?
As I see it, every claim of knowing something about the shape of a distribution can be cashed out in terms of knowing something epistemically delta-function-like about some number of hidden parameters.
for example suppose f(x)=sum(a[i]*L_i(x)) is a series formed of standardized legendre polynomials with say N terms, then if r(i) is a uniform(0,1) random sequence, x(i) = A*f(2*r(i)-1)+B can have basically any distribution you like. Saying that it has some specific distribution is basically equivalent to saying that you know all N+2 numbers in the expansion
Occasionally we have something like a central limit theorem which tells us things like sum(x(i),i=1,k) will have a nearly normal distribution regardless of the individual x(i) distributions as long as they’re not too weird. In this kind of case you *can make a legitimate claim* to knowing all of the legendre coefficients… but in the general case of doing something like extrapolating the results of a survey in which it matters how the individual data points are distributed in order to make it so that all the different predictions for sliced and diced extrapolations make sense… when you assume some form for the frequency distribution of measurements in the population, you’re inventing delta function priors over thousands of parameters as *physically real facts about repeated surveys in the world*
sorry, I don’t buy that. This is how you cash out Jaynes’ mind-projection fallacy into math.
And if you calculate severity with one of these distributions, you wind up with a fact about Weirdlandia not reality.
Now, in a Bayesian model, you wind up with probability about facts about your model of reality (ie. the probability is over the parameters), in a frequentist analysis you wind up with precise probability facts about the frequency of occurrence of things in a fictional place virtually guaranteed to be different in many ways from here.
Daniel: Well, chances are we won’t come together anymore in this life regarding the role and meaning of models…
It’s probably not helpful to repeat myself once more but I can’t help myself… you don’t need to know a “true model” at any precision, there don’t need to be any such thing, to do something regarding severity. You only need to specify models, *any number of them*, that make some sense to you, and see whether the data rule them out.
I get that part, I just think that frequentist analysis is presenting as being about facts about the world, such as “based on our 100 person survey, if you were to survey *all* the people in this county you would find that more than f=15% of them are food insecure according to the given definition of food insecurity, and this claim has been tested severely compared to f less than 15%”
But this is really a statement: “In a world in which we know as much about the shape of the distribution of food consumption as if we had in detail measured it for 5000 people in this county (1/3 the population) and found it to be exactly a normal distribution with exactly the standard deviation s we could use that meta-information together with our 100 person survey to rule out that f was less than 15%”
Notice how much better this sounds when you consider it in terms of simple measurement error with a highly calibrated instrument, where you can cash out the distributional information produced for you by the factory:
“Using a mass spectrometer calibrated by the factory to read accurately with error normally distributed about 0 +- 1ng we measured each of these 100 samples of water and found that using the assumptions given by the intensive factory calibration we could rule out with a high degree of severity the idea that more than 1 of the samples had more than .75 times the threshold of allowable lead”
When we have distributional information from calibration procedures performed on instruments… frequentist statistics makes perfect sense to me.
Yes, the likelihood function may as well integrate to 1, but it may just as well integrate to any other number because the likelihood is only defined up to a multiplicative constant. Thus “likelihoods do not sum to 1, or any number in particular,” just like Mayo said. A probability function, on the other hand, must sum to 1.
#34
Olav’s comment.
Yes.
I don’t think that conclusion (“Likelihoods do not obey the probability calculus”) is being disputed. But the argument used (“Infinitely many values for θ between 0 and 1 yield positive likelihoods; clearly, then likelihoods do not sum to 1, or any number in particular.”) is plainly wrong, it’s not a matter of agreement or disagreement. One could use the same argument to say that continuous probability distributions do not obey the probability calculus.
Yes, the argument, as stated, is clearly bad. However, when someone makes a bad argument, you can interpret that in charitable or uncharitable ways. Here are some of the options in this particular case: (1) Mayo has no idea how integrals work, (2) Mayo absent-mindedly made a mistake in this particular case, (3) Mayo expressed herself in an infelicitous way and there’s a good argument in the vicinity of the bad argument that was actually expressed. I was suggesting that (3) may be the case (i.e that she was just making the point that likelihood functions, in contrast to probability functions, integrate to (i.e. sum to, since integration is a kind of summation) an arbitrary number).
it’s worse than that though Carlos, because this is in a paragraph in which she has just explicitly suggested that we avoid a Bayesian take. first she says avoid Bayes and consider likelihoods alone, and then she dismisses likelihoods because they don’t provide Bayesian probabilities using an argument that is meaningless. even if we are charitable about the integration thing, the point is a non sequitur, we’ve just agreed for the purposes of argument to consider whether likelihoods alone can do something for us by earlier stipulation, and then have been told that they can’t because they don’t provide the thing we’ve already stipulated is not needed…
are likelihoods useful for statistics by themselves? this is the question, and she ducks it by saying they aren’t normalized… WTH? as a lawyer would say, objection, nonresponsive…
Shravan:
This is a fairly standard *standard* position “The likelihood is the probability of the observations for various values of the parameters and will be denoted as c(y) Pr(y; theta), where Pr is the tentatively assumed probability model that generated
the observations, the observations y are taken as fixed and the parameter theta is varied. … A more formal definition of likelihood is that it is simply a mathematical function L(theta; y) = c(y) Pr(y; theta).
The formal definition as a mathematical function though, may blur that the likelihood is the probability of re-observing what was actually observed. In particular, one should not condition on something that was not actually observed such as a continuous outcome, but instead some appropriate interval containing that outcome (i.e. see page 52 of Cox & Hinkley)” In the appendix, here https://statmodeling.stat.columbia.edu/wp-content/uploads/2011/05/plot13.pdf
Further to this, the likelihood function is a (sufficient) statistic but has no calibration on its own. Much of David Cox’s career centered on get distributions for likelihoods so that they would be calibrated. So those likelihood quantities that have been calibrated could be used to get severity but not otherwise.
#18
Lehman comment
I think the important differences (and also close connections) between severity assessments and CIs have been taken up in some of my other comments. What I do in SIST is simply examine the examples that are and have been the focus of philosophical controversy (the stat wars). If you can find an example that has been the focus of philosophical controversy that I omit, please let me know. As I say on p. 145 “You might say, assessing severity is no different from what we would do with a judicious use of existing error probabilities That’s what the severe tester says.” I never would have bothered if this judicious use of error probabilities was common. Instead we see devastating criticisms of methods which, to the severe tester, are easily remedied using their own resources, along with the severe testing perspective.
You might also notice how severity serves on the “meta-level” to critically evaluate other methods. See for example p. 258 and p. 263. If people weren’t seriously proposing–or even adopting– these alternatives as ways to improve statistical practice (as regards these very examples) and solve replication crises, I would never have felt the need to examine them in this way.
#11
Brian Haig’s review of SIST.
Haig is one of the few people who has a sufficiently strong background in the statistical and philosophical issues, as well as being immersed in the current stat wars in psychology. I very much appreciate his interesting synthesis of SIST, and his own willingness to revise his standpoints on important issues. He’s written a great review and I hope he gets to publish it! I’ll note a few points for discussion:
HAIG: “Further, the error-statistical outlook can accommodate both evidential and behavioural interpretations of NHST, respectively serving probative and performance goals, to use Mayo’s suggestive terms. SIST urges us to move beyond the claim that NHST is an inchoate hybrid. Based on a close reading of the historical record, Mayo argues that Fisher and Neyman and Pearson should be interpreted as compatibilists, and that focusing on the vitriolic exchanges between Fisher and Neyman prevents one from seeing how their views dovetail. Importantly, Mayo formulates the error-statistical perspective on NHST by assembling insights from these founding fathers, and additional sources, into a coherent hybrid.”
I do hope there’s a move away from rehearsing the incompatibilist presuppositions, as it robs Fisherians from notions they need (e.g., power) and N-P testers from a data-dependent assessment. Recognizing that Neyman developed both tests and CIs–even at the same time–should scotch this tendency. Yet notice how this “family feud” is at the heart of the recent move to stop saying “significance”, while retaining P-values and CIs, perhaps renamed as “compatibility intervals”. Kempthorne and Folks (1971) had “consonance intervals” long ago. Why not just report: which parameters values is x statistically significantly greater than at levels .9, .95, .99, etc. The severe tester must always indicate what inferences are not well warranted. This leads to reporting corresponding CI claims at, say, ..5, .6, .7 confidence levels.
#12
Brian Haig’s review
HAIG: “The standard account of confidence intervals adopted by the new statisticians prespecifies a single confidence interval (a strong preference for 0.95 in their case). The single interval estimate corresponding to this level provides the basis for the inference that is drawn about the parameter values, depending on whether they fall inside or outside the interval. A limitation of this way of proceeding is that each of the values of a parameter in the interval are taken to have the same probative force, even though many will have been weakly tested. By contrast, the error-statistician draws inferences about each of the obtained values according to whether they are warranted, or not, at different severity levels, thus leading to a series of confidence intervals. Crucially, the different values will not have the same probative force.”
MAYO: One thing that isn’t sufficiently clear: our inferences are not to points in the interval, but to inequalities like mu x-bar is warranted with SEV = .5, even though x-bar is the most likely value for mu.
#12a typo in #12
my > x-bar
V
#13
HAIG: “These Bayesians criticize NHST, often advocate the use of Bayes factors for hypothesis testing, and rehearse a number of other well-known Bayesian objections to frequentist statistical practice. …They also need to reckon with the coherent hybrid NHST produced by the error statisticians, and argue against it if they want to justify abandoning NHST; they need to rethink whether Bayes factors can provide strong tests of hypotheses without their ability to probe errors; and they should consider, among other challenges, Mayo’s critique of the Likelihood Principle, a principle to which they often appeal when critiquing frequentist statistics.”
MAYO: The issue of the Likelihood Principle (LP) is fundamental, thus it appears early on, in the second half of Excursion 1. I am perplexed that people who purport to be quite concerned with selection effects (multiple-testing, data dredging, p-hacking) would promote the LP which tells you that the “sampling plan” (& thus error probability control) is irrelevant. Rejecting the relevance of the sampling distribution post data is at the very least in tension, if not inconsistent, with providing a justification for registered reports, yet they are lauded as one of the most effective means to achieving replicable results. The critical reader of a registered report would would look, in effect, at the sampling distribution: she’d look at the probability that one or another hypothesis, stopping point, choice of grouping variables,etc. could have led to a false positive–even without a formal error probability computation.
Haig challenges Bayesians to consider your critique of the Likelihood Principle. I have looked at the two concrete scenarios in which you examine the LP through the lens of severity here. In the first, your criticism is founded on an error; in the second, the criticism may bite against likelihoodists but is toothless against Bayesians.
Sorry for an off-topic question, but I see you have mentioned Aris Spanos’s methodology in another comment (to which I do not see a way to respond directly). I have a related question posted on Cross Validated, perhaps you could contribute there? https://stats.stackexchange.com/questions/303887/effects-of-model-selection-and-misspecification-testing-on-inference-probabilis
#40
Hardy query (not off topic, but people should look at the discussion you link to on Spanos on Cross Validated).
I know Hennig is asking questions along these lines in his review, and I’m remiss in not attending to them. The points from Spanos to which you refer (on Cross Validated) are indeed relevant, and I will bring your query to his attention. I’ve thought a lot about this as part of the general question as to when (alleged) double-counting and data dependent claims are problematic, and when not. We know they cannot always be (see SIST for many examples). In the land of testing stat assumptions, one needs to distinguish two main things: (1) the adequacy of the statistical model for purposes of asking a subsequent claim—getting the error probabilities approximately correct so that the severity of the primary inference can be assessed. (2) The adequacy of an inference in the case of an M-S test of a substantive model.
Some things I say about (1) are in SIST 319-20: an inference about a statistical model assumption is not a statistical inference to a generalization: It’s explaining how given data might have been generated, and is akin to my category of explaining a “ known effect,” (discussed elsewhere in SIST) only keeping to the statistical categories of distribution, independence/dependence, and homogeneity/heterogeneity (Section 4.6).
The aim of predesignation, as with the preference for novel data, is to avoid biasing selection effects in the primary statistical inference. Here data are remodeled to ask a different question. Strictly speaking our model assumptions are predesignated as soon as we propose a given model for statistical inference.
Parametric tests of assumptions may themselves have assumptions, which is why judicious combinations of varied tests are called upon to ensure their overall error probabilities. Ways are devised to “keep track” of the error probabilities.
M-S tests in the error statistical methodology are deliberately designed to be independent of (or orthogonal to) the primary question at hand. The model assumptions, singly or in groups, arise as argumentative assumptions, ready to be falsified by criticism. In many cases, the inference is as close to a deductive falsification as to be wished. Granted, respecifying a model for a substantive end, (2), is more complicated, and depends on the goal. I wonder in this connection how Gelman can view a respecified model in his own interesting approach as merely deductive–as he seems to (but I may be wrong here).
The argument for a respecified model is intended to be a convergent argument: questionable conjectures along the way don’t bring down the tower (section 1.2). Instead, problems ramify so that the specification finally deemed adequate has been sufficiently severely tested for the task at hand.
Nice, thanks for that summary of the Spanos ideas, which as you describe them I agree with mostly! See discussion with Hennig above:
https://statmodeling.stat.columbia.edu/2019/04/12/several-reviews-of-deborah-mayos-new-book-statistical-inference-as-severe-testing-how-to-get-beyond-the-statistics-wars/#comment-1016340 and preceding.
So, Mayo’s collaborator seems to agree with me, we can only make severity assessments when we can first make fairly strong distributional assumptions that have been tested to be adequate? And by the way, we should question potentially whether these adequacy tests were themselves severe should we not? And then to assess severity on the adequacy tests we should have a statistical model of the frequency distribution of modeling errors by this statistician… and so on and so on
as one of my grad school friends said about another’s lab experiments: (approximately) “What we need here is a stochastic model of a female Iranian graduate student and a tabletop triaxial soil testing machine”
To which I replied (approximately) “But first we must have a stochastic model of a Belgian postdoc building mathematical models of a Female Iranian graduate student with a tabletop triaxial soil testing machine”
When the statistical model arises from a central limit theorem type mathematical proof, and ONLY THEN do we avoid an infinite regress by simply checking some mathematically verifiable facts about the world, such as for example that our measurements of pressure are bounded by the maximum one gets before the machine explodes, and therefore whatever the output of the machine if it has a stable distribution it has moments of all orders and therefore sample averages through the CLT are normally distributed for large enough samples… etc
In the absence of an attractor such as this, every test of adequacy just gets us farther and farther down an infinite regress of testing the adequacy of the adequacy test…
#41
To Lakeland Comment.
Please see my reply to #40, no infinite regress, else we could never falsify claims.
Can you explain for example how if I have a survey of 100 random people in a county giving their before tax income, and age and sex of each person in their household, together with a separate dataset showing the caloric intake of a wide variety of people and their activity level and weight, and a large database of ticker transactions in local food stores, I could create a frequency model of say their food security distribution (let’s say it’s measured in terms of after tax income minus cost of healthy food required for their household based on a caloric requirement model) and then assess the adequacy of this food security distribution and then give a severe test of the hypothesis that more than 15% of people in the whole county are food insecure (negative value of after tax income minus cost of healthy food for their household) compared to the hypothesis that less than 15% are insecure?
I obviously don’t need you to build the model in detail, just a sort of outline of the procedure perhaps it would look like:
1) build caloric needs model using expert input for c function:
observedcals(sex,age,weight) = c(s,a,w) + error_distrib
2) validate error_distrib assumption using adequacy tests A(actual_error_histogram, predicted_error_histogram)
3) Build cost of food model using ticker data and input from nutritionists: cost(sex,age,weight) = ticker_cost_of(typical_meal(c(s,a,w) + error_distrib)) + ticker_cost_error
4) validate(ticker_cost_error_histogram) using adequacy measure
5) Build taxation model: taxes(income, location, family_composition) + tax_error_frequency
6) validate tax_error_frequency somehow
7) For each respondent, calculate family food requirements, calculate family cost of food from food requirements, calculate family after tax income from reported pre-tax income and estimated taxes, calculate difference between post-tax income and food costs…
8) Validate histogram of post-tax food insecurity
9) now calculate severity from validated histogram of insecurity and assess severity of test that fraction is greater than 15%….
Can you fill in a few blanks here, as to how the distributional assumption validations might look or what techniques might be used at each step? Maybe just even types of tests you could use, and why they would be reasonable.
I’m no expert on Spanos’s approach — I’m pretty negative on Spanos’s explanations of his MS testing framework for the reason given by Björn in your link. To me it seems that a lot of the claims he makes for the approach can and should be cashed out in math and turned into theorems. Propagation of error is neglected — the possibility of error in the tests that check the secondary assumptions is handled by resort to verbiage like “judicious combinations” and “secure the statistical adequacy of the primary inference” and not actually checking what could happen when passing test results are in error.
Corey: I have thought about this quite a bit, and actually I’m doing some work on this with a PhD student. There is also already quite a bit of work exploring the impact of MS testing on subsequent model-based inference. My current view is that it can strongly depend on the setup. In some setups Spanos’s statements are pretty much in line with what we find, in others not so much. Surely at times he makes some overoptimistic marketing statements that are easy to criticise.
Referring to what Daniel wrote at 4:25pm, I indeed believe that Spanos is too optimistic regarding how strongly we can nail down the model, and that in this respect my philosophy/way of doing things indeed deviates from his and from Mayo’s as far as she is with Spanos on that issue. (And Daniel seems to like what Spanos writes more because he can use it better to argue that frequentist modelling very rarely makes sense, with which I wildly disagree, and Spanos will disagree with this as well, except that he fuels it to some extent.)
Christian, I think it’s great that someone with a more charitable view than mine is looking into this. It’s fairly easy to see that everything works as described when ancillary statistics or easy orthogonalizations exist. I find the combination of claims of general applicability and the waving away of difficult cases just too annoying. (And I’m perfectly aware of the irony of a Bayesian saying that.)
#44
to Corey’s comment
Let me remind people that one of the most important functions of a severity critique is to block BENT (bad inferences, no test) cases. Revealing problems and gaps with statistical assumptions or with presuppositions in linking statistical inference to substantive problems is just what a severe testing account ought to do. Remember too that severe testing is intended for the context where we’re trying to find something out and are striving to avoid mistaken interpretations of data (as opposed to, say, making our case). I even recommend and suggest ways to block, if not also to falsify, some of the measurements or types of inquiry we see. “A hypothesis to be considered must always be: the results point to the inability of the study to severely probe the phenomenon of interest. The goal would be to build up a body of knowledge on closing existing loopholes when conducting a type of inquiry.” (SIST 104). An idea I take seriously is building what I call a repertoire of errors and mistakes in generating and interpreting data.
A major theme with which I agree in today’s movement to cope with the ‘statistical crisis of replication’ is that statistics is not alchemy!
https://www.tandfonline.com/doi/full/10.1080/00031305.2019.1583913
it cannot turn knowledge gaps, limits of theory, let alone slipshod or lousy science, into good science. It would be much more effective and honest to discredit the flawed studies, and even falsify types of measurements and fields of inquiry, than to blame the tools, the perversity of incentives or other scapegoats. We should learn from our mistakes!
Mayo, I put it to you that error probabilities are not the right tool for the job of blocking BENT cases because they can block inferences that are obviously correct. The first step along the path to seeing this (or to rebutting my claim) is to reply in the affirmative to this query.
Corey just keep repeating the Severity Philosopher’s mantra:
Hard tests for thee,
But not for me!
Very rarely makes sense in certain really important contexts, makes perfect sense in others. I mean, for example when an instrument has been calibrated to give certain kinds of measurements with certain kinds of stationary error distributions… we can use that fact ! it’s very useful.
When questions about what might happen under other circumstances can be answered by directly subsampling from a large data set, hey that’s incredibly useful…
when math theorems guarantee asymptotic results and we have large numbers of data points, hey that’s useful too!
And although sometimes this “big data” issue comes along with sufficient lack of bias to make just a large set of data enough to answer our questions using descriptive statistics and maybe a little bootstrapping… it’s far too often not the case. For example even though we had hundreds of polls of thousands of people, pollsters still mis-predicted the last US election, and that’s even though they did go to a lot of trouble to *try* to get some kind of large unbiased samples. Often just bias sneaks in, and we don’t know what its frequency distribution is even approximately, or we have to calculate complex functions of unknown future quantities that don’t even have a sampling distribution, like the taxes each individual corporation in the S&P 500 will pay on their next quarter income.
#14
HAIG: “Although researchers and textbook writers in psychology correctly assume that rejection of
the null hypothesis implies acceptance of the alternative hypothesis, they too often err in
treating the alternative hypothesis as a research, or scientific, hypothesis rather than as a
statistical hypothesis. …SIST explicitly forbids concluding that statistical significance implies substantive
significance.”
First, a “rejection” of a test hypothesis (a better term than null, although its brevity results in my using it) should be seen as a formal shorthand for the actual inference which can take many forms (the taxonomy in 3.3). One might be: “the data indicate a discrepancy g from Ho.” It should not be an inference to ‘accepting” anything, except that that is a shorthand. It’s very disappointing that a straw-lady version of tests, whereby a rejection or a stat sig difference from Ho, is taken as evidence for a substantive hypothesis H*, is the primary criticism of error-statistical tests of hypotheses. The probability of inferring H* erroneously is not bound by the small P-value (or Type I error in a N-P test), even where we assume it is valid.
Second, the fact that some fields fallaciously move from stat sig to H* should not be the basis for condemning tests. SIST opens with the well-known slogan: statistical significance is not the same as substantive significance. H* may make claims that haven’t probed in the least by the statistical test, and so the inference to H* lacks severity. Neyman and Pearson (N-P) tests are explicit in avoiding such fallacies by considering the alternative statistical hypothesis H1, such that Ho and H1 exhaust the space of statistical hypotheses. The ASA (2016) statement on P-values makes no mention of N-P tests or power. (One may still commit fallacies with N-P tests, such as inferring a discrepency of a larger magnitude than is warranted. The severity interpretation of a rejection (or small P-value or whatever) is designed to prevent this.)
Yet the move from a stat sig effect to an H* that entails or “explains” the stat sig effect does constitute a “Bayes-boost”. That is, the posterior on H* would be boosted by the stat sig result. Likewise, H* could occur in a Bayes Factor or likelihood ratio. So the supposition that the fundamental abuse of statistical hypothesis tests is avoided in these alternative approaches doesn’t hold up.
#15
HAIG: “From a sympathetic, but critical, reading of Popper, Mayo endorses his strategy of developing scientific knowledge by identifying and correcting errors through strong tests of scientific claims. . . . A heartening attitude that comes through in SIST is the firm belief that a philosophy of statistics is an important part of statistical thinking. This contrasts markedly with much of statistical theory, and most of statistical practice. Given that statisticians operate with an implicit philosophy, whether they know it or not, it is better that they avail themselves of an explicitly thought-out philosophy that serves practice in useful ways.”
GELMAN: “I agree, very much.
To paraphrase Bill James, the alternative to good philosophy is not “no philosophy,” it’s “bad philosophy.” I’ve spent too much time seeing Bayesians avoid checking their models out of a philosophical conviction that subjective priors cannot be empirically questioned, and too much time seeing non-Bayesians produce ridiculous estimates that could have been avoided by using available outside information. There’s nothing so practical as good practice, but good philosophy can facilitate both the development and acceptance of better methods.”
MAYO: I concur! Let’s hope we see philosophers of science interacting with statisticians on issues of philosophical foundations in the future. An editor who wanted to craft an article on the reactions by philosophers to the recent call to “retire significance” couldn’t find takers (aside from me). Changes on the side of statisticians are also needed, as Gelman urges.
» Mayo:
“An editor who wanted to craft an article on the reactions by philosophers to the recent call to “retire significance” couldn’t find takers”
What editor was that, if I may ask? I’m working on a paper that is just such a reaction, and I’d love to know who would be interested in publishing it. :)
Brian Haig says:
I thank Deborah and Andrew for their positive remarks about my “review” of SIST. I‘m heartened by the fact that three of us emphasize the importance of the philosophy of statistics, and the philosophy of science more generally, for deepening our understanding of statistical theory and practice. It’s a great pity that there’s a decided reluctance by both statisticians and scientists to make constructive use of philosophy to do this. This is certainly the case in my discipline, psychology. Even when articles in psychology list “the philosophy of science” in their Key Words, they mostly shy away from engaging the relevant philosophical literatures. As Deborah and Andrew know well, the theoretical psychologist, Paul Meehl, was deeply informed by the philosophy of science, and did pioneering work on the value of metascience (the science of science) for better understanding scientific processes. It is a bit ironic that the recent enthusiasm for metascience among methods reformers in psychology, and elsewhere, fails to recognize, or make use of, Meehl’s work in these two overlapping fields.
I have computed severity curves from simulated data for both high and low power situations. Since severity is computed post data (compared with power which is estimated pre data) it occurred to me that the severity curves might be telling me no more than a confidence interval. It also occurred to me that there might be a one to one correspondence between severity curves and confidence intervals, but I haven’t tried to prove as such. I work under the assumption that a given set of data contains a finite amount of information which can be used to address a statistical question, and that the purpose of the statistical analysis is to extract this information in order to answer the question. If severity manages to extract more information than mare established methods then it means that for 100 years we have been using inefficient methods – which I rather doubt.
Peter – two comments to your entry:
1. You too seem concerned by information quality. I already wrote about this above as presenting a wider perspective than the statistic wars.
2. The classical power analysis is focused on the statistical test you plan to implement. There are many aspects of the study design that are not necessarily accounted for in such power calculations. Gelman and Carlin offer a semi empirical Bayes simulation based approach to assess Sign type error on significant outcomes. I particularly like the fact that this allows to better account for study design considerations (Gelman, A. and Carlin, J. Beyond power calculations: assessing type S (sign) and type M (magnitude) errors. Perspect Psychol Sci. 2014;9;641-651).
Deborah – Since you quoted David Hand. Here is an extract of the foreword he wrote to our book on information quality: “I am often invited to assess research proposals. Included amongst the questions I have to ask myself in such assessments are: Are the goals stated sufficiently clearly? Does the study have a good chance of achieving the stated goals? Will the researchers be able to obtain sufficient quality data for the project? Are the analysis methods adequate to answer the questions? And so on…. These questions are precisely the sorts of questions addressed by the InfoQ – Information Quality – framework…But the book goes beyond merely providing a framework. It also delves into the details of these overlooked aspects of data analysis. It discusses the fact that the same data may be high quality for one purpose and low for another, and that the adequacy of an analysis depends on the data and the goal, as well as depending on other less obvious aspects, such as the accessibility, completeness, and confidentiality of the data. And it illustrates the ideas with a series of illuminating applications.” These remarks capture the wider perspective on statistics wars I mentioned above.
I am struck by the following quoted from from E. J. Wagenmmakers
“I cannot comment on the contents of this book, because doing so would require me to read it, and extensive prior knowledge suggests that I will violently disagree with almost every claim that is being made. In my opinion, the only long-term hope for vague concepts such as the “severity” of a test is to embed them within a rational (i.e., Bayesian) framework, but I suspect that this is not the route that the author wishes to pursue. Perhaps this book is comforting to those who have neither the time nor the desire to learn Bayesian inference, in a similar way that homeopathy provides comfort to patients with a serious medical condition.”
There are ethics to argument. One is that you use the same standards of clarity and rigor for views you support as for those you oppose. Another is that you avoid disparaging analogies unless you can substantiate the details. “Probability” is intensely vague–nobody has ever seen one–but we mathematize it, apply it, converse about it; sometimes we even reason about it: why should “severity” be any different?
#22
Glymour comment.
So nice to have a philosopher of science jump in here! I agree with you.
Clark:
It’s too bad that you did not have the time to comment on Mayo’s book, but I appreciate that E. J. shared his reactions. He was open about his perspective and where it is coming from.
#23
Fleshing out my reply to Glymour
I want to note that I do define severity very clearly. A claim passes a severe test to the extent that it has been subjected to and passes a test that probably would have found a specific flaw if present. The capability of the test to have revealed flaws if present gives us the severity assessment. In formal statistical contexts, error probabilities of methods can but need not supply relevant severity assessments. (I explain the situations in which they do so in SIST.) In informal contexts, we build informal arguments from coincidence as with my weight example on 14-15.
#21
Kenett comment.
I’ve no doubt there are wider topics than the stat wars, but it’s pretty wide wouldn’t you say? I’ll look for your book on info quality.
On your remark on Gelman and Carlin (2014) “Beyond Power Calculations…,” perhaps you’ll look at exhibit (vii) p. 359 of SIST where that paper comes up. See if you agree with how I reconcile an apparent tension with severity.
#24 to Chapman comment
I give a link to sections that relate SEV & CIs in my #4 comment. Also relevant, I say in SIST p. 356:
“Let’s admit right away that the error statistical computations are interrelated, and if you have the correct principle directing you, you could get severity by other means. The big deal is having the correct principle directing you…” In the example discussed in #4, you need a principle to avoid fallacies of non significant (“moderate” p-value) results. Attainted power or SEV (or something else) can give it to you). It’s not a matter of digging out more info, but avoiding misinterpretations of results–the very ones that people are so upset about.
I haven’t read the book yet, and may never have anything to add even after I do, but i wanted to thank Deborah, Andrew and all the other commenters here for thoughtful, civil and interesting discussion.
#25
On Andrew Gelman:
I’m glad that Gelman alludes, near the start of this post, to Gelman and Shalizi (2014), a really important and influential paper. “I’ll also point you to my paper with Shalizi on the philosophy of Bayesian statistics”. I had wondered if he would distance himself from that joint paper, written with an error statistician, in light of recent events in the stat wars. Gelman and Shalizi say:
“What we are advocating, then, is what Cox and Hinkley (1974) call ‘pure significance testing’, in which certain of the model’s implications are compared directly to the data, rather than entering into a contest with some alternative model”. (p. 20)
“When Bayesian data analysis is understood as simply getting the posterior distribution, it is held that ‘pure significance tests have no role to play in the Bayesian framework’ (Schervish, 1995, p. 218). The dismissal rests on the idea that the prior distribution can accurately reflect our actual knowledge and beliefs…. The main point where we disagree with many Bayesians is that we do not see Bayesian methods as generally useful for giving the posterior probability that a model is true, or the probability for preferring model A over model B, or whatever. Beyond the philosophical difficulties, there are technical problems with methods that purport to determine the posterior probability of models, most notably that in models with continuous parameters, aspects of the model that have essentially no effect on posterior inferences within a model can have huge effects on the comparison of posterior probability among models.” (p.22)
“It is possible to do better, both through standard hypothesis tests and the kind of predictive checks we have described. In particular, as Mayo (1996) has emphasized, it is vital to consider the severity of tests, their capacity to detect violations of hypotheses when they are present.” (p. 28)
Now I know Andrew will say as he has explained before, that what he advocates is very different from knocking down a straw null of no effect and (fallaciously!) moving to infer evidence for a substantive theory or effect.
“Model checking, on the other hand, corresponds to the identification of anomalies, with a switch to a new model when they become intolerable.” (30)
But however the test results are used, so long as it is not fallacious, it is still serving its role in indicating, first an anomaly (with what’s expected were the data to have been generated as described in the given model), second, that the anomaly is a genuine effect–having seen the anomaly persists—and finally, at some point, that it’s “intolerable” and we move to new models. But there’s more than one way to account for a genuine anomaly. So here too the inference is open to error: it is a statistical inference, even if restricted to the source of these data. Granting that in model checking the “real anomaly” that is indicated is at a lower level of generality than in finding an anomaly to a full blown theory, statistical hypotheses tests (not “isolated” tests, but combined )may be used for both. And even at the lower level of statistical model checking, significance tests or p-value reasoning is doing work. So, if Andrew abides by what he says in Gelman and Shalizi, then we agree that significance tests can show the existence of anomalous effects, and can be the basis for statistical falsification.
Deborah:
Yes, I do think that significance tests can be valuable, if the purpose is to find flaws in a model that we want to use, rather than to shoot down a model we don’t care about, with the idea that this provides evidence for a preferred alternative.
#27
To Andrew
Yes, we’re talking about a non-fallacious use of statistical significance tests, not one that moves from a statistically significant result, even if genuine, to a scientific claim that hasn’t been well-probed thereby.
By the same token, significance tests can be valuable, if the purpose is to find flaws in the presumption that a drug or treatment we want to use is beneficial (and doesn’t cause, say, increased risks of heart disease or breast cancer, as with the trials of hormone replacement therapy [Prempro] in 2002.
Thank you.
Deborah:
For the example in your second paragraph I would just use Bayesian inference and estimate the risks directly.
#28
To Andrew
Even if you think there’s another way to have found the same information, it still follows that the randomized controlled trials and analysis by statistical significance tests are informative about the existence of a genuine effect. They wanted to know if the effect was real, even if small.
The observational studies had been taken to show HRT was beneficial for all these diseases. Some worried, correctly it turns out, that those studies were open to the bias of “healthy women’s syndrome,” and groups of women in congress called for RCTs. So I take it the prior in favor of benefit would have been high. Everyone was shocked.
https://www.washingtonpost.com/archive/local/2002/07/11/halting-of-hormone-study-met-with-fear/a3c9d577-2a5d-4800-995e-ff437e7800ad/?utm_term=.d9d79b4d55d9
http://www.nbcnews.com/id/16206352/ns/health-cancer/t/breast-cancer-drop-tied-less-hormone-therapy/#.XJr6W2RKi2x
I will return to commenting on the reviews of SIST that I didn’t get to.
Deborah:
1. Randomized controlled trials can be great; I’ve never disagreed with that, and that is orthogonal to the above discussions. RCTs are valuable in Bayesian or non-Bayesian inference. See chapter 8 of BDA3 (chapter 7 of the first editions) for discussion of the relevance of randomization for Bayesian inference.
2. I don’t think it makes a lot of sense to say “the existence of a genuine effect” . . . “if the effect was real, even if small.” I think it makes more sense to estimate the effect and how it varies.
3. As we have discussed in a thread elsewhere, I accept that null hypothesis significance testing can solve problems, when it is used carefully. I don’t think that null hypothesis significance testing is the best tool for the job, and I think that, as the jobs become more complicated, it becomes a worse tool, but if it’s the tool that people have, it can be useful. The question, “Can null hypothesis significance testing be useful?” is not the same as “Is null hypothesis significance testing fundamentally answering the right questions?”
I think too, with the deflection of light experiments, that the prior for Newtonian was probably very high.
Justin
http://www.statisticool.com
From what I can read here, haven’t read the book yet, nobody even touched on the main issue:
Few people disagree that dichotomous thinking in the face of uncertainty is risky and makes you uncomfortable. That’s exactly the point! Resisting it is arguing yourself out of a job. Very few intellectual jobs come without the need to take difficult decisions and own them. That’s why it is called taking on responsibility.
The need to make binary decisions when data is uncertain is a feature of reality, not frequentist statistics. Whatever statistical techniques will prevail in the end, they will *still* need to take binary decisions based on uncertain data. otherwise they’re just not very useful if they can only solve the easy cases where either a binary decision isn’t needed or data isn’t all that uncertain or both.
To me this view reflects a blurring or confusion of, one the one hand what (we think) we know, and on the other hand, the courses of action available to us. There are two distinct and sequential steps here: first, understand what the available data are telling us about the true state of the world, and only then, figure out which of the available options is best. Dichotomous decisions do not require dichotomous thinking — they only require utility functions that have a binary action set.
The current standard NHST approach doesn’t require dichotomous thinking of the kind that you dislike, so I take it you do not have problems with keeping it?
I don’t accept the premise of your question as phrased, so perhaps you’d like to explain more fully in what way you think the current standard NHST approach doesn’t require dichotomous thinking of the kind I dislike.
David:
Lots and lots of my work is not about the need to make decisions. Indeed, the most important parts of my work, the places where I’ve made the most contributions to the world, have very rarely involved decisions (except in the tautological sense that I made a decision to write this book or that article or whatever, but those decisions are not made in any statistical way so I don’t think they’re relevant to our discussion here).
You write, “The need to make binary decisions when data is uncertain is a feature of reality.” It’s a feature of some reality, only some. Just for example, one of my first research projects was estimating the effect of incumbency in congressional elections. We got estimates and standard errors, made plots, did some things to assess the reasonableness of our model assumptions, but binary decisions did not come up. We did “take on responsibility” in this project: we made strong claims and staked our reputations on them, and our work had influence.
I’ve also done work in pharmacology. People at the companies involved are making decisions about what lines of research to pursue and how to invest their time and money. I don’t think I’d be doing them any favors by trying to make strong deterministic statements based on noisy data, and I don’t think I’d be doing them any favors by using noisy and nearly irrelevant tail-area probabilities or binary statistical-significance statements to summarize complex and costly data. As a statistician, I want to help these people learn from their data. I don’t want to be tied down by old-fashioned statistical methods that are used to create a false sense of certainty.
Finally, yes, I’ve done some research where my colleagues and I make decision recommendations; see this radon project, for example. There we make decisions using decision analysis, based on estimates of costs, risks, and probability. Statistical significance does not come into it at all.
When you write those books, that is of course related to decision making. You are telling other people how you think they should or should not approach decision making.
When statistics is decoupled from decision making, it just means there is a middle man in between. There will not be much of statistical inquiry going on that doesn’t lead to decision making. Nobody would want to fund it if it’s not really used.
“You don’t have to agree with E. J. to appreciate his honesty!”
Meh, I think in the age of the internet hot takes are overrated.
My review of SIST is that it is a very important contribution. Some misc. comments:
-severity is a great example showing that a frequentist/sampling/error statistic approach doesn’t rely only on attained p-values, or only on long-run interpretation
-agree with using a nonparametric treatment to make it more general
-good to deeply discuss Bayes, likelihood, frequentist, etc., approaches where they agree, disagree, interpretations ,etc., and even variations within Bayes and within likelihood and within frequentist schools of thought, ie. philosophy is important
-I agree with the need for coming up with more examples of where severity is useful
-I personally think of severity as doing a sig test (presumably from a well-designed experiment), BUT also doing accompanying calculations using different mus. So you’d get an attained p-value (ie. the original p-value) and the others would be like attained powers, and you’d use the whole set to say what claims (ie. mus) are and are not warranted
(and also maybe use thought experiments using varying xbars)
-I think often it may be more conservative than just going with a significant p-value alone, so as to ‘not make mountains out of molehills’
-a good example is the Water Plant Accident example (https://errorstatistics.com/2018/12/04/first-look-at-n-p-methods-as-severe-tests-water-plant-accident-exhibit-i-from-excursion-3/), basically:
H0: μ ≤ 150
H1: μ > 150
σ = 10
n = 100
observed xbar = 152
What would a standard frequentist treatment be (just p-value?), and how would Bayesians do it?
Justin
http://www.statisticool.com
Following the example in your link, we do a test for mu = 150 with our data x = 152 which gives a low p-value and results in rejection of the null hypothesis.
Can we infer that mu is larger than 153? Obviously not, for that we would need to reject the null hypothesis mu = 153 and the p-value is high when the relevant test is considered.
“You might say, assessing severity is no different from what we would do with a judicious use of existing error probabilities.”
Yes, it doesn’t seem different than a simpler reasoning and straightforward calculation.
“What’s new is the statistical philosophy behind it.”
Ok then.
For what it’s worth, the severities in the tables in that link are just one minus the p-values in the standard frequentist treatment.
Table 3.1 / x = 152
Claim P-value for the corresponding null hypothesis
mu .gt. 149 P(x _gt_ 152; mu = 149) = 0.001
mu .gt. 150 P(x _gt_ 152; mu = 150) = 0.03
mu .gt. 151 P(x _gt_ 152; mu = 151) = 0.16
mu .gt. 152 P(x _gt_ 152; mu = 152) = 0.5
mu .gt. 153 P(x _gt_ 152; mu = 153) = 0.84
Table 3.2 / x = 153
Claim P-value for the corresponding null hypothesis
mu .gt. 149 P(x _gt_ 153; mu = 149) = 0.00003
mu .gt. 150 P(x _gt_ 153; mu = 150) = 0.001
mu .gt. 151 P(x _gt_ 153; mu = 151) = 0.03
mu .gt. 152 P(x _gt_ 153; mu = 152) = 0.16
mu .gt. 153 P(x _gt_ 153; mu = 153) = 0.5
Table 3.3 / x = 151
Claim P-value for the corresponding null hypothesis
mu .lt. 150 P(x _lt_ 151; mu = 150) = 0.84
mu .lt. 150.5 P(x _lt_ 151; mu = 150.5) = 0.7
mu .lt. 151 P(x _lt_ 151; mu = 151) = 0.5
mu .lt. 152 P(x _lt_ 151; mu = 152) = 0.16
mu .lt. 153 P(x _lt_ 151; mu = 153) = 0.03
And
1-p equals chi square df1 of (-2 ln likelihood xbar/likelihood H0). (I.e. Wilks theorem)
Which is ironic because Mayo repudiates the likelihood principle and I think coined the term ‘likelihoodlum’.
Severity is a form of maximum likelihood.
On p. 134 of SIST, she says that “Merely reporting likelihood ratios does not produce meaningful control of errors; nor do likelihood ratios mean the same thing in different contexts.”
so I don’t think she is against likelihood as long as if it is tied back to a sampling distribution and error control,
Justin
http://www.statisticool.com
I think this must be a slip of the pen — in this setting claims aren’t specific values of μ; they’re inferences of the form ‘μ > m’ (or ‘μ m’ for arbitrary values of m could be assessed in this modification of the scenario that turns it into an adaptive design:
H0: μ ≤ 150
H1: μ > 150
σ = 10
one interim look
first look at n = 4, reject null and stop if xbar_4 > 165
final look at n = 100, reject nullif xbar_100 > 152.02 (the +0.02 compensates for additional possibility of Type I error at the first look)
observed xbar_100 = 170
ahahaha I forgot about the html parsing — the mangled looking thing should read: (or ‘μ < m’)
No wait, I lost of lot more of my post than that… okay, what did I write again…? Let’s start over.
I think this must be a slip of the pen — in this setting claims aren’t specific values of μ; they’re inferences of the form ‘μ > m’ (or ‘μ < m’).
Speaking of the water plant accident example, I wonder if you will spend some time thinking about how the severity of the claim ‘μ > m’ for arbitrary values of m could be assessed in this modification of the scenario that turns it into an adaptive design:
[and so on]
#42
To Justin Smith’s comment:
SMITH: I personally think of severity as doing a sig test (presumably from a well-designed experiment), BUT also doing accompanying calculations using different mus. So you’d get an attained p-value (ie. the original p-value) and the others would be like attained powers, and you’d use the whole set to say what claims (ie. mus) are and are not warranted
(and also maybe use thought experiments using varying xbars)
I very much appreciate that you seem to get many of the essential points. But there are a number of things that would need to be cleared up here. Tests, whether of the Fisherian or N-P variety–are reformulated so that the inferences are interpreted according to discrepancies (from a reference test hypothesis) that are well or poorly indicated. Error probs are used to assess and control how well or poorly tested. Inferences are always to be accompanied by corresponding claims that have been poorly tested by the test and data at hand. Neither N-P tests nor p-values give us what’s needed, although one can use the machinery they do provide to obtain SEV assessments. The severity reinterpretation of tests was initially developed building on N-P tests (as a simple way to avoid fallacies of “rejection” and “non-rejection”) as far back as my doctoral dissertation (though I didn’t call it that until around 1990). But I didn’t develop it so much until later (eg Mayo 1996 and 2004/6 with Spanos), as most of my work during those years was on general philosophy of science, not phil stat. The Fisherian construal arose based on work I did with David Cox in 2004-10. Instead of “attained power” (based on NP power), the Fisherian uses the distribution of P over various alternatives, where P is viewed as a statistic. All this is discussed in detail in SIST, as you know (eg Excursion 3 Tour I).
I don’t like the idea of talking about the mus that are warranted because inferences in the severity account take the form of inequalities, e.g., mu ≥ mu’. Nor do I like the idea of changing the null and alternative and using P-values to arrive at SEV computations (although it’s possible). The thing is, P-values need justification and re-interpretation, and that’s one of the things I try to provide. Anyway, we’d need to have more conversations to cover all the necessary ground. Please write to me with queries after this conversation, if you wish.
> Tests, whether of the Fisherian or N-P variety–are reformulated so that the inferences are interpreted according to discrepancies (from a reference test hypothesis) that are well or poorly indicated.
What is the point? You take a test for a null hypothesis mu = mu0 and then use the data (and not just the result of the test) to make inferences relative to other hypothesis (what you call discrepancies) mu1, mu2, etc. In what sense is this approach better than basing inference on the corresponding null hypothesis mu=mu1, mu=mu2, etc.?
A .- Look at that woman next to my brother at the bar. She looks taller than him, and my brother is 6 feet 1. I can’t compare them precisely, because maybe their positions, shoes or haircuts distort my perception, but from here she seems to have two or three inches on him so I’m pretty sure she’s taller.
B .- Oh, you are rejecting the null hypothesis “she’s 6 feet 1”. Can we infer that she’s taller than 7 feet 6 then?
A .- (laughs nervously and changes the subject)
#43
Ungil comments
This would be to commit a “mountains out of molehill” fallacy.
As regards your previous comment, the inference from error statistical tests is not comparative. A comparative inference, as I use that term, takes the form: one hypothesis is better supported, confirmed, is more probable, likely etc. than another. Comparative accounts do not falsify, at least not directly. (To falsify would require the addition of a falsification rule, whose properties then have to be demonstrated.)
The advantage over an NP test, for example, would be to infer, not merely that mu > mu0, say, but to infer claims of form: mu > mu0 + g, for discrepancy parameter g. We at the same time report those discrepancies that are poorly indicated by the data. This is discussed at length in SIST from the very first Excursion.
> This would be to commit a “mountains out of molehill” fallacy.
My point is that there is no fallacy to be dispelled when a five-year-old can see that the question makes no sense. (Ok, I don’t know enough about cognitive development to be sure about five-year-olds, but surely no background in epistemology or other philosophical training is required.)
> The advantage over an NP test, for example, would be to infer, not merely that mu > mu0, say, but to infer claims of form: mu > mu0 + g, for discrepancy parameter g.
Inferring claims of the form mu > mu0 + g for a discrepancy parameter g is equally easy by considering the null hypothesis mu = m0 + g, isn’t it? (I mean from a computational point of view, because from a conceptual point of view the standard approach seems easier to me.)
Say Alice and Bob have the same data and different null hypothesis mu0 and mu0′. If they want to infer claims of the form mu > m0 + g (where mu0 + g = m1) and mu > m0′ + g’ (where mu0′ + g’ = mu1) respectively, we hopefully agree that the same inferences are warranted. I would say that this is a reason to base the inference on the data (which is the same for Alice and Bob) and the claim (which is also the same, mu > mu1), without taking into consideration the original tests which are different but irrelevant.
Wagenmakers seems to think that all who disagree with the general Bayesian approach just don’t want to take the time to study it or deal with the math (rather that conclude a subpopulation has tried it and found it problematic) … because then they would see the light.
I think rather he just demonstrated that one cannot update priors of 0 away from 0, no matter how much data you obtain. This can be interpreted to mean that hard convictions are insensitive to counter-evidence.
Justin
http://www.statisticool.com
#36
To a comment by Just Smith (and also to Wagenmakers, if he will engage)
Yes, and there’s a lot of irony in his stance against the relevance of error probabilities. The following is from SIST 283-4:
“The great irony is that Wagenmakers et al. (2011), keen as they are to show “ Psychologists Must Change the Way They Analyze Their Data” and trade significance tests for Bayes factors, relinquish their strongest grounds for criticism” of p-hackers and data dredgers. While they mention p-hacking has occurred, when it comes to discrediting the inference they put such violations to one side; they are forced to look elsewhere. After all, Wagenmakers looks askance at adjusting for selection effects:
‘P values can only be computed once the sampling plan is fully known and specified in advance. In scientific practice, few people are keenly aware of their intentions, particularly with respect to what to do when the data turn out not to be significant after the first inspection. Still fewer people would adjust their p values on the basis of their intended sampling plan.’ (Wagenmakers 2007, p. 784)
Rather than insist they ought to adjust, Wagenmakers dismisses a concern with
‘hypothetical actions for imaginary data’ (ibid.). To criticize [p-hackers]…Wagenmakers et al. (2011) resort to a default Bayesian prior that makes the null hypothesis comparatively more probable than a chosen alternative (along the lines of Excursion 4, Tour II). Not only does this forfeit their strongest criticism”, they give the p-hacker a cudgel to thwack back at them….
Instead of getting flogged, [the p-hacker] is positioned to point to the flexibility of getting a Bayes factor in favor of the null hypothesis. Rather than showing psychologists should switch, the exchange is a strong argument for why they should stick to error statistical requirements.”
I don’t see why he’s not troubled about this.
Sorry, I meant Justin Smith
EJ could be correct. I speculate that the Bayesian approach in medicine might be questioned.
When you have rejected both Bayesian and fiducial reasoning, what have you got left? … P values. Unfortunately, Mayo even interprets the clear utility of P values poorly. This book gives us a view from the corner in which the author backed herself into a long time ago.
#31
To all who might wish to contribute:
SIST 417-20 discusses several of the answers to a question I once posed on my blog: Can you change your Bayesian prior? The answers are recorded in over 100 comments on my blog. But that’s not my question now.
https://errorstatistics.com/2015/06/18/can-you-change-your-bayesian-prior-i/
The question I would like to ask you all now is this: How do you interpret, or what’s your favored view of, Bayesian probabilities (priors or posteriors)? There seem to be three basic categories: subjectivist, default, or frequentist/ empirical, but there are the multiple meanings given to each. It’s fine to have more than one.
Deborah:
As always, I will take every one of your uses of the term “prior” or “Bayesian probability” and replace it with “statistical model”:
“Can you change your statistical model?”
“How do you interpret, or what’s your favored view of, statistical models?”
Etc.
These issues are real, and they arise in all of statistics (see here), and they’re worth thinking about whether or not you use Bayesian methods.
True priors are models, but they seem different. Since:
-likelihood can swamp priors
-priors are supposed to be pre-data
-priors are probability distributions put on parameters
-priors not as agreed upon as likelihood models
-branch of Bayesian exists called ‘subjective’ and priors are tied to this
Justin
http://www.statisticool.com
By the way, if you follow de Finetti, all probability assessments before observing/analysing data are the “prior”, which has a predictive interpretation for the not yet observed data. In his account the term (and idea) of priors is not restricted in any way to a “distribution on parameters”. De Finetti’s theorem only shows that under exchangability the whole prior (what he calls prior) can be decomposed into “parameter prior” (which is what is called “prior” by most), and the likelihood given the parameter. This is a helpful technical result, but doesn’t, in his view, give the parameter any meaning on its own (although he wouldn’t deny that there are situations in which the meaning of the whole setup and prior relies on the interpretation of the parameter).
Re: my original comment of ‘priors seem different’, I’d also add things like:
“Why optional stopping is a problem for Bayesians” by Heide and Grunwald (https://arxiv.org/pdf/1708.08278)
Justin
http://www.statisticool.com
#35
To Gelman
Well the model is generally thought to describe an aspect of the data generating mechanism, cashed out in a frequentist sense. This might be a meaning of prior, at least when there’s a theta generating mechanism, but it’s clearly not the only one, and I appreciate your paying a lot of attention in your work to the different definitions.
You don’t run priors and likelihood together when you say things like “Bayesians Want Everybody Else to be Non-Bayesian.” in (Gelman 2012, p. 53) :
“Bayesian inference proceeds by taking the likelihoods from different data sources
and then combining them with a prior (or, more generally, a hierarchical model).
The likelihood is key. . . . No funny stuff, no posterior distributions, just the
likelihood. . . I don’t want everybody coming to me with their posterior
distribution – I’d just have to divide away their prior distributions before
getting to my own analysis. (ibid., p. 54)”
You are clearly giving a different treatment to priors and likelihoods, and recommending they be distinguished in analyzing an inquiry.
The truth is we don’t want likelihoods either, what we want is raw data. there are much bigger disagreements about generating processes than there are about priors.
Daniel:
+1 on that. I was being sloppy in my earlier writing on the topic which Mayo quoted.
#32
To all, especially those who follow Gelman’s approach.
One of the things I like about Gelman’s approach is the importance he places on testing underlying statistical models. He’s critical of Bayesians (and others) who don’t test their models (including any priors). He would consider a model resulting from his data-analysis cycle better tested and thus better at solving its problems than untested or poorly tested models–and rightly so. But I take it Gelman wouldn’t translate a claim about a model’s being well-tested into assigning it a probability.
“I do not trust ‘Bayesian induction over the space of models because the posterior probability of a continuous-parameter model depends crucially on untestable aspects of its prior distribution” (Gelman 2011, p. 70).
Yet there’s still a need to qualify the resulting model in some way. How? On SIST (p. 305) I suggest that
“for Gelman, the priors/posteriors arise as an interim predictive device to draw out and test implications of a model. What is the status of the inference to the adequacy of the model? If neither probabilified nor Bayes ratioed, it can at least be well or poorly tested. In fact, he says, ‘This view corresponds closely to the error-statistics idea of Mayo (1996)’ (ibid., p. 70)”.
The error statistical account I favor (based on quantifying and controlling well-testedness) supplies a way to qualify uncertain inferences that is neither a “probabilism” (posterior, Bayes Factor or Likelihood Ratio) nor an appeal merely to a method’s (long-run) performance. The severe testing account may supply the form of warrant in sync with Gelman’s approach (a measure of how well probed). If not, how are the resulting models to be qualified?
As Gelman tells us in this post “I would not quite say that statistical inference is severe testing, but I do think that severe testing is a crucial part of statistics.” We need ways to assess how severely claims (of various types) are warranted, and that’s what the severe testing account develops.
Can you apply severity testing to the example Robert Cousin’s brought up, that I looked at here:
https://statmodeling.stat.columbia.edu/2019/04/12/several-reviews-of-deborah-mayos-new-book-statistical-inference-as-severe-testing-how-to-get-beyond-the-statistics-wars/#comment-1014345
I think what most people want is just a real life example of how your idea should be applied, not more paragraphs.
Dear all
This comment is about p-values and Wikipedia. Which, like it or not, is nowadays just about anyone’s “first port of call” if they hear that these things exist , for instance if they hear that there is some kind of controversy going on about them. Here’s the URL for those who want to check *really* fast themselves: https://en.wikipedia.org/wiki/P-value . *Warning*: anyone may edit just about any wikipedia article at any time. Fortunately, all edit history is preserved and anyone, at any time, can revert to an earlier version. [Unless someone with wikipedia super-powers steps in].
By the way, I didn’t read Deborah’s book yet. I do want both to read her book and the discussion here in the near future, but as they say, the way to hell is paved with good intentions, and life is short. And – I’m a mathematical statistician with an inclination to frequentism and a love of controversy.
I do care about p-values: they are there and will be there for some time to come; they are abused; therefore it’s important, I think, that people at least have a good chance of finding out what they actually are. Recently I was discussing them with a mathematician friend who comes from a very, very different part of mathematics from me, and though she had often heard talk of p-values, and had even written something about their abuse, she did not really know what they were. I suggested we hold a Socratic discussion on the subject and asked her first to try to formulate a verbal definition. I gave her permission to consult the usual oracle on this – Google.
She rapidly found (English) Wikipedia and couldn’t make head or tail of the leading sentence. Even though it looks pretty much like a respectable internet encyclopedia definition. I took a look at it and found out it was (a) dangerously ambiguous, (b) self-contradictory, (c) wrong.
I’m talking about *one* sentence.
Knowing the ingrained habits of present-day students and being an enthusiastic wikipedian, I edited it myself immediately. [My changes were minute – I moved a comma or two, exchanged a couple of phrases, and added “absolute value of” where it was absolutely needed, in order at least to correct the three distinct errors which I had found]. I expected an instant edit war to break out, but it didn’t. So far there has been a deafening silence. I still have to round off my own editing – my modified text goes together with the literature references belonging to the former version of the text. I guess no-one cares about p-values and the education of the young anymore. Maybe they just have other things on their mind [as I write this, Notre Dame is still smouldering. I haven’t checked wikipedia this morning, yet].
I mentioned all this on Facebook. Another mathematician friend came up with a mathematical definition which was a beauty. Of course, that doesn’t belong in Wikipedia, but if some discussion does start up here or on the wikipedia p-value “talk pages”, I will share it with the world.
Yours
Richard Gill
emeritus professor of mathematical statistics, University of Leiden, Netherlands.
Thanks for bringing this up. I glanced at the Wikipedia page you linked, and agree that is is not a good source for most people to use to understand what a p-value is. As another example from that page, the first sentence from the section Basic Concepts reads:
“In statistics, every conjecture concerning the unknown distribution F of a random variable X is called a statistical hypothesis. ”
I would guess that many people wanting to know what a p-value is would not understand any of the terms “conjecture”, “distribution”, or “random variable”.
My own attempts to explain p-values, etc. to people who encounter them in their work but do not have a strong statistical or mathematical background resulted in some lecture notes that are at
https://web.ma.utexas.edu/users/mks/CommonMistakes2016/commonmistakeshome2016.html.
These are far from perfect, but at least try to avoid the extremes of overly technical or overly simplified.
Dear Martha
I enjoyed hunting through your slides for the definition of p-value, and I enjoyed what I found.
I think there is serious omission. What if the null hypothesis is composite????
This was also a mistake in the wikipedia definition.
I do consider it a serious mistake since almost all routine p-value computations do in fact involve a composite null hypothesis.
Richard
The definition should be the same as long as you recognize the thing being tested is the entire null model rather than a single parameter value. The “composite” model is different so the p-value will be different, but still has the same meaning.
Very true, but you need to start somewhere and almost everyone starts out with a simple NULL of usually zero effect.
Now as all routine p-value computations do in fact involve a composite null hypothesis (e.g. two group randomized trial with binary outcomes) how and when to proceed is a critical topic. You will see a lot of discussion here regarding whether strong severity itself has been sufficiently worked up into realistic routine problems and who should do that.
As for composite null hypotheses (as you likely know better than me) many prefer taking the supremum where as I prefer to treat the p-value as a function over the composite null hypothesis, using graphs to clearly display this (easy now given fast simulation).
(Interestingly, even some statisticians are surprised by such graphs.)
Richard said,
“I think there is serious omission. What if the null hypothesis is composite????
This was also a mistake in the wikipedia definition.
I do consider it a serious mistake since almost all routine p-value computations do in fact involve a composite null hypothesis.”
As I wrote above, “These are far from perfect, but at least try to avoid the extremes of overly technical or overly simplified.” Getting into composite hypotheses would (sadly) be overly technical for all but a very few of the people (“people who encounter [p-values, etc.] in their work but do not have a strong statistical or mathematical background”) in the continuing education course for which the notes were used. For this audience, in the time-frame involved, the aim was to try to get them to develop a healthy skepticism of claims based on p-values, and perhaps to give them a better background to begin to learn more.
Long before Mayo, Popper, or even Pierce, it was standard to subject hypothesis to hard tests — to put them “through the ringer” as it where — before giving them much credence. It wasn’t until Frequentist statistical methods came along before entire fields believed there was different way to do things.
So all of this is trying to correct a problem frequentist statistical philosophy and practice created. Mayo’s verbal exhortations to put hypothesis to hard tests doesn’t add or fix a thing. The only hope for a contribution is her implementation of those ideas in her severity function (SEV).
Unfortunately Mayo’s seemingly never made a statistical inference in her life and appears to lack the technical background to do so. SEV was only ever tested in the most simple of instances where it (and any other reasonable answer) gives the same result as Bayes. No one can seemingly find any instance where they disagree where Bayes isn’t clearly right.
Mayo and her fellow frequentist apologists staunchly refuse to put Mayo’s ideas to even the mildest of hardships, let alone a severe test. Apparently simply agreeing with Mayo’s fanatical anti-baysian philosophy is all the proof anyone needs.
In 2019 this in is considered a valuable contribution to statistics.
Anon:
Unfortunately, it’s been my impression for decades that many developers and users of statistics really don’t want to put their assumptions to the test, and that statistical methods often seemed to be developed and used specifically to avoid putting cherished assumptions at risk.
We know all about this in classical statistics, with “p less than 0.05” taken as a statement that an effect is real, and with “p less than 0.05 & publication in a top journal” taken as a signal that we’re not supposed to criticize a claim, however implausible it is from the standpoint of science. And, conversely, when “p more than 0.10” is taken as a statement that an effect is zero or unimportant. Or, even more ridiculously, when “p in between 0.05 and 0.10” is taken as a statement that an effect is small. Indeed, null hypothesis significance testing is rarely about severe testing of models; it’s usually the opposite: a way to manufacture confident statements and avoid severe testing.
But similar problems arise in Bayesian statistics: I’ve seen lots and lots of Bayesians—including various eminent researchers back when I attended a Bayesian conference back in 1991—who held the position that Bayesian models didn’t need to be checked, indeed shouldn’t be checked, because they were “subjective.” This always seemed to me like a bizarre position to take—if an assumption is subjective, shouldn’t we be under more obligation to check it?—but there you have it. Not putting assumptions to the test: not just a way of life, also a fundamental principle.
Regarding Mayo’s book: I would not call it a “contribution to statistics,” but that’s fine—it’s not a statistics book, it’s a philosophy book. What I do think is that statistical philosophy and statistical practice have serious gaps, and I’m glad that Mayo and others are thinking about these issues, even if they sometimes or even often express ideas that I think are mistaken.
#49
to Gelman’s comment
My book is a contribution, not to “philosophy,” but to “statistical philosophy” and, as you yourself say above, “good philosophy can facilitate both the development and acceptance of better methods”. Among the wide-ranging audience for whom my book is intended (see ”Who is the Reader of This Book”, p. xiii), my book is for statistical practitioners who want to develop the logical skills to independently scrutinize: the meaning and assumptions of their statistical inferences, how we arrived at today’s statistics wars, the arguments put forward for why one method is to be preferred to another, and the various statistical “reforms” put forward by leaders in statistics. As I say on p. 12, these tasks require “a dose of chutzpah that is out of the ordinary in professional discussions” (p. 12).
But let me now see if you will answer the question I put forward to readers in my comment #32, be it regarded as a statistical or philosophical question. Here’s the main part:
#32
To all, especially those who follow Gelman’s approach.
On SIST (p. 305) I suggest that
“for Gelman, the priors/posteriors arise as an interim predictive device to draw out and test implications of a model. What is the status of the inference to the adequacy of the model? If neither probabilified nor Bayes ratioed, it can at least be well or poorly tested. In fact, he says, ‘This view corresponds closely to the error-statistics idea of Mayo (1996)’ (ibid., p. 70)”.
The error statistical account I favor (based on quantifying and controlling well-testedness) supplies a way to qualify uncertain inferences that is neither a “probabilism” (posterior, Bayes Factor or Likelihood Ratio) nor an appeal merely to a method’s (long-run) performance. The severe testing account may supply the form of warrant in sync with Gelman’s approach (a measure of how well probed).
Yes?
Anon, her “On the Birnbaum Argument for the Strong Likelihood Principle” in Statistical Science (https://projecteuclid.org/download/pdfview_1/euclid.ss/1408368573) seems pretty technical IMO.
Re: “It wasn’t until Frequentist statistical methods came along before entire fields believed there was different way to do things.”
By different you must mean better, since subjective Bayes approach allows for literally any prior to be used, possibly brittle ones that vary from person to person, even improper, modelling beliefs. Not to mention, experimental design, sampling theory, and quality control revolutionized science and the world. If I search PubMed for “p <" it shows many millions of hits, but "Bayesian" or "Bayes factor" not even over 50,000 hits. People are pretty practical, and I'd expect if Bayes is "clearly right" then practice would reflect this, but it doesn't seem to unless I've missed something.
Here are a few examples of people not "agreeing with Mayo" but coming to their perspective from logic and evidence and issues with other approaches:
-"Why I am Not a Likelihoodist", by Gandenberger (https://quod.lib.umich.edu/cgi/p/pod/dod-idx/why-i-am-not-a-likelihoodist.pdf?c=phimp;idno=3521354.0016.007;format=pdf)
-"In Praise of the Null Hypothesis Statistical Test" (https://pdfs.semanticscholar.org/37dd/76dbae63b56ad9ccc50ecc2c6f64ff244738.pdf), by Hagen
-"Will the ASA’s Efforts to Improve Statistical Practice be Successful? Some Evidence to the Contrary" (https://www.tandfonline.com/doi/full/10.1080/00031305.2018.1497540), by Hubbard
-"The practical alternative to the p-value is the correctly used p-value" (https://psyarxiv.com/shm8v), by Lakens
-"So you banned p-values, how’s that working out for you?" (http://daniellakens.blogspot.com/2016/02/so-you-banned-p-values-hows-that.html), by Lakens
-"Assessing the Statistical Analyses Used in Basic and Applied Social Psychology After Their p-Value Ban" (https://www.tandfonline.com/doi/abs/10.1080/00031305.2018.1537892), by Ricker et al
-"On the Brittleness of Bayesian Inference" (https://epubs.siam.org/doi/pdf/10.1137/130938633), by Owhadi et al
-"Bayesianism and Causality, or, Why I am Only a Half-Bayesian" (http://ftp.cs.ucla.edu/pub/stat_ser/r284-reprint.pdf), by Pearl
-"Why Isn't Everyone a Bayesian?" (http://www2.stat.duke.edu/courses/Spring07/sta122/Readings/EfronWhyEveryone.pdf), by Efron
-"The case for frequentism in clinical trials", Whitehead
-"Legal Sufficiency of Statistical Evidence" (https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3238793), by Gelbach et al
-"Bayesian Just-So Stories in Psychology and Neuroscience" (http://psy2.ucsd.edu/~mckenzie/Bowers&Davis2012PsychBull.pdf), by Bowers et al
-"Why optional stopping is a problem for Bayesians" (https://arxiv.org/pdf/1708.08278), by Heide et al
-"In defense of P values" (https://pdfs.semanticscholar.org/1751/17f8f60e422c9e78f9766f39a2812c564e46.pdf), by Murtaugh
-"A Systematic Review of Bayesian Articles in Psychology: The Last 25 Years" (http://psycnet.apa.org/fulltext/2017-24635-002.html), by van de Schoot et al
-"On Using Bayesian Methods to Address Small Sample Problems" (https://www.tandfonline.com/doi/abs/10.1080/10705511.2016.1186549?journalCode=hsem20), by McNeish
-empirical laws, for lack of better word, of the Strong Law of Large Numbers, the quincunx making a normal distribution, and likelihood swamping priors.
Cheers,
Justin
http://www.statisticool.com
No amount of collecting citations favourable to your views can replace engaging with the strongest arguments against them. So while I thank you for this nice collection of links for me to read, I have to wonder if you’re submitting your commitment to frequentist methods to the severest possible test.
Hmm, I thought I was responding to Anonymous. I guess my prior was brittle.
Justin
http://www.statisticool.com
Bit of a free-for-all in these here comment threads. My guess is that if this particular Anonymous (who is not anonymous to me or, likely, to other long time denizens) chooses to reply he’ll probably not engage you on the substance of your links as he will see none. (Brittle is old old news by now…)
HAPPY BIRTHDAY JERZY NEYMAN!
https://errorstatistics.com/2019/04/16/a-spanos-jerzy-neyman-and-his-enduring-legacy-4/
#45
To a comment by Corey (there’s no room to reply immediately below)
https://statmodeling.stat.columbia.edu/2019/04/12/several-reviews-of-deborah-mayos-new-book-statistical-inference-as-severe-testing-how-to-get-beyond-the-statistics-wars/#comment-1016560
The severe tester observes, first of all, that succeeding with (a) the job of blocking BENT cases is the converse of succeeding with (b) the job of declaring “well-tested” all non-BENT cases, and the latter is still different from declaring “well-tested” all “obviously correct” claims. Second of all, even though you’re not talking about the first (a)–the most important direction for the severe tester–, it’s worth noting that she does not claim that error probabilities are adequate to block all BENT cases, if they were, there would have been little need for the (meta-statistical) notion of severity. In other words you can have great error statistical performance for a method that yields a terribly tested hypothesis, as I explain in the very first Tour. Looking up chestnuts and howlers would produce particular examples. Performance differs from probativism.
As for the converse (b), the one you claim to be worried about, the severe tester likewise says that an inference C may be arrived at by a method with bad error probabilities, while C is known to be true. Even a terrible method can get lucky. (After all, even astrological predictions can sometimes be right on the money!) Good error probabilities are neither necessary nor sufficient for a claim to be warranted. We may have other information about C’s “obvious correcness”. There are many cases where we’d want to say C is true but terribly tested by this particular method! C’s truth or probable truth isn’t the same as C’s being well tested.
But now let’s suppose you have an example of a method and you can show C has been put to and passes a highly severe test by dint of that method. (As you know, C has passed a severe test if it has been subjected to, and passes, a test that very probably would have found specified flaws in C, if they are present.) Presumably Corey’s computation of C’s well-testedness can be computed by others as well. Therefore it can be computed by the severe tester as well. Thus, she can agree that C has passed severely, if indeed it has.
This is the sort of happy talk that sounds plausible but fails to actually get down to brass tacks. I will take it as an invitation to give you the first step — only the first step, not the complete argument — and see if you can come this far with me.
The setting is a toy model of an early stopping trial. The model is a normal distribution, mean μ, variance 1. We aim to test H0: μ ≤ 0 vs. H1: μ > 0. The test statistic is the observed mean. The maximum sample size is n = 2 with an interim look at n = 1. We reject the null on the 1st look and stop if the observed mean is greater than 2.0. We reject the null on the 2nd look if the observed mean is greater than 1.125. This gives the design a Type I error rate of 0.05.
Consider four possible outcome scenarios:
1, weak. Barely reject on the 1st look, observed mean = 2.001
1, strong. Deep in the reject region on the 1st look, observed mean = 3.0
2, weak. Barely reject on the 2nd look, observed mean = 1.126
2, strong. Deep in the reject region on the 2nd look, observed mean = 1.8
We want to know what discrepancies from the null are well or poorly supported in these scenarios. It seems clear they should give rise to different SEV functions: the strong scenarios should yield evidence for larger discrepancies from the null than the corresponding weak scenarios; and the 2nd look scenarios, being based on more data, should induce steeper SEV functions than the corresponding 1st look scenarios.
From your severity criteria we know that the inference ‘μ > m’ passes a severe test if with very high probability the test would have produced a result that accords less well with ‘μ > m’ than the actual data, if ‘μ > m’ were false or incorrect. If So we know that
SEV(μ > m) = Pr( some event ; μ ≤ m)
How can we tell, in each of the above four scenarios, what is the set of results that accord less well with ‘μ > m’ than the observed mean and sample size? In the 1st look scenarios, what part (if any) of the 2nd look sample space belongs in that set, and vice versa?
In the past you have directed me to the relevant literature on the general topic of such designs, but all of that is focused on how to achieve desired Type I error rates, how to monitor them as they proceed, and how to calculate p-values and confidence intervals at the end. Nowhere is the proper construction of SEV addressed (nor could one reasonably expect it to be).
That’s a very good question. I’m looking forward to seeing the answer (although my sujective prior for getting one is quite low).
“Presumably Corey’s computation of C’s well-testedness can be computed by others as well. Therefore it can be computed by the severe tester as well.”
I should say why this argument, seemingly so ironclad, goes wrong. It’s assumed a false premise, to wit, that I am relying on some non-SEV computation of C’s well-testedness. In my argument C’s obvious correctness arises because we have a consistent estimator with the usual 1/sqrt(n) rate and an unbounded amount of data.
#46
To Corey
I don’t assume it is non-SEV, whatever that means. If there’s a SEV computation (or even a recognition through other means) of C’s well-testedness, then the severe tester can use it too.
Mayo, if you can’t answer the very specific question I asked about what event we should be basing the SEV calculation on then just say so.
But anyway, here’s why you’re wrong. Criterion (S-2) is pretty specific about what kind of event we ought to be looking at: tail areas. But unlike in the fixed sample size design, the notion of a tail area is ambiguous in designs with interim looks — if it weren’t, you would be able to answer my question. The adaptive design literature describes a few different ways of defining tail areas for the purpose of calculating p-values. It turns out that all of those candidate definitions of the notion of a tail area produce SEV functions that are certifiable garbage. In what sense are they garbage? To understand that, one actually has to be able to do the math, or at least follow along.
A severe tester who affirms that none of the candidate SEV functions that I call garbage are “true” measures of severity then has to either (i) admit that the Error Statistics paper’s arguments that depend on the existence of the SEV function (items #2, #3, #6, and possibly #4) do not apply to adaptive designs, or (ii) construct a SEV function that is worthy of the name, perhaps by recognizing and fixing criterion (S-2)’s deficiencies.
The point is: you have work to do.
> If there’s a SEV computation … then the severe tester can use it too.
So if it works – it will work for anyone who knows that it works, how and what to make of it ;-)
Every one should be interested in which of the assumptions they are using that are too wrong in this particular study. So being aware of how likely you might be of becoming aware of the whats wrong should be helpful as long as the assessment of that is not too uncertain or even worse is taken as being as too certain. Even if it is severity all the way down, it can’t be just ignored.
To me – the the assessment of that is based on identifying the least wrong reference set and what would happen repeatedly in an inexhaustible collection from that reference set.
I am a practicing physician who has found the concept of severe testing discussed by Deborah Mayo in her marvelous book SIST to be immensely helpful in understanding how statistical inference of a disease from data in a patient is done in practice. This inference is not Bayesian as we see clearly in all diagnostic exercises in real patients which are published regularly in The New England Journal of Medicine. Diagnosis in these exercises are performed by highly experienced, academic physicians who are surely familiar with the Bayesian method. In all of them, a disease suspected from symptoms is formulated as a diagnostic hypothesis regardless of its prior probability and inferred conclusively from result of a severe test which usually has a likelihood ratio greater than 10.This method is highly accurate leading to a diagnostic accuracy of greater than 95 percent in these exercises. I am not certain but this looks like a frequentist confidence method of inference to me.
It is of interest the Bayesian method has been prescribed for statistical inference in diagnosis on grounds of its rationality in terms of winning a bet with it since the early 1960s.The amazing thing to me is that the inferential accuracy of this method in practice has never been studied perhaps because as Andrew Gelman mentions in one of his posts that this method is subjective and its accuracy cannot be studied.
It would be extremely useful, I think,if statisticians studied how statistical inference is actually performed in practice in a field like diagnosis. Then as far as I am concerned, the method that is actually employed is the correct method regardless of any theoretical considerations such as rationality etc.
I think statistical inference in diagnosis in practice has not been studied so far as it is a borderline problem falling on the borders of medicine and statistics whose respective practitioners have different backgrounds and training. But the value of such study would be immense as it may improve inferential accuracy in diagnosis.
a lot of what I think are misapprehensions here to unpack. first the assumption that academic physicians understand Bayesian inference. most probably don’t. next that likelihood ratios are frequentist tests involving severity… I’ve tried to ask Mayo about this above and she doesn’t respond. in general she seems extremely down on likelihood approaches. finally that diagnostic accuracy is itself meaningful. what matters isn’t how often when you meet the criteria you get the diagnosis correct but rather what is the typical outcome quality. how many people go untreated because they don’t meet the diagnostic criteria, but they do in fact have the disease for example.
#47
Bimal Jain MD comment:
“I am a practicing physician who has found the concept of severe testing discussed by Deborah Mayo in her marvelous book SIST to be immensely helpful in understanding how statistical inference of a disease from data in a patient is done in practice.” Thank you for expressing appreciation.
Just checked the famous ASA definition of the beloved p-value. It seems that nobody realises it is explicitly *informal*. Moreover it seems that nobody realises it is limited to the case of a simple null hypothesis. The limitation is nowhere mentioned in that publication, as far as I can see. Most applications of p-values have a composite null hypothesis. eg one-sided one sample Z-test, composite null hypothesis, composite alternative hypothesis
This has repercussions all over the place, for instance to Wikipedia, and from there, to the whole world…
Our comments missed each other https://statmodeling.stat.columbia.edu/2019/04/12/several-reviews-of-deborah-mayos-new-book-statistical-inference-as-severe-testing-how-to-get-beyond-the-statistics-wars/#comment-1019437
I agree its important but not that it has to be done in the very first step.
Write out the equations for how to calculate a p-value for the two models, they will be different. The p-value will still be the probability of seeing at least as extreme a deviation from the prediction of the model.
#48
Comment by Gill.
Many of us have noticed the fact that the ASA doc keeps to the point nil null, despite the fact that one-sided tests are generally more apt. It’s easier to knock down the stilted significance test with a nil null–the same artificial variation on tests that we see in the 2019 article (warning us not to use the words “significant/significance”). Moreover, there is no indication of the requirements for a Fisherian test statistic (as I delineate in SIST). The document does mention that for simplicity it is leaving out a consideration of power. Nearly all the examples you see showing disagreement between the p-value and other measures (posteriors, Bayes factors) use a spike prior on the nil null. One of the more popular alternatives to p-values, J. Berger’s BFs, doesn’t work for one-sided tests–as we checked the other day when he was here. It’s too bad you weren’t in on writing the document.
Mayo wrote in response to my comments coming from the trenches: “I’ve no doubt there are wider topics than the stat wars, but it’s pretty wide wouldn’t you say? I’ll look for your book on info quality.”
Pretty wide,…..pretty wide,………….pretty wide !!!!!
Yes, statistics is (should be) pretty wide. Please try to move away from the comfort zone and embrace a wide perspective.
For example:
Regarding the combination of frequentist-Bayesian views, see “Sampling and Bayes’ Inference in Scientific Modeling and Robustness”, by G. Box”, Journal of the Royal Statistical Society, Series A, Vol. 143, No. 4, pp. 421-422, 1980 – this is pretty wide.
Regarding how to view the role of statistics from a wide perspective, see my Hunter conference paper “Statistics: A Life Cycle View” Quality Engineering (with discussion), Vol. 27, No.1, pp. 111-129, 2015.
Regarding what should be the main thrust of statistics, generating information quality: “On Information Quality” (with G. Shmueli), Journal of the Royal Statistical Society, Series A (with discussion), Vol. 177, No. 1, pp. 3-38, 2014.
To me it seems essential that we take a pretty wide perspective….
As a follow up to my last comment in this great sequence of discussions, and if you are interested in the future of statistics you will greatly benefit from the dean;s lectur of Roger Peng: https://www.youtube.com/watch?v=qFtJaq4TlqE&feature=youtu.be
I’ve been reading the book, and when I came back to this thread with a little more context, I noticed that something I had posted was evidently lost in moderation.
My original post was a link to the NY Times web app where you are instructed to determine the pattern behind a series of numbers. You are allowed to repeatedly probe the algorithm by entering your own number series and the app will return whether your series follows the hidden pattern or not. When you’re finally satisfied that you have figured the rule out, you enter your final answer. It turns out that a huge percentage (~80% I think?) of those taking the test submitted their answer without once inputting a series that received a “No” answer. That is, the vast majority of participants were willing to submit an answer which they never actually challenged! They confirmed their initial guess until they got bored and then went with it.
I think this is they key to statistics, data science, machine learning, economics, physics, et al, and to the extent that Mayo’s book explores the statistical techniques that support this “vigorously beat up my model and see if it still stands” approach — i.e. the scientific method — it’s a gem. The book is a well-written survey that shows her knowledge and thinking is broad and deep. At the same time, I feel like the thesis that she might have printed out and hung on the wall as she was writing is something like: a) scientists should be rigorous, and b) frequentism, properly understood and rigorous, was right all along and Bayesians are wrong; any so-called wars were simply various misunderstandings of frequentism.
Andrew, as he’s noted in this thread, is taken seriously, but it feels like his ideas are more of a foil for completing her criticism of Bayesian inference Cat-in-the-Hat-style, with Andrew being the final Bayesian cat that refutes the prior Bayesian cat that refutes the prior Bayesian cat… but then she seems to dismiss Andrew’s ideas as either too tentative and incomplete to be useful or as a Bayesian veneer over frequentism.
Very late to this party, but let me add a couple of cents of mine to the discussion. Trying to keep this review relatively short, I should preface it by saying that I found SIST to be a very mixed bag of some welcome passages pointing out some context, especially in Fisher and Popper, that is usually ignored. Unfortunately, that is completely undermined by Mayo’s all-out inductivism—or, to give it its full name, “the whole discredited farrago of inductivism” (Medawar).
Mayo’s launching-off point for SIST is this question: “How do humans learn about the world despite threats of error due to incomplete and variable data?” (SIST, xi) Her answer, in short, is: by severely testing our claims. This is, at least in part, based on the philosophy of Karl Popper, arguably the 20th century’s most important philosopher of science: “The term ‘severity’ is Popper’s, though he never adequately defined it.” (SIST, 9) Mayo proposes that she has actually found a previously missing adequate definition, and it is this: “If [a claim] C passes a test that was highly capable of finding flaws or discrepancies from C, and yet none or few are found, then the passing result, x, is evidence for C.” (SIST, 14) This Mayo does not want to be misunderstood as saying that, using this method, we find true or even probable statements: “I say inference C may be detached as indicated or warranted, having passed a severe test” (SIST, 65). And this, per Mayo, is explicitly an example of “ampliative or inductive reasoning” (SIST, 64), for which a variety of statistical methods (depending on context) can be used.
About those statistical methods, it is to Mayo’s credit that she stresses, right out of the gate, that one of the most pernicious uses of statistical methods had been anticipated and explicitly denounced by Fisher himself as early as 1935: “Fisher…denied that an isolated statistically significant result counts” (SIST, 4), going on to quote him saying that “[i]n relation to the test of significance” we need to “know how to conduct an experiment which will rarely fail to give us a statistically significant result”. That admonishment alone should have been enough, one would have thought, to preclude basing any far-reaching conclusions on a single study’s outcome (e.g. its p-value), such as “claiming a discovery”.
Similarly, it is very welcome for Mayo to point out (SIST, 82-3) that Popperian falsification is not achieved by noting one observation that contradicts a theory but only with the help of something that Popper called a “falsifying hypothesis”. It would have been helpful, however, to actually quote the relevant passage from Popper’s Logic of Scientific Discovery, as Mayo (partially) did in her earlier book (EGEK, 14):
All well and good. But then, unfortunately, Mayo’s train of argument veers dangerously off course, eventually missing its intended target completely. One would certainly have to concur with her when she says, “The disagreements often grow out of hidden assumptions about the nature of scientific inference”. In Mayo’s case, at least, the assumptions aren’t all hidden. She is brazenly upfront about championing induction, for a start. “In getting new knowledge, in ampliative or inductive reasoning, the conclusion should go beyond the premises” (SIST, 64), she claims, and: “Statistical inference goes beyond the data – by definition that makes it an inductive inference.” (SIST, 7-8) Now, she is perfectly aware that induction has a bit of a problem: “It’s invalid, as is so for any inductive argument.” (SIST, 61) But that isn’t a problem, according to Mayo, on the contrary: “We must have strictly deductively invalid args to learn” (Twitter). Indeed, Mayo has confirmed in a separate conversation that she is “not talking of a logic of induction”. What, then, is she talking about when she talks about “inductive inference”? The answer: “error probabilities”, in line with her definition of severe tests. In fact, Mayo thinks that Popper foundered because “he never made the error probability turn” (SIST, 73).
One other assumption, however, is a little removed from plain view. This is Mayo’s assumption about the aim of science. This remains surprisingly vague, with “craving truth” (SIST, 7), “learn[ing] about the world” (xi), “getting new knowledge” (64), and “distinguish[ing] approximately correct and incorrect interpretations of data” (80) being our only hints as to what, in Mayo’s view, it is all about. Even more surprisingly for a professional philosopher, she never defines, or otherwise talks about, the terms ‘truth’, ‘learning’, and ‘knowledge’, as if they were self-explanatory and everybody was in agreement about their meaning—which they emphatically aren’t and obviously everybody isn’t. Other crucial terms, such as ‘inference’ and ‘hypothesis’, fare only a little better, getting a casually hand-wavy one-sentence definition each.
Not quite incidentally, these terms, and the concepts behind them, are crucial to any understanding of the philosophy of science—and especially Popper’s version of it. For all her professed sympathy for Popper’s philosophy, Mayo unfortunately either misunderstands or flat-out ignores some of the most central concepts in Popper’s philosophy. These, in fact, turn out to be the keys to a solution to the current crisis in the social sciences.
(continued below)
(cont.)
It all starts with Mayo’s ill-considered faith in induction. Popper emphatically denied that there was any kind of induction—not just that as a logical process it was invalid but also that any kind of inductive reasoning was used either for theory formation or in the production of knowledge. Mayo variously claims that Popper only rejected “enumerative induction”, that corroboration via falsifying hypotheses necessitates “an evidence-transcending (inductive) statistical inference” (SIST, 83), and even (without, I should add, being able to provide any evidence) that Popper actually “doesn’t object” to calling such an inference ‘inductive’—claims that range from the wildly mistaken to the outright preposterous. Compare, for example, Popper’s treatment of Baconian induction, which goes far beyond the enumerative kind (Logic, passim and 438); his footnote in § 22 of Logic explaining the concept of a ‘falsifying hypothesis’; and this almost derisive put-down: “It is clear that, if one uses the word ‘induction’ widely and vaguely enough, any tentative acceptance of the result of any investigation can be called ‘induction’.” This last reply could just as well have been directed at Mayo, who certainly uses ‘induction’ vaguely enough to warrant it.
Just as weirdly, Mayo seems to be unaware that Popper had a subtly but completely different aim in mind with respect to science. For her, it is about how “humans learn about the world” and how we “get new knowledge”. For him, the “central problem” is “the problem of the growth of knowledge” (Logic, Preface 1959). Popper’s aim is not to find new knowledge but ever better knowledge; the difference should be obvious after a moment’s thought: “new knowledge” doesn’t even so much as imply any coherence, let alone improvement. Popper understood very well that it’s impossible to judge whether a theory is per se near or far from some absolute truth; that’s why everything in his methodology is about making it possible to judge whether some theory is at least better than some other(s). Popper’s view—entirely correct, in my estimation—is that induction is not just useless, it is not even needed.
When she dismisses deductive logic, Mayo not-so-subtly shifts the goalposts from a critic’s observation that induction is not even valid to some variation of, ‘Oh but then deductive arguments don’t ensure soundness’ (i.e. truth). Well, that’s actually not what any argument does. What logic can do (iff we accept the principle of non-contradiction) is to let us force ourselves to make a choice—in the logician Mark Notturno’s phrase: “No argument can force us to accept the truth of any belief. But a valid deductive argument can force us to choose between the truth of its conclusion on the one hand and the falsity of its premises on the other.” In a methodology that is about deciding which of two ideas is better, that is in fact all you need; again, Notturno:
Consequently, Mayo is similarly off the mark when she thinks science is about marking out “approximately correct” ideas (SIST, 80). By what standard? We don’t know, because Mayo didn’t bother to say what she takes ‘truth’ to mean. She also doesn’t mention that Popper had a different idea. In Notturno’s words: “The primary task of science is not to differentiate the true from the false—it is to solve scientific problems.” For Popper, scientific theories (and hypotheses, which are substantially the same thing) are about explanation; if there is no explanatory theory, there are no hypotheses and there is no knowledge. Mayo effectively turns all that completely on its head (EGEK, 11-2):
In this way, she empties all relevant terms of any possibly helpful meaning. “Inferences” are said to be “detached” by “induction”—but that is in no way meant to even imply any application of actual logic. As Notturno remarked: “Popper used to call a guess ‘a guess’. But inductivists prefer to call a guess ‘the conclusion of an inductive argument’. This, no doubt, adds an air of authority to it.” The same is, unfortunately, true for ‘hypothesis’, “or just ‘claim’”, which Mayo “will use…for any conjecture we wish to entertain” (SIST, 9)—explicitly, as she said earlier, “whether or not they are part of any scientific theory”. If you think that usage of ‘hypothesis’ carries rather strongly “the connotation of the wantonly fanciful”, Mayo specifically rules that in; Medawar, whose phrase that is, rather optimistically thought it was the bad old days when there was no “thought that a hypothesis need do more than explain the phenomena it was expressly formulated to explain. The element of responsibility that goes with the formulation of a hypothesis today was altogether lacking.” (Schilpp: The Philosophy of Karl Popper, 279) With respect to science’s being grounded in theories, Mayo is working mightily to resurrect an irresponsibility that was presumed happily dead long ago. Medawar quotes Claude Bernard with a prescient passage that seems all too fitting a description for what’s wrong with today’s social sciences: “A hypothesis is…the obligatory starting point of all experimental reasoning. Without it no investigation would be possible, and one would learn nothing: one could only pile up barren observations.” (Schilpp, 288)
To Mayo, though, that isn’t worth a single word. At least she is in good (or rather: numerous) company. Anything and everything to do with ‘theory’ is a huge blind spot in current social science. Everybody seems to be focused on bad, misunderstood, and allegedly broken statistics—and boy, is there a lot of bad and misunderstood statistics around. There are precious few voices in the wilderness, among them Denny Borsboom, who bluntly states: “It is a sad but, in my view, inescapable conclusion: we don’t have much in the way of scientific theory in psychology.” This “Theoretical Amnesia”, as he calls it, is the elephant in the room of the replication crisis. It even explains why some of the methodological suggestions to stem the tide of bad science, like preregistration, spectacularly miss the point:
Mind you, Borsboom himself thinks that some disciplines just “are low on theory”. Why that should be an inescapable fact, however, he does not say. And it goes without saying that any discipline we might care to think of today was in its history at a point where it was “low on theory”. Biology and chemistry had no theory to speak of as recently as roughly 150 ago. But it takes not just lots and lots of work (which people are obviously willing to put in) but also the good fortune to be working on problems that are rife for yielding answers—and an idea of what a unifying, explanatory theory actually looks like, which is no different in the social sciences than in any others. As it is, even Mayo’s book-length attempt to “get beyond the statistics wars” is hardly more than a baby step. Even the “severe tester” of Mayo’s imagination remains condemned, in Bernard’s sadly apt phrase, “to wander aimlessly”.
You raise two issues that are to an extent separate — Mayo’s concept of ‘induction’, and the more general issue of whether some form of induction has a necessary place in scientific processes. I would argue that it does, albeit with a large deductive component. It is Mayo’s concept of ‘induction’ that is, however, more pertinent to the discussion of her book.
As I understand her, Mayo wishes to severely limit use, both of the deductive processes of mathematical modeling and of data sources. I find her arguments for this unconvincing. These are maybe not part of her philosophy. Why not? The effect is to severely compromise the use and the bringing together of different sources of evidence.
For Mayo, the modeling that leads to p-values is, if the proper conditions are satisfied — it is a central pillar of her ‘philosophy’. The p-value that results can be used only to give a credibility (or not) to the alternative that is not to be expressed as a probability. She frowns, though allowing that there are special contexts where this is a fruitful way forward, on any attempt to move from a p-value to estimate the probability that the null is false — even where a data-based estimate of the relevant prior is available. Mayo accepts that arguments of this type have a role if one’s luggage triggers an alarm when screened at an airport — most alarms are false alarms. She acknowledges the usefulness, also, of a related methodology in gene expression studies where the aim may be to identify which of perhaps 10.000 or 20,000 genes have been expressed. Why, then, an apparent objection in principle to the use of evidence that suggests that published studies of a specified type were overwhelmingly, as in [Begley and Ellis (2012)](https://www.nature.com/articles/483531a) not reproducible. Out of 53 ‘landmark’ cancer studies, only six could be reproduced, even after checking back with the authors involved to ensure that the methodology had been correctly reproduced. There are several ways that such evidence might be used.
Evidence such as reported in the Begley and Ellis paper is on its own enough to warn anyone who hopes to reproduce one of those landmark papers that, unless they can find other evidence that distinguishes the paper of interest from the rest, they should expect to be disappointed. Indeed, [Begley (2012)](https://www.nature.com/articles/497433a?draft=journal) identifies red flags that, where the methodology is reported in sufficient detail that any red flags would be obvious, would identify at least some of the 47 papers for which results could not be reproduced. Clearly, the p-values in those papers cannot be trusted, and the more relevant evidence is that provided in the Begley and Ellis (2012) paper.
Consider, alternatively, a hypothetical 53 papers that raise no red flags, where the issue is simply that a high proportion of null hypotheses are for all practical purposes true. A high proportion of the cases where an effect is found are, then, from the 5% of those results where the test statistic falls in the relevant 5% tail. It is then entirely legitimate to use the 6 out of 53 success rate to assign a prior probability, and accordingly to use Bayes’ theorem to move from a prior probability to a false discovery rate. Such a calculation may most simply be based on a pre-assigned choice of significance level α, as in [Ioannidis (2005)](https://journals.plos.org/plosmedicine/article?id=10.1371/journal.pmed.0020124). [Colquhoun (2012)](https://royalsocietypublishing.org/doi/abs/10.1098/rsos.171085) gives a more finessed calculation that uses the calculated p-value as the starting point. If no good evidence is available on which to base a prior, it is insightful to plot the false discovery rate against the prior. If p-values are to be used at all, it is surely desirable to get some rough sense of how they may relate to probabilities that are of more direct interest.
Mayo argues (p.369) that ‘[taking] the diagnostic screening model literally,’ thus moving from a small p-value to a much larger false discovery rate, is likely to compromise important work that, notwithstanding a string of failures, will finally yield its secret to a skilled and dogged experimentalist. I think this bizarre — the fact that evidence may be misused is not a reason for ignoring it!
On p.366, Mayo gives a numerical example, on the basis of which she claims that “the identification of ‘effect’ and ‘no effect’ with the hypotheses used to compute the Type I error probability and power are inconsistent with one another.” But this seems to rely on a mistake in her calculations. For the alternative against which the test has a 0.9 power has, assuming normality, α ≈ 0.115, rather than “almost 0.9”.
» John Maindonald:
…whether some form of induction has a necessary place in scientific processes. I would argue that it does, albeit with a large deductive component.
I do believe you when you say that you would argue that, but it would be much more interesting if you actually did. :)
And what does “induction…with a large deductive component” even mean?
Always, there is a leap from the mathematical modeling and associated data that underpin statistical inferences to the inferences made. Integral to that leap are multiple assumptions:
1) ‘Diagnostic checks’ on the modeling, while a crucial part of the exercise, are inevitably limited in what they can reveal.
2) Strong assumptions are made on what the population from which the data are drawn can, given the sampling process, reveal about the target population. What can a sample from a past population tell about the current population. (If enough time has elapsed, I’d suggest ‘Little that is useful.’ If we are lucky, the passage of a few weeks, or a few years, will not matter.)
3) We commonly take it for granted that data collection and associated modeling strategies that seem to have worked well in the past will be effective in the future, perhaps in somewhat different contexts.
Yes — so we always need to be aware of what assumptions we are making, and also need to be up-front about them, and discuss their limitations and what effect they might have on our conclusions.
(Regrettably, these are all too often not done — often with the rationalization, “That’s the way we’ve always done it” (TTWWADI) in our field.)
As is always the case when it comes to this issue, each one of your answers glaringly obviously begs the question. Of course, this has been pointed out by any and all critics of alleged induction; inductivists usually carry on as if ignoring the obvious lack of validity of a presumed procedure were completely immaterial. Mayo does too, by the way: confronted with the fact that inductive arguments are not valid, she nonchalantly moves the goalposts and retorts that deductive arguments on the other hand can’t guarantee the truth of their conclusions. Which not just frivolously dodges the problem but also betrays a complete lack of awareness of the untenability of the concept of ‘certain knowledge’.
What that I have said “betrays a complete lack of awareness of the untenability of the concept of ‘certain knowledge.” Surely, it is deductive argument that provides certain knowledge, but this is not, and cannot be, knowledge about the world. How do you make the step from deductive argument to knowledge of the world? The philosophical problem surely goes deeper that arguing that deduction alone can provide a (presumably tentative) answer. What is your name for what it is that adds the missing step? I note that Notturno, whom you quote, accepts that “inductive arguments may persuade or induce us to believe things.” The issue may be whether induction is an appropriate term for the leaps of judgement that I have in mind.
Not what you said but what Mayo said betrays such a lack of awareness.
Nothing provides certain knowledge. There is no such thing. Not even about things that are not about the world. Not even anything in logic and mathematics can claim to be absolute, certain knowledge, as every knowledge claim rests on assumptions. And those, like anything else, are fallible.
What deductive arguments can do is provide us with a logically valid way to learn. That’s Notturno’s point I quoted above. And he doesn’t “accept” anything about induction, he just says that the only thing it can do is make us believe things—which is purely psychological, subjective, and has nothing to do with either logic or knowledge.
If you’d be interested in delving deeper into these questions, I’d seriously recommend you read Popper’s Objective Knowledge; it’s a very good book and will answer most questions you will have on this topic, I suspect. :)
You imply that Popper’s is the only valid account of the way that science can/does proceed. How many of those who publish on the philosophy of science would accept that position? Do you accept that while absolute certainty is not attainable, there are degrees of certainty? Are probabilities a valid way, in principle, to express degrees of certainty? Mayo appears to say “No,” except perhaps in special cases such as she notes in her “Fine for Luggage” comment on p.361.
I do not imply that; I do say, however, that Popper’s account (slightly amended and improved) is the only coherent and consistent account so far of how science can make progress.
The following question is irrelevant. The number of people who agree/disagree with a position is of no import; what matters is whether a) they understand the relevant problems and b) they have pertinent arguments to support their position. About that we can have a conversation.
“Degrees of certainty” are supported by the same argumentative structure as simple “certainty” and consequently fail for exactly the same reasons.
No, probabilities are not a valid way to express degrees of certainty either—unless you’re prepared to make “probability” into something entirely subjective, which would of course be completely incompatible with every other technical use of “probability”.
I consider a probability as a way of expressing a degree of *uncertainty*; “degree of uncertainty” makes sense to me, although “degree of certainty” does not. (So I do not consider P(A) to be “degree of certainty of A”, but I consider it to be “degree of uncertainty of “not A”)
However, to use the models of probability to do calculations, one needs to be sure that the probabilities of various events are “coherent”. “Subjective probabilities” can make sense, as long as they are “coherent” as a system.
(See https://web.ma.utexas.edu/users/mks/statmistakes/probability.html for an attempt at a not-too-technical elaboration.)
Mayo devotes a number of pages, in at least four different places in her book, to the claim that P-values exaggerate the evidence that the null is false. In words (p.168) that she quotes from Harold Jeffreys, and claims to debunk
> What the use of P implies, therefore, is that a hypothesis that may be true may be rejected because it has not predicted observable results that have not occurred.
[Jeffreys, H. (1961). Theory of probability (3rd ed.), p.385]
Jeffreys goes on to argue that the non-observance of more deviant results (more deviant than the test statistic d0, where Pr[d; d >= d0] = p)
> might more reasonably be taken as evidence for the law, not against it.
(The ‘law’ is the null hypothesis H0.) This with reference to a standard one-sided test statistic.
Mayo claims to debunk this argument, in the initial discussion on pp.168-170 judging p-values relative to what they claim to measure. Using an imprecise form of argument, Mayo claims that
> Considering the tail area makes it harder, not easier, to find an outcome statistically significant. . . . Why? Because it requires, not merely that Pr[d = d0; H0] be small, but that Pr[d >= d0; H0] be small.
Mayo has the argument the wrong way round. For a test statistic that has a continuous distribution, Pr[d = d0; H0] = 0. No doubt, it is the density that is in mind! This is, however, not directly comparable with a tail probability. A more nuanced examination is required.
Now, take d_α to be the test statistic such that Pr[d; d >= d_α] = α. Thus, for α = 0.05, assuming a normal distribution, d_α = 1.64. Under standard modeling assumptions, Pr[d >= d_α; H0] is indeed the probability that a calculated p-values will be less than a pre-assigned cutoff α. This comes at the cost of ignoring the more nuanced information provided by the calculated p-value.
Now, the key point! One can evaluate E[d; d >= d_α]. For α=0.05, this equals (to 2d.p.) 2.08, corresponding to p=0.019. Thus p-values that are close to 0.05 will occur relatively more frequently than the 0.05 average over the tail, while p-values that are smaller than 0.019 will occur less frequently. The numbers will change if one has, e.g., a t-distribution rather than normal distribution. The general point made remains valid. While the difference between 0.05 and 0.019 may or may not be of great consequence, it surely is important to understand the different interpretation that should apply when moving from a pre-assigned cutoff α to the calculated p-value.
On pp.246-248, Mayo refers again to arguments that P-values exaggerate. The focus moves to arguments that are based on Bayesian posteriors, Bayes factors, or likelihood ratios. For the Bayesian statistics, common choices of priors are a focus of her criticism. Her more general argument is that one philosophy should not be criticized from the perspective of another. This is surely to challenge the legitimacy, in principle, of criticisms that she directs at those who do not accept her philosophy!
The claim to have debunked Jeffreys is repeated on pp.332-333. On pp.440-441, Mayo revisits the arguments of pp.246-248.
My third to last paragraph (starting “Now, the key point!”) uses an inappropriate expectation, and complicates the argument unnecessarily. The expectation is best calculated on the scale of the p-value itself, where the relevant distribution is uniform on the interval [0,1].
E[p; p <= α] = 0.5α, irrespective of the degrees of freedom for the t-statistic. A strategy that says: "Reject H0 when p = d_α] gives the expectation of a distribution that has a very asymmetric distribution. The difference from E[p; p <= α] illustrates the point f(E[x]) does not then equal E[f(x)].
I work as a statistics support officer (providing statistics support to all higher research students and our research staff) in an Australian university. So far I have dealt with more than 200 consulting projects (large or small).
As a applied statistician, when I read Mayo’s articles or book, I have the same feeling as Shravan Vasishth put it in his comments above (quote):
“… it’s not that I haven’t read anything by Prof. Mayo. I tried to read her work when Andrew started mentioning it, but I couldn’t understand anything. I always felt like I had walked into the middle of a conversation and was missing some crucial assumed background knowledge.” and
“I would like to see these statisticians show us what severity testing adds beyond what we can already do, in specific cases.”
I also noted that in Mayo’s “P‐value thresholds: Forfeit at your peril” (https://onlinelibrary.wiley.com/doi/10.1111/eci.13170) she fiercely attacked ASA 2019 Editorial’s call for “stop using the term ‘statistically significant’ entirely” (https://www.tandfonline.com/doi/full/10.1080/00031305.2019.1583913). In my understanding, ASA 2019 Editorial’s core message is simple and clear: Null Hypothesis Significance Test (NHST) is logically invalid because any continuous measure of discrepancy between the observed data and a fitted model cannot be categorized for the purpose of testing a statistical hypothesis (or to making a statement about the “truth”). I have no reservation in supporting ASA’s call. Therefore, my question for Mayo is very simple, does her severity testing framework categorize a continuous measure for testing? If the answer is “yes” (which I assume so), that would be exactly what ASA’s 2019 Editorial is against. I believe that is the exact reason why Mayo attacked ASA’s 2019 Editorial so desperately.
In my view, ASA has done a fundamentally important job by calling to abandon the concept of ‘statistical significance’ entirely. Because I am convinced that NHST is logically not defensible, technically flawed, and practically damaging. Even more fundamentally, statistical inference’s role has been exaggerated and distorted too much for too many years just as many literature has already argued e.g.,: https://www.tandfonline.com/doi/full/10.1080/00031305.2018.1464947 and https://journals.sagepub.com/doi/full/10.1177/0149206314547522.
As human beings using human language we make categorised statements all the time. Of course you can indicate a continuous posterior probability of 93.7% or p=0.039, but a practitioner will then in almost all cases ask you “so should I believe this now or not?” Even if you make carefully graded statements such as “there’s overwhelming/strong/some/almost no/no evidence against… in the data” you have in fact categorised. This being so, you may well ask the question, assuming that the H0 is true, or wrong in a specific way, how often does it in fact happen that I observe p<0.05 and say "there's some evidence"?
The thing is, in order to investigate performance characteristics of a method in terms of error probabilities, you need a threshold. There's no magical interpretative meaning to that. We all know that p=0.04 is closer to 0.06 than to 0.02 regardless of arbitrary thresholds, however a threshold is needed in order to evaluate the procedure (or let's say, if you want to do it in the rather straightforward error probability way – I don't deny something can be done with continuous values, but it will be much more convoluted). And in fact, in practice we are asked for categorised statements and also people who don't use NHST will use them to satisfy their collaborators.
"Even more fundamentally, statistical inference’s role has been exaggerated and distorted too much for too many years just as many literature has already argued" – that's a fair enough point and I'd probably agree with it, however it doesn't bear much on discussions of "given that we do statistical inference, how should we do it?"
Increasingly, as the book progresses, she gets into territory where the detailed arguments are, to my mind, obscure. As I commented in my review of the book, the book needs to be accompanied by detailed R or other code that makes it clear where the numbers come from. I found one mistake (I drew attention to it somewhere above) that threw me, while fixing it destroyed her argument. I suspect, as is perhaps inevitable in a book that relies so heavily on the intricacies of numerical case studies, that there are others. I wonder how many readers have followed the details of her arguments from cover to cover, rather than commenting on the broad sweep.
The “severity testing” perspective, which I strongly endorse, is perhaps the only point of common ground with the broad sweep of the ASA 2019 Editorial’s core message. In spite of differences in the methodologies that the authors of the articles that follow prefer, there is broad agreement with that core message. As you say, she is strongly and strikingly at odds with that message.
Comments that enlarge on my review, and a link to the review, may be found at
https://link.growkudos.com/1gppk1ij0n4
Mayo places on the data and models that may be used to inform statistical analysis that are retrogressive. She wishes to severely limit the use that may be made of prior information. One effect is to limit the scope of severe testing.