A basketball fan of my close acquaintance woke up Wednesday morning and, upon learning the outcome of the first games of the NBA season, announced that “The Warriors suck.”
Can we answer this question? To put it more precisely, how much information is supplied by that first-game-of-season blowout? Speaking Bayesianly, who much should we adjust our expectation that the Splashies will dominate this year?
This is an interesting question in its own right but also is an example of something I’ve been thinking about regarding base-rate fallacy and the rate of integration of information over time, and it relates to some of our favorite topics such as odds for presidential vote, Brexit, Leicester City, etc. My feeling is that the judgment-and-decision-making literature has a lot about base rate and weighting of prior and data, but not much on the time evolution of assessments: the process by which we move from base rate to data-based estimates. As has been discussed a few times on our blog, the failure of pundits or betting markets for Brexit, Leicester, and Trump-in-primaries were a too-slow incorporation of data as they were coming in.
So how to think about Warriors? I can think of two ways to go about this:
1. Fully model-based:
a. Fit a model to estimate team abilities from a season’s worth of data, basically the same model as the World Cup model that I fit in Stan a couple years ago, using as a team-level predictor some prior ranking of teams (from Sports Illustrated or whatever). Fit this model to last season’s data. Or, better still, fit it separately to each of the past several seasons (the “secret weapon“), for each season using that season’s prior rankings as a team-level predictor. Our model will be very similar to the World Cup model (again, we’ll predict score differential, not wins) but we’d also want to include home-court advantage.
b. From this fitted model, estimate the hyperparameters (or, we have estimates of the hyperparameters from each past season, and I guess take some sort of average). From these, we get a prior estimate and uncertainty of team ability, given its preseason ranking.
c. Then fit the model to the NBA data after the first round of games this year (which includes the Warriors-Spurs debacle from the other day). Now look at the new estimate for the Warriors and see how much has it changed?
2. Hacking something together:
The idea will be to estimate the information from this one game, to express this in the form of a likelihood function. It goes like this. The 30 teams in the NBA have some range of team qualities (“abilities,” in psychometric terminology). The prior rankings had the Warriors at #1 (according to Sports Illustrated) or #2 (ESPN) with the Spurs are ranked at #3. So, the question is, do the Warriors really “suck”? What’s the likelihood of the data?
Home teams win about 60% of basketball games, and in googling I see one source saying this is a 2.3-point advantage and another calling it 3.6 points. Let’s split the diff and call it 3 points. So if the Warriors and Spurs are approximately equal (that’s what you’d say for teams ranked 1 and 3, or 2 and 3, playing each other), you’d expect the Warriors to win by about 3 points when playing at home, hence a 29-point loss is 32 points worse than expected.
How bad is 32 points worse than expected? According to Hal Stern, the sd of NBA score differentials relative to point spread was 11.6; let’s call it 12 points. So 32 points is -2.67 sd’s compared to the expectation.
Now what about if the Warriors “sucked,” i.e. were an average team? How much would we expect them to lose to an elite team such as the Spurs? Hmm…. I looked up last season. The Warriors were the leaders at +10.8 and the Spurs were second at +10.5. Anyway, that suggests that an average team would get beaten by 10 points by a top team. Or get beaten by 7 at home. So, losing by 29 is a -22, which is -22/12 = -1.83 sd’s compared to the expectation.
Then, the likelihood ratio for this game is, in R, dnorm(1.83)/dnorm(2.67) = 6.6. If, for example, our prior belief was 95% that the Warriors are a top team and a 5% chance that they are mediocre (or, as Jakey would put it, that they “suck”), then our prior odds ratio was 19 and our posterior odds is 19/6.6 = 2.9, so now we think the chance they are mediocre is 1/(1+2.9) = .26 or 26%, and there’s a 74% chance they are elite and just got bad luck.
But maybe that’s too extreme. Let’s try a different one. Suppose the options are elite, strong, or mediocre, where “elite” = top team, “mediocre” = avg team, and “strong” is in the middle, i.e. should have no problem making the playoffs but will not be expected to make the Finals. Now, I don’t know what the best prior probabilities should be here. The way to check this would be to look at past teams ranked 1 or 2 in preseason in previous seasons, and see how well they did. So let me just guess on this one, let’s say, based on their preseason ranking there’s an 75% chance they’re a top team, a 20% chance they are strong, and a 5% chance they’re mediocre, in terms of how they’ll actually perform in the 2016-2017 season. Now the likelihoods: If Warriors are a top team, they performed 32 points worse than expected; if they’re mediocre they performed 22 worse than expected (see calculation above, based on the idea that a top team should beat a mediocre team by 10 points on avg), and if they’re strong, let’s say they did 27 worse than average. Then the likelihoods for top, strong, mediocre are given by dnorm(c(32,27,22)/12) = (0.0114, 0.0317, 0.0743), and when we multiply these by our assumed prior probabilities (0.75, 0.20, 0.05) and renormalize, we get (0.46, 0.34, 0.20), implying there’s roughly a 50% chance the Warriors are a top team, roughly a 1/3 chance they’re merely strong, and a 1/6 chance they’re mediocre.
The next step would be to make this into a continuous model where the underlying parameter is the team’s expected point differential during the season (could be anywhere from -10 which is last season’s Sixers to +10 which is last season’s Spurs or Warriors). Again, key step is assigning a prior based on their preseason ranking, and to do this right we’d want to look at the performance of top preseason-ranked teams in previous years.
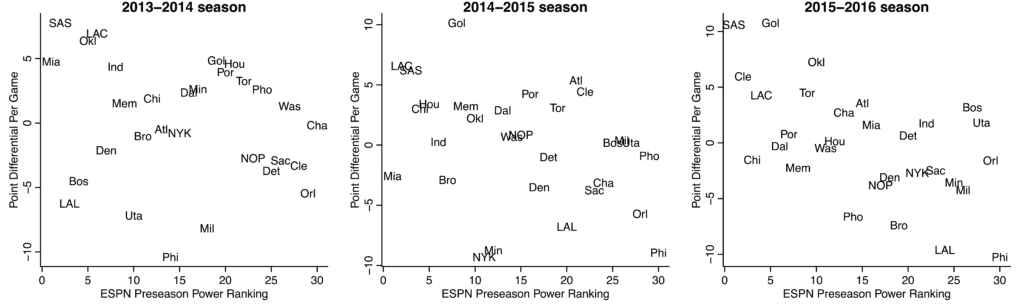
Daniel Lee looked up the ESPN preseason power rankings for the past few seasons, and then we plotted what actually happened (for each team, its regular season per-game point differential, which I think should be a less noisy measure than simple won-loss record):
Just to clarify, by “preseason power ranking,” I mean rankings constructed before the season begins; I don’t mean that these are rankings based on preseason play (although I suppose that preseason play might contribute in some way to the rankings).
Assuming these numbers have been transcribed correctly, it suggests that preseason rankings can be way off: there’s a lot of variability here. On the other hand, maybe the Warriors’ #1 or #2 rating this year is stronger than, say, the Heat’s #1 rating before the 2014-2015 season.
One could argue the first game of the season is not so informative because the teams are still getting their acts together. One way to handle this would be to increase the sd of that predictive distribution. Suppose, for example, we ramp it up from 12 points to 15 points. Then the likelihoods for “top,” “strong,” and “mediocre” become dnorm(c(32,27,22)/15) = (0.0410, 0.0790, 0.1361), and when we multiply by our assumed prior probabilities and renormalize, we get (0.58, 0.30, 0.13), thus roughly a 60% chance the Warriors are a top team etc.
Also I looked up the point spread for that Spurs/Warriors game on Tues. It looks like the spread was 8.5, which seems just wrong if the two teams are close to evenly matched and home-court is only worth 3 points. So either I’m missing something important, or it’s just that bettors were seduced by the Kevin Durant mystique and overbet on the Warriors.
Finally, to loop back to the larger question: Look how hard it is to update beliefs based on information. Even in this highly controlled, nearly laboratory setting, there’s no way I could do this in my head. So you can see how pundits and data journalists can trip up and be too fast or too slow to incorporate new information on elections.
P.S. Feel free to argue with any and all of my assumptions and reasoning. That’s the whole point of this sort of analysis: it’s transparent, all the assumptions and data are out there so you can go back and forth between assumptions and conclusions. I just had to get this post out before the Warriors played their second game.
If we presume that the Warriors and spurs were evenly matched last year(markets had gsw as faves last year, why would we presume them to not be a much bigger favourite after replacing a below average player (Barnes) with a top 5 nba player in Durant?
Jon:
All I can tell you is that SI and ESPN had Warriors ranked 1 and 2 this year, and they both had Spurs ranked 3. Rankings 1,2,3 are all pretty close, implying that neither team would be much favored in a head-to-head matchup.
Andrew,
The betting market had the Warriors 60%~ to win the title, and the field (every other team) as 40%. That implies nothing near equal teams.
Similarly, the season wins o/u pegged the Warriors at 68.5, by far the highest in the league (and all-time). The Cavs were second, IIRC, at 56.5. That’s a huge gap. I don’t recall where San Antonio was exactly, I think around 54. These numbers imply that GSW are 83.5% to win a random game vs a random opponent, and that SA is 66%. We can then use the log5 formula to estimate that GSW was a ~3:1 favourite in the first game based on the above numbers. Not surprisingly, 3:1 is about what a -8.5 pointspread implies.
Jon:
This could be. I was just using preseason ranking, but you’re making the good point that just using the ranking is throwing away some continuous information. It’s better to use more information, and I appreciate that you’re doing just what I asked for in my P.S. above!
Andrew, is there a typical relationship between rank and the continuous (presumably normal?) distribution that the ranks are derived from? It’s actually always been my assumption that if #1 in some sport plays #2 that #1 has an advantage but if #25 plays #26 it should be pretty even. Was your contrary intuition based on something statistical like the translation I described?
Alex:
I’d expect that if you take the ranks and give them an inverse-normal-cdf transformation, you’d get something like a linear predictor. There are 30 teams in the league, and I’d expect more spread in the upper and lower tails. For example, last year’s 76ers were on the lower tail.
Why not consider how often this kind of loss occurs for a top-rated team, both at the beginning of a year and anywhere in the season? You dig up some ratings system like an ELO or expected wins or whatever for pre-season favorites and see how often this happens. You can also then compare season outcomes. I question the utility in any way of a snapshot estimate of suckiness, something you get at when you expand the sd.
Jonathan:
Elo is just a name for an logistic regression item-response model. In this case you’d want to model point differential, not just win/loss, because point differential has a lot more information. But basically what you’re suggesting is my approach 1 outlined above. That just takes more work in putting together the dataset, but, yeah, it’s definitely the way to go. Again, the key is to use all the data. Don’t just tabulate what happens to preseason favorites, instead model all the teams and all the games, then do some model checking to make sure everything makes sense for the preseason favorites. I did approach 2 above just cos it didn’t require putting together a big dataset. The utility of that calculation is really just to show how difficult it would be to do in my head, which is relevant to the discussion in political journalism of how pundits like Nate Silver can keep getting things wrong. The answer is, it’s hard. It’s hard even in a setting as simple as pro basketball, and it’s even harder with elections, where the N is lower and the rules of the game keep changing.
Regarding this tidbit: “According to Hal Stern, the sd of NBA score differentials relative to point spread was 11.6”: is there evidence to indicate that this metric is normally distributed? My intuition is that it isn’t, although I don’t have any evidence handy to support that intuition.
I’m not sure about the NBA, but I’ve looked at NFL point differentials and they’re surprisingly normal for a game with such odd scoring rules.
There is lots of data available on margin of victory. Wikipedia lists scores for each game of the NBS playoffs. In the Western Conference Finals, which the Warriors won 4-3, their margin of victory over the Thunder (not the Spurs) in the games were:
-6
+27
-28
-24
+9
+7
+8
So the “better” team lost twice by more than 20 points.
Pchemist:
Yes, for sure a better way to attack this problem would be to use point-differential data from the past several seasons, rather than what I did was to make some quick calculations based on a decades-old sd number.
1) As you mention, the beginning of the season can be clunky. This is particularly true when adding a major new player like Durant. The Heat and Cavs were both about .500 teams for the first 30 or so games after Lebron joined and went to the finals.
2) The playoffs are all that really matter and smart great teams pace themselves and experiment during the regular season. That 2014-15 Heat team with the low regular season point differential went to the finals.
3) It’s silly to take exact final score differential as meaningful in a blowout. The lead was 22 points with 3 minutes left and the game essentially over. Then it balloons another 7 points (almost a full standard deviation’s worth of points in some of the calculations you were doing) in garbage time, and this is supposed to have an impact on what we take from the game? It could have gone back down to 10 in that time and we should have drawn the exact same conclusions as we would given what actually happened. What those conclusions are, I don’t know.
Z:
I know what you’re saying about garbage time; on the other hand, to be down by 22 points is already a problem! One could look at the statistics but my guess is that there is a positive correlation between team ability and how well they perform even in garbage time when far behind. So I don’t agree with you regarding “exact same conclusions.” But, sure, ultimately we’re getting to the granularity of the data.
I agree there’s *some* correlation between garbage time performance when down by a lot and team ability, but I think it’s really small. And of course I also agree that being down by 22 is already a problem. My point is just that your rough methodology is pretty sensitive to what happens after being down 22, which is barely related to the parameter of interest. Maybe a really careful analysis would only use data from portions of games where win probability is within some bounds.
I’m sure the data wouldn’t be as readily available as point spread, but an interesting measure to look at would be when the win probability hit some threshold. So, forget the final score, how many minutes were left in the game when the win probability first exceeded 95% or 98% or whatever. Using that as a measure might eliminate the garbage time problem and focus the analysis on how competitive a game was or wasn’t.
Andrew,
Very interesting analysis. Thank you for taking the time to write this out as it is very helpful to students like myself who want to practice their statistical thinking.
One question. What is the reason for the normality assumption, for example in your first method with z scores 1.83 and 2.67? So I know that you don’t actually think it’s normal, but I want to make sure I understand your logic for making this assumption. There are no averages in sight (it is a distribution over point differentials), so the central limit theorem does not apply here, correct?
What would you think about using a laplacian instead of the normal, perhaps because one might expect fatter tails than the normal allows for? In that case, we have
b=sqrt(0.5);dlaplace(1.83,scale=b)/dlaplace(2.67,scale=b)
[1] 3.280315
where I used http://artax.karlin.mff.cuni.cz/r-help/library/LaplacesDemon/html/dist.Laplace.html and b is set to sqrt(0.5) so as to achieve a variance of 1 and thus be consistent with the use of z scores.
So a likelihood ratio of 3.2 vs. 6.6. Quite a difference.
Do you think it makes sense to use the Laplacian, or am I missing something? Are there any other distributions that might be worth trying?
Thanks!
The normal is the maximum entropy distribution for a fixed mean and variance, correct? I guess that is one reason to use it, i.e. if all we know is the mean and variance as in this example, then we should choose the normal distribution because it’s the most uninformative? Hmm, this seems like a good principle in the abstract but not very useful here . . .
Student:
I strongly doubt that the Laplacian distribution fits the data. You say there are no averages in sight, but the score differential in the game really is the sum of a bunch of small pieces, so the normal distribution seems to me like a reasonable guess. Ultimately, though, it’s an empirical question which could easily be answered with a year’s worth of data.
Makes sense, thank you!
it looks like you already went through this with jon k., but rankings and ratings are two different things. if you try to predict game outcomes based on rankings you will get totally destroyed. its not too hard to get 100k down on an NBA spread so the vegas spread of 8.5 is pretty reliable, its a big efficient market.
normally in pro sports there is more parity. but for an analog look at college football. alabama is #1 seed, and a couple weeks ago they played, if i remember correctly, #14 seed arkansas, and they were still favored by 17 pts and they won by even more than that.