I promised I wouldn’t do any new blogging until January but I’m here at this conference and someone asked me a question about the above slide from my talk.
The point of the story in that slide is that flat priors consistently give bad inferences. Or, to put it another way, the routine use of flat priors results in poor frequency properties in realistic settings where studies are noisy and effect sizes are small. (More here.)
Saying it that way, it’s obvious: Bayesian methods are calibrated if you average over the prior. If the distribution of effect sizes that you average over, is not the same as the prior distribution that you’re using in the analysis, your Bayesian inferences in general will have problems.
But, simple as this statement is, the practical implications are huge, because it’s standard to use flat priors in Bayesian analysis (just see most of the examples in our books!) and it’s even more standard to take classical maximum likelihood or least squares inferences and interpret them Bayesianly, for example interpreting a 95% interval that excludes zero as strong evidence for the sign of the underlying parameter.
In our 2000 paper, “Type S error rates for classical and Bayesian single and multiple comparison procedures,” Francis Tuerlinckx and I framed this in terms of researchers making “claims with confidence.” In classical statistics, you make a claim with confidence on the sign of an effect if the 95% confidence interval excludes zero. In Bayesian statistics, one can make a comparable claim with confidence if the 95% posterior interval excludes zero. With a flat prior, these two are the same. But with a Bayesian prior, they are different. In particular, with normal data and a normal prior centered at 0, the Bayesian interval is always more likely to include zero, compared to the classical interval; hence we can say that Bayesian inference is more conservative, in being less likely to result in claims with confidence.
Here’s the relevant graph from that 2000 paper:
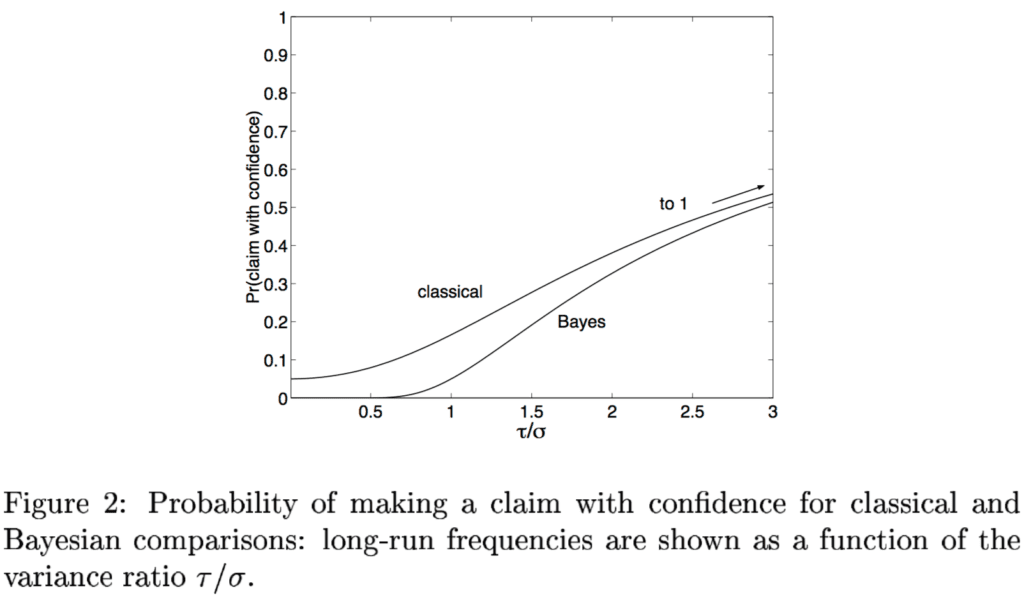
This plot shows the probability of making a claim with confidence, as a function of the variance ratio, based on the simple model:
True effect theta is simulated from normal(0, tau).
Data y are simulated from normal(theta, sigma).
Classical 95% interval is y +/- 2*sigma
Bayesian 95% interval is theta.hat.bayes +/- 2*theta.se.bayes,
where theta.hat.bayes = y * (1/sigma^2) / (1/sigma^2 + 1/tau^2)
and theta.se.bayes = sqrt(1 / (1/sigma^2 + 1/tau^2))
What’s really cool here is what happens when tau/sigma is near 0, which we might call the “Psychological Science” or “PPNAS” domain. In that limit, the classical interval has a 5% chance of excluding 0. Of course, that’s what the 95% interval is all about: if there’s no effect, you have a 5% chance of seeing something.
But . . . look at the Bayesian procedure. There, the probability of a claim with confidence is essentially 0 when tau/sigma is low. This is right: in this setting, the data only very rarely supply enough information to determine the sign of any effect. But this can be counterintuitive if you have classical statistical training: we’re so used to hearing about 5% error rate that it can be surprising to realize that, if you’re doing things right, your rate of making claims with confidence can be much lower.
We are assuming here that the prior distribution and the data model are correct—that is, we compute probabilities by averaging over the data-generating process in our model.
Multiple comparisons
OK, so what does this have to do with multiple comparisons? The usual worry is that if we are making a lot of claims with confidence, we can be way off if we don’t do some correction. And, indeed, with the classical approach, if tau/sigma is small, you’ll still be making claims with confidence 5% of the time, and a large proportion of these claims will be in the wrong direction (a “type S,” or sign, error) or much too large (a “type M,” or magnitude, error), compared to the underlying truth.
With Bayesian inference (and the correct prior), though, this problem disappears. Amazingly enough, you don’t have to correct Bayesian inferences for multiple comparisons.
I did a demonstration in R to show this, simulating a million comparisons and seeing what the Bayesian method does.
Here’s the R code:
setwd("~/AndrewFiles/research/multiplecomparisons")
library("arm")
spidey <- function(sigma, tau, N) {
cat("sigma = ", sigma, ", tau = ", tau, ", N = ", N, "\n", sep="")
theta <- rnorm(N, 0, tau)
y <- theta + rnorm(N, 0, sigma)
signif_classical <- abs(y) > 2*sigma
cat(sum(signif_classical), " (", fround(100*mean(signif_classical), 1), "%) of the 95% classical intervals exclude 0\n", sep="")
cat("Mean absolute value of these classical estimates is", fround(mean(abs(y)[signif_classical]), 2), "\n")
cat("Mean absolute value of the corresponding true parameters is", fround(mean(abs(theta)[signif_classical]), 2), "\n")
cat(fround(100*mean((sign(theta)!=sign(y))[signif_classical]), 1), "% of these are the wrong sign (Type S error)\n", sep="")
theta_hat_bayes <- y * (1/sigma^2) / (1/sigma^2 + 1/tau^2)
theta_se_bayes <- sqrt(1 / (1/sigma^2 + 1/tau^2))
signif_bayes <- abs(theta_hat_bayes) > 2*theta_se_bayes
cat(sum(signif_bayes), " (", fround(100*mean(signif_bayes), 1), "%) of the 95% posterior intervals exclude 0\n", sep="")
cat("Mean absolute value of these Bayes estimates is", fround(mean(abs(theta_hat_bayes)[signif_bayes]), 2), "\n")
cat("Mean absolute value of the corresponding true parameters is", fround(mean(abs(theta)[signif_bayes]), 2), "\n")
cat(fround(100*mean((sign(theta)!=sign(theta_hat_bayes))[signif_bayes]), 1), "% of these are the wrong sign (Type S error)\n", sep="")
}
sigma <- 1
tau <- .5
N <- 1e6
spidey(sigma, tau, N)
Here's the first half of the results:
sigma = 1, tau = 0.5, N = 1e+06 73774 (7.4%) of the 95% classical intervals exclude 0 Mean absolute value of these classical estimates is 2.45 Mean absolute value of the corresponding true parameters is 0.56 13.9% of these are the wrong sign (Type S error)
So, when tau is half of sigma, the classical procedure yields claims with confidence 7% of the time. The estimates are huge (after all, they have to be at least two standard errors from 0), much higher than the underlying parameters. And 14% of these claims with confidence are in the wrong direction.
The next half of the output shows the results from the Bayesian intervals:
62 (0.0%) of the 95% posterior intervals exclude 0 Mean absolute value of these Bayes estimates is 0.95 Mean absolute value of the corresponding true parameters is 0.97 3.2% of these are the wrong sign (Type S error)
When tau is half of sigma, Bayesian claims with confidence are extremely rare. When there is a Bayesian claim with confidence, it will be large---that makes sense; the posterior standard error is sqrt(1/(1/1 + 1/.5^2)) = 0.45, and so any posterior mean corresponding to a Bayesian claim with confidence here will have to be at least 0.9. The average for these million comparisons turns out to be 0.94.
So, hey, watch out for selection effects! But no, not at all. If we look at the underlying true effects corresponding to these claims with confidence, these have a mean of 0.97 (in this simulation; in other simulations of a million comparisons, we get means such as 0.89 or 1.06). And very few of these are in the wrong direction; indeed, with enough simulations you'll find a type S error rate of a bit less 2.5% which is what you'd expect, given that these 95% posterior intervals exclude 0, so something less than 2.5% of the interval will be of the wrong sign.
So, the Bayesian procedure only very rarely makes a claim with confidence. But, when it does, it's typically picking up something real, large, and in the right direction.
We then re-ran with tau = 1, a world in which the standard deviation of true effects is equal to the standard error of the estimates:
sigma <- 1 tau <- 1 N <- 1e6 spidey(sigma, tau, N)
And here's what we get:
sigma = 1, tau = 1, N = 1e+06 157950 (15.8%) of the 95% classical intervals exclude 0 Mean absolute value of these classical estimates is 2.64 Mean absolute value of the corresponding true parameters is 1.34 3.9% of these are the wrong sign (Type S error) 45634 (4.6%) of the 95% posterior intervals exclude 0 Mean absolute value of these Bayes estimates is 1.68 Mean absolute value of the corresponding true parameters is 1.69 1.0% of these are the wrong sign (Type S error)
The classical estimates remain too high, on average about twice as large as the true effect sizes; the Bayesian procedure is more conservative, making fewer claims with confidence and not overestimating effect sizes.
Bayes does better because it uses more information
We should not be surprised by these results. The Bayesian procedure uses more information and so it can better estimate effect sizes.
But this can seem like a problem: what if this prior information on theta isn't available? I have two answers. First, in many cases, some prior information is available. Second, if you have a lot of comparisons, you can fit a multilevel model and estimate tau. Thus, what can seem like the worst multiple comparisons problems are not so bad.
One should also be able to obtain comparable results non-Bayesianly by setting a threshold so as to control the type S error rate. The key is to go beyond the false-positive, false-negative framework, to set the goals of estimating the sign and magnitudes of the thetas rather than to frame things in terms of the unrealistic and uninteresting theta=0 hypothesis.
P.S. Now I know why I swore off blogging! The analysis, the simulation, and the writing of this post took an hour and a half of my work time.
P.P.S. Sorry for the ugly code. Let this be a motivation for all of you to learn how to code better.
Andrew, your effort for this impromptou post was worth it.
Out of all your historical posts on multilevel modeling and multiple comparisons, this particular post brings it all together very nicely.
Thanks
> “The analysis, the simulation, and the writing of this post took an hour and a half…”
Only!!! It would have taken me the full day!!
I was impressed by that too! It would have taken me all week.
+1.
When I started reading that PS. sentence I was expecting it to end with something like “a whole working day”
Nitpicking here. I wonder whether “What if this prior information on tau isn’t available?” is better said
with “What if this prior information on theta isn’t available?” ? Or maybe not. Thanks for the post.
On Thursday I will start teaching social science doctoral students “advanced quantitative methods” who have never taken calculus and linear algebra. Most have never written a lick of code in their lives. Yet all will claim some proficiency in stats because they’ve passed all their stats courses thus far. All have been taught incorrect interpretations of p-values and confidence intervals.
I’d love to challenge them to show that stats is much more than a tool, something like this that shows the serious ontological issues that need consideration. But since I have only fifteen weeks to do it and their comprehensive exams will graded by someone with the same flawed background rather than me, how on God’s green earth can I do it in a way that doesn’t harm them in the near future?
I love your blog and how you take on statistical nonsense but when I see more technical posts that deserve attention in my classroom, I’m frustrated that I’m stuck teaching “how to” rather than “why” because my students lack the fundamentals to actually get the material.
The problem goes so deep that I don’t think it can be solved. I just received an email from a company sells software that writes up the results from any analysis for a user, claiming it fosters interpretation. The write-up template looks like a statistical Mad-Libs that perpetuates the nonsense of statistical significance. It’s disheartening to know that that is how folks outside of our community view statistics, that all you need to do is to feed your data into software and it will spit out a write-up of results.
What can be done?
Yes, the gap between what is needed and what is possible for many students under the present constraints is frustrating. In case it might give you some ideas of what you might do under your constraints, feel free to look at the notes and links I have at http://www.ma.utexas.edu/users/mks/CommonMistakes2016/commonmistakeshome2016.html/; they are for a “continuing education” class (twelve hours) attended by a wide variety of people, including a variety of academics and a lot of people who work at state agencies. An introductory statistics course is the only prerequisite.
I was able to get your link to work by removing the last slash character:
http://www.ma.utexas.edu/users/mks/CommonMistakes2016/commonmistakeshome2016.html
Thanks for noticing and fixing the typo.
Isn’t it bizarre to teach “advanced quantitative methods” to students who have never taken calculus?
Why cannot the department change the needed pre-requisites?
It is probably “advanced” relative to what they know already (in social science). I know plenty of PhDs in linguistics who do experimental work and statistical analyses, and publish in major linguistics journals, but do not know how to do a paired t-test correctly. Once someone I was working with started arguing with me about why they couldn’t just run an experiment with 180 conditions and do all pairwise comparisons needed to find out what the facts were. This population also tends to regard statistics with a certain measure of contempt and disdain (it’s just numbers). Here we are struggling with the unknown unknowns, in Rumsfield’s categorization.
It isn’t usually possible to teach calculus and friends to students who have already elected out of being numerate (that’s why they are in that program).
Yes, but why do the Departments allow them to elect out?! Would we allow a structural engineer to elect out of mechanics? Or a Physician to skip biology pre-requisites?
It’s almost we are getting all this crappy Soc. Sci. research by design! If you don’t give them the right tools for the job obviously things end up being a disaster.
What’s the downside of just making things like Calculus a pre-requisite? I just don’t get it.
Because the professors themselves don’t know any of this stuff (with exceptions of course). Who would teach it?
By elect out I mean that people go to these areas with the explicit goal of avoiding any technically demanding stuff. When we teach programming to undergrads in linguistics, some express shock because this is not what they signed up for (this subset thought they were going to do an analyse de texte or something philological).
In political science, they seem to have an amazing array of sophisticated people (the Stanford prof for example who wrote that Bayes book that is a bit too advanced for me). You won’t find many people like that in areas like psych and ling and “social sciences” (whatever that is).
PS Having said all this, we do teach the math in our grad program in Potsdam, as part of a new MSc in Cognitive Systems. Most linguistics students drop out almost instantly. It’s a lot of work to learn this stuff (just high school, i.e., A-level, calculus and prob. theory actually), but one can get an MSc in Linguistics without knowing any of it, so why do it? If we made it obligatory, nobody would do the MSc I suspect.
In the U.S., you can send them to other departments. In the computational linguistics program MS/Ph.D. program at Carnegie Mellon, we made our students take intro CS for majors (201 and 202) if they didn’t have a coding background, which introduces algorithms, data structures, functional programming, etc. It nearly killed them, but they came out knowing much more than we could’ve taught them at no effort on our part. We also made them take senior-level math stats in either the math department or philosophy department rather than trying to squeeze it in edgewise into my semantics class (though I did wind up teaching all the higher-order logic).
So I’m partly with Rahul on this one. You don’t see people trying to teach graduate level physics to students who don’t know calculus—it’s just assumed you know that (and probably some serious analysis if not differential geometry). But I”m also sympathetic to the demands of an interdisciplinary program—you can’t teach someone who wants to do psycholinguistics the same amount of linguistics you teach a linguistics Ph.D. student or the same amount of psych you teach a psychology grad student or the same amount of stats you teach a stats Ph.D. student or the same amount of comp sci you teach a computer science Ph.D. student. It’s not clear where the balance is, but what I always told our students, you better wind up being able to pass as at least one of those kinds of more focused Ph.D. students if you want to apply for most jobs in academia.
In the U.S., political science is considered a social science, as is psychology. Linguistics gets classified into the arts along with lit crit and history.
The Professors don’t need to know! Isn’t that the whole point behind pre-requisites? Just make them take the appropriate Calculus class in the Math Dept.
OK, sure. One could send them to the math dept. The professors still don’t really know what you are talking about when you talk stats with them, but they are still using statistical tools. The profs can’t evaluate the student’s claims now; should the profs be trusting that the students know best, once they’ve come back from the math dept? Usuallly, when one has a prerequisite for a course of study, the assumption is that the professor also has that prerequisite knowledge.
@Shravan
Sorry, maybe I wasn’t clear about my point: I didn’t mean that the Math class would make them literate about p-values, or t-tests or the intricacies of the pitfalls etc.
My simple point is that for @digithead it will be really hard to get these concepts across to a student body that is, as you put it, “elected out of being numerate”.
Ergo, if you make them take Calculus or similar foundational courses then an “Advanced Quant Methods” course will start making a lot more sense. It makes “digithead”‘s life easier and the students learn more too.
Of course, there may be some students who are just not capable or motivated to deal with Calculus-101 but then I wonder whether we should really be asking them to work on Soc Sci problems that actually need “Advanced Quant Methods”.
Rahul: See the last sentence of Bob’s comment here.
(For his earlier sentences, I have yet to think of a concise or productive response.)
Forgot to put in the comment link http://statmodeling.stat.columbia.edu/2016/08/19/things-that-sound-good-but-arent-quite-right/#comment-297636
Non-Chomsykan syntacticians have been badly burnt by the Chomsykan dominance of the field, but as a psycholinguist, I am pretty far from all the acrimony. I can’t remember the last time I read anything by a Chomskyan, or even had to talk to one except maybe in a hail-fellow-well-met sort of way. Bob must have taken a lot of heat in his time as a linguist, though, and he’s right that people are theoretically very entrenched in linguistics. If you have a position on a question, you are expected to be 100% sure of it, there is no room for a probability distribution of beliefs over alternatives. It’s one reason that arguments between linguists are so vicious.
It really depended where you were at and who you were talking to. Yes, I’d get papers and grant proposals back with reviews that said only “this isn’t linguistics” (one NSF review actually said my work was “too European”—I went to Edinburgh for grad school). Half the linguists at Ohio State boycotted my job talk there, saying I wasn’t a linguist (Steve Bird and Richard Sproat, also on the shortlist, got the same treatment—others who brought us in wanted to hire a computational linguist who’d worked on morpho-phonology). NSF wouldn’t even review one of Carl Pollard’s and my grant proposals, insisting HPSG wasn’t linguistics. The joint program between CMU and Pitt broke up when they wouldn’t let one of Carl’s and my students do a qual paper on HPSG (this time they told us what kind of non-linguistics it was — engineering). But after all that MIT Press published my semantics book. And I got tenure (though in a philosophy department, not a linguistics department—I wouldn’t have stood a chance in linguistics).
All of the academic fields I’ve been exposed to (linguistics, cognitive psych, computer science, and statistics) have a certainty bias along with a sweep-the-dirt-under-the-rug bias so that people don’t hedge claims or list shortcominings for fear of papers being rejected.
“Half the linguists at Ohio State boycotted my job talk there”
I got my PhD from OSU, and we actually overlapped in 1997 when you visited for your talk. We had dinner together (with Carl Pollard). I must say I am surprised that even OSU had that reaction to you and Bird and Sproat. But it looks like the so-called non-linguists won in the end there, because the current profs in computational linguistics at OSU would by the 1997 standards also not be considered linguists.
About the NSF rejections, it seems that reviewers routinely use the review process to control the direction that the field is going in (the same happens in Europe). The program officer/funding agency often also has entrenched interests and/or has political concerns in mind when they make their decisions. Science is more about politics and control, the science happens in spite of this whole expensive machinery for funding and jobs.
It is probably for the best that you ended up where you are and not linguistics.
It’s not like giving them the right math background automatically immunizes them from making mistakes. After all, it is professional statisticians are the ones that are responsible for creating the mess with NHST that we are currently in. It’s not like some ignorant psychologists or the like took control and messed things up—the statistics delivered the wrong message. One could even argue that psychologists etc. just did what the professionals told them to do.
+1
Also, I have found when you replace the math with simple arithmetic, there remain large conceptual gaps.
Additionally, what percentage of mathematically well trained statisticians, can make sense of and properly interpret empirical research?
For instance, many just want to pull the Bayesian crank and point to the resulting posterior probabilities as being all of the answers (with probability one or almost surely or whatever exaggerated sense of certainty of this.)
No wonder some are amazed you don’t have to correct Bayesian inferences for multiple comparisons _but_ if only if your prior and data generating model are appropriate for the setting you are working in.
The frequentest approach of ensuring the confidence coverage is the same for all possible parameter values creates a procedure that is only appropriate for settings in which incredibly large effects are expected to be just as likely as small ones.
“Turn a deaf ear to people who say, “scientific men ought to investigate this [effects of any size], because it is so strange [to have effects that large].” That is the very reason why the study should wait. It will not be ripe until it ceases to be so strange.” CS Peirce
“Also, I have found when you replace the math with simple arithmetic, there remain large conceptual gaps.”
One of my favorite exercises is to ask people to express x in terms of y in: y=x/(1-x). Some 15 out of 30 undergrad computer science students in a NY university failed to solve this correctly. It is pretty surprising to watch graduate students flounder with this little problem-let.
“Additionally, what percentage of mathematically well trained statisticians, can make sense of and properly interpret empirical research?”
Very important point. Without domain knowledge one will get nowhere, no matter how much math etc one knows.
I also present posterior credible intervals, but I treat the problem as an estimation problem rather than a hypothesis testing problem. When writing a paper, one is forced to decide whether to act as if a particular effect is present, effectively arguing for or against a hypothesis, but I try to remember that the next time I run the same study (which is, like, never), I will probably get a very different result. It’s hard to have many strong beliefs in such a situation.
> express x in terms of y in: y=x/(1-x)
On the other hand, I encouraged my daughter to do an undergraduate math course and unfortunately she took one of those for science students calculus courses. Almost all of what they took involved re-expressing tricky expressions.
I was disappointed as it was unlikely to be of later value in anything she did, she was bored out her mind trying to get an A+ (which she did) and she swore she would never take a math course, ever again.
We have computer algebra for dealing with the tricky details – why waste the energy there rather than on the function and logic of math?
Keith, the problem with math is that most people learn it from mathematicians! :-)
From the forward to “Street Fighting Mathematics”
@Keith
I know what you mean. I think the problem here is that most math curricula were designed in a pre-computer algebra age and are relics of a time not so long ago when, if you couldn’t do an integral or a PDE you couldn’t just fire up Wolfram Alpha or Mathematica or Maxima and ask it to do it for you. Best you could do was run over to the library’s Reference Section and pore over a thick dusty Handbook of integrals or tabulated PDE solutions and boundary conditions.
But you are right, a lot of math tools being taught to undergrads are archaic. The Math Departments have been too slow to change.
It’s not about “immunizing” them at all. Teaching math is no magic potion to prevent mistakes.
The more productive way to look at it is whether teaching them basic calculus would help or hurt their toolkit in a substantial way. Fine, if you think it doesn’t help skip it.
Just because engineers still make mistakes & structures still collapse isn’t a good argument to stop making them take mechanics courses, just because “mechanics won’t immunize them against making mistakes”!
There is a big difference between engineering students and social science etc. students in terms of entrance-level numeracy and motivation to study things like calculus. If math is taught to soc sci students forcibly (via the math dept or by whatever other means), they won’t really learn much, they will continue with their cookbook methods esp. if their professors work at the current level of of the field in question.
Also, what proportion of engineers will cause structures to collapse? I doubt that proportion is high, otherwise a revolution would be happening right now in teaching engineers to build stuff.
I agree with Daniel that getting mathematicians to teach math is not a solution, but getting non-mathematicians to take over is also no solution. We need more people like Sanjoy Mahajan, with his unique approach to teaching mathematical concepts. (He is a physicist.)
My solution seems to work at Potsdam. I have a two-stream system. I teach grad level classes in Foundations of Math (teaching the stuff Rahul suggests), followed up by formal/mathematically inclined courses on statistics. That is one stream, and is only for people who can survive the Foundations of Math. The people who took this course seem to be doing really well in research.
The other stream is one introductory level course in stats where I deliver the basic ideas informally, mostly using simulation (Sanjoy Mahajan inspired me a lot over the last year after Andrew blogged on his books, and strengthened my belief that this was the right way). This is for the majority of the non-numerate grad student population and leaves them capable (if they do well in the exam) of correctly carrying out t-tests and fitting hierarchical linear models. I don’t teach Bayes at all in this stream because the goal is to get them to at least do the bare minimum correctly with frequentist statistics, and (importantly) because their own future PhD advisors will probably know nothing of Bayes and will likely react with puzzlement at best when presented with a Bayesian analysis.
BTW, in the stats-lite course I skip ANOVA entirely, but students keep clamoring for it, because even now, in 2016, they mostly see ANOVAs in papers. I stubbornly refuse to teach ANOVA.
It’s hardly lacking knowledge of calculus or linear algebra that causes all the crappy research, as evidenced by eg economics in which the undergraduates have to learn that.
What an brilliant post from Andrew. I agree with you totally. I have never understood how my peers get by without calculus and computational skills. Actually, many of them don’t now I think about it!!!
I think three things need to be added to an already busy curriculum in psychology. The first is that psychologists/social scientists and indeed scientists need to employ professional statisticians to review research. Just as clinicians check their work with supervisors and peers this, IMHO, is the start point for a more tractable set of findings. Second, there is a need to focus on understanding the **conceptual** ideas around and interpreting psychological and scientific results. This is not the same as what nowadays is taught (in NZ, for example, I saw a conference paper where the speaker got the definition of odds ratio wrong — sigh). Most psychologists are math-averse and very very few have formal math/stats training past high school. But this doesn’t preclude understanding of the limits of one’s expertise. My third preference is that ALL science strive to derive an **underlying model**. The example I use is that when analysing signals with noise, the mathematical techniques (fft, convolution) seek a “prior” signal, but that the signal is produced from a known source/model with theoretical parameters. Too often social sciences appear to derive a model from the correlations/effects without any clear theory of how such results might have arisen. Another example of this conceptual failure was in some work I (un)did in forensic prediction where two measures were being used additively, even though they measured the same thing (psychopathy and future offending). Despite me being clear about how even simple Bayesian approaches showed this as invalid, one of the Principal Advisors simply ignored the science. These discussions are fantastic but, sadly, preaching to the converts!
Not wanting to be depressing but I was at a statistics conference recently where very clever statisticians were discussing all sorts of bizarre manoeuvres to get valid p-values out of complex study designs. I just thought: why? The idea that you need to do null hypothesis testing with p-values seems very pervasive.
Simon:
Yup, this is horrible. This sort of thing has been bothering me for 20 years!
My guess is the quantitative stuff will be too hard for them and maybe especially on you (your time and likely lack of productive impact).
Maybe focus on material like what is on http://metrics.stanford.edu/ (especially http://peerreviewcongress.org/index.html ) from social group process perspective. They won’t be able to weigh on the technicalities but they should get some sense of different communities with different perspectives on the value of research currently being done.
Many years ago I had to teach Rehap Med students statistics and the focus on design issues (why to randomize) and especially quality score guides for randomized trials seemed to go over well – the students chose to evaluate their faculties publications for their projects and the highest score was a 3 out 10 ;-)
I like these methodological posts. I cover much of the same material from a different perspective (following Andrew et al.’s paper on multiple comparisons) in a repeated binary trial setting in this Stan case study (also available in an RStanArm version).
Coding’s quick if you know what you’re doing. It’s those known unknowns and unknown unknowns that slow you down (concepts not originally due to Rumsfeld—Rumsfeld got undue grief for stating how engineering project managers have been thinking for roughly forever). For me, that’s inevitably wrestling with R and ggplot2 (often resolved by asking Ben or Jonah something or letting them correct my sub-par first passes) and making sure everything’s terminologically consistent (lots of cross-referencing BDA and letting Andrew correct my sub-par first passes). When we started with Stan, Daniel, Matt and I could barely get complex templated C++ code to compile and spent afternoons poring over error novels that we can now diagnose in seconds. There are algorithms like HMMs I can code in minutes now that took me days the first time I looked at them, and still many many algorithms good programmers can do in minutes that might take me a week on the first go.
Just wondering if you’d say the same about empirical Bayes. I’m using a Bioconductor package that carries out multiple tests (typically tens of thousands), and the process is, colloquially: estimate the many effect sizes frequentistically(!); estimate tau from that empirical distribution; calculate a MAP estimate of effect size and spread (per test); calculate a p-value based on these MAPs; correct these p-values using Benjamini-Hochberg. I’ve occasionally felt uneasy about the presence of both the ‘prior’ and the explicit correction (but even more uneasy of my ability to rigorously argue either way on dropping the final correction). Would be great to hear the view of those whose intuition is more honed than mine in this area.
Gavin:
As I wrote at the end of my post, you can estimate tau from the data. But I’d do it directly rather than messing around with p-values. Really I don’t see any need to compute a p-value at any step in the procedure, from beginning to end.
Perhaps the naive concern:
If the amount of data in a study is so small that the prior becomes important, do we at times run the risk of making the same type of mistakes that occur due to P-Hacking? Now certainly there are cases where it can become just impossible for some parameters being measured to have certain values, but I do have some concern over “the non-informative prior gave nonsense or inconclusive results, let us try a more informative prior”.
If the data itself requires a highly informative prior, does it suggest that the study itself is not adding much value? Perhaps it is still worth publishing, along with providing the data so that it could be aggregated with future studies.
Jon:
Sure, but that’s the point. If the people who’d done power pose or ovulation/voting or beauty/sex-ratio or ESP or all those studies had used reasonable zero-centered priors, they never would’ve made those claims with confidence in the first place. It is the prior information that reveals that, as you put it, “the study itself is not adding much value.”
Statistical methods are often sold as ways of extracting dramatic conclusions from noisy data. But sometimes a statistical method can be useful because it protects a user from making dramatic claims that aren’t supported by the data.
I get the idea of zero-centered priors on many of these issues. But what prior would you use for the speed of light? I might try something like N(3E8 [cm/sec], tau), where lets the prior assume suitable mass across all measured values to date and then some. What would you do? (My copies of your books are currently much further away than arm’s length, but I’m fully expecting “Look on p. X of Y.”)
… where tau lets …
3E8 [cm/sec]
So, SI definitions of the second and the meter are currently given here:
http://physics.nist.gov/cuu/Units/current.html
The second is defined in terms of the frequency of a particular photon emission, and the meter is determined in terms of the distance that light travels in a particular time. This means the speed of light is a fully defined quantity. The only question is given a particular distance, how many meters is it?
;-)
But, taking the general idea in hand rather than the specifics of SI unit definitions, I’d do a similar thing to what you suggest Normal(3e8,3e7) in cm/s would do pretty well if I were planning to use a couple of high precision measurements. If I needed c fairly accurately for fitting a model where I didn’t have direct measurements of c (ie. inferring c from some complex process) I’d probably go look up some results, and provide a more informed prior. In fact, I did something just like that for g the acceleration of gravity near the earth’s surface in a demo-project:
http://models.street-artists.org/2013/04/26/1719/
Oops: leaving out “tau” wasn’t nearly as embarrassing as changing units in mid-phrase. I knew that. Sorry.
Daniel: thanks for the link to your experiment that’s nicely matched to just this question.
@Andrew:
Just like we characterize data as “noisy” is there an analogous concept for priors? Can a prior be “noisy”.
e.g. If on a specific problem I get grossly different priors by asking different experts how do we deal with it & what is the effect on our conclusions? Can this be termed a form of noise or is this something else to be handled differently?
Is there a way to characterize the relative “noisiness” of data vs priors on any given problem?
In your example, priors *are* data, that is you’re asking experts and getting data on what they think the right prior is. It’s a measurement of a psychological state so to speak. So I think there’s no problem talking about those states being noisy when sampled among the population.
I don’t think it makes much sense to talk about a particular single prior specification being “noisy” though.
What bugs me is that we often write / think of a “prior” as a single entity where there exists a plurality just as in measurements and the process of mapping multiple highly different priors to “a prior” seems to be not as much considered in most problems.
We often start with an ad hoc prior but call it “the” prior. I don’t think we would ever just measure one single data point and call it “the measurement”, or even if we took multiple measurements, chose arbitrarily a single value to use in further analysis as “the value”.
But isn’t that what we essentially end up doing with priors?
The question to ask is “what values of the parameter am I willing to entertain?” Any prior that places the set of values that you’re willing to entertain in the high probability region is usually good enough. So for Bill’s example of the speed of light
normal(3e8,3e7) m/s is probably good (actual value technically defined to be 2.9979246e8)
but exponential(1/3e8) is just fine for lots of purposes. Imagine that you have a measurement system capable of measuring to 10% accuracy. After 1 measurement your posterior is going to be +- 0.3e8 so the fact that the exponential prior includes values of 3 m/s out to 9e8 m/s that would still be considered within a high probability region is irrelevant.
The typical problem with experts in a field without high precision information is that their priors are TOO NARROW, and so if you ask several experts you’ll get a bunch of tight intervals that don’t even overlap. The solution is to use a prior that encompasses everything they all say.
What’s the a-priori frequency of failures of space-shuttle launches? The NASA managers said 1e-7, the rocket booster engineers said 0.1, the solution? beta(.5,5) or something thereabouts, or maybe uniform(0,.5) or exponential(1/.05) truncated to 1, or normal(0.05,.1) truncated to [0,1]… anything that includes all the experts favorite regions of the parameter space is reasonable.
My recent set of posts and commentary about Cox’s theorem make it clear, the “correctness” of a Bayesian probability model is a question of whether the state of information it’s conditional on is well summarized by the choice of distributions, not whether there’s an objective fact about the world that you’re trying to match.
Left out the link: http://models.street-artists.org/2016/08/16/some-comments-on-coxs-theorem/
In other words, we acknowledge the noisiness in data & have developed a rich & explicit framework to deal with & and sometimes to map the varied measurements into a point estimate.
But in the case of priors, we seem to not explicitly consider how we get to “the” prior (notwithstanding some work on prior elucidation from expert panels)? Is that reasonable?
This is not how I use priors at least. I always do a sensitivity analysis with different prior specifications to check whether my posterior changes as a result of the prior. After three years of doing this, I have realized that in some of my own datasets (i.e., when I have lots of data) it simply doesn’t matter, I can even use the uniform priors that Andrew now rejects and get the same result. In cases where data is sparse, the situation is completely different of course and one has to proceed carefully and systematically.
Sometimes an informative prior is the proper response to *too much* data. Specifically, if you know that there’s some non-representative aspect to your data, you need to protect your model from having its parameters sucked towards what the data says. Consider the point of Multilevel Regression with Poststratification (MRP). The poststratification step is really asserting prior knowledge about the population (usually from something like a census) to correct biases in your data.
So what does this do with the false discovery rate procedures? Eliminate the need for them?
Actually, now that I think about it, can you actually calculate the FDR probabilities from the Bayesian procedure? You may not be aware but in biology FDR is used all the time due to the large number of gene expression comparisons made from high-throughput sequencing experiments. So this has direct implications for a large number of research projects.
Numeric:
I’ve never looked into it in detail but I’ve always assumed that those procedures can be mapped to hierarchical models—I think Brad Efron has written a bit about this. In the fields in which I’ve worked (social science, environmental science, and some other things), zero comparisons effects typically don’t make sense, so I don’t like the whole “false discovery” framework. It could be different in genomics but even there I suspect it’s not so different as people might think. When I’ve talked with genetics researchers about these sorts of statistical investigations, they’ve described these methods more in terms of “screening” than discovery. I guess what I’m saying is that I’m pretty sure that false-discovery-rate methods have the same sort of adaptive properties as hierarchical models, so that’s good, and I suspect further progress could be made in those areas by moving away from p-values entirely.
>”It could be different in genomics but even there I suspect it’s not so different as people might think.”
It is not at all different. Every gene is correlated with every other gene and affected by every external influence someone would attempt. It is only a matter of your sample size and how strong these correlations are.
I know this is the standard practice, but it’s not what people actually do in biology. Nobody cares about false-discovery rates per se, they only care about ranking the genes (or isoforms or SNPs or whatever) either in phenotype/disease studies or differential expression. Why? Because you get tens of thousands of potential targets, but only have time to run a few followup PCR experiments. So what do they do? They rank by p-values or probability of differential expression. I believe it would be fruitful for them to think in terms of ranking. And how do I know they don’t really care about false-discovery rates? Because they never seem to worry about calibration.
I think what’s really going on in these Biology experiments is an attempt to minimize the cost of finding something useful. A lab wants to discover a gene they can target for drugs to prolong remission of cancer, find out which pathways are involved in recruiting cells for bone repair, detect a cancer before its very advanced, discover how an environmental toxin modifies kidney cells… whatever. They’ve got a large number of genes that might be involved in the process. They have a small pile of money to do research. They need to focus their money somewhere. What subset of “every gene in the genome” should they dump their money on?
Unfortunately for Biologists if they understand anything about statistics it’s what you learn from “Statistics for Biologists 101” which is more or less a t-test and a chi-squared test, so their concept is “there are true targets and there are false targets, and I want to minimize the number of false targets while keeping most of the true targets so that I waste as little money as possible” so they describe this to a classically trained statistician and wind up with FDR procedures.
I think this makes them feel like they’re scientists because they’re “discovering” things, as opposed to engineers who “minimize costs”. But, the truth is, *at this stage in the process* they’re looking to trade off costs vs number of useful results. If they formulated their problem in that way, they’d wind up with a more consistent and logical framework.
But if your cost-per-screening-a-gene is roughly constant won’t the results be roughly the same as what you got from a naive FDR based approach?
Do you have evidence that a nuanced approach gives better results?
It’s not so much the “screening” as the “followup” that’s the costly bit. Screening comes in where you collect all this data that you do the FDR junk on… The FDR junk then gives you a list. How many items on that list should you follow-up? Which ones? All of them? Presumably there is both prior information, as well as “effect sizes” which should be taken into account to determine which are the most promising. None of that occurs in FDR, whose purpose is really just a way of limiting a YES/NO hypothesis testing procedure to produce a more limited number of YES.
In practice, sometimes this step is done where Biologists typically look at these lists and then just select stuff they think looks good (ie. stuff involved in pathways they can imagine being “real”)
It’s making the core concept driving your whole process into a dichotomization that bothers me. There’s a lot more information there.
In general, I often see people critique an existing method on that grounds such as that: (a) it makes ad hoc choices or (b) It involves dichotomization of what is truly a continuous outcome or (c) because it does not use some info that is available & “ought” to be relevant to the problem or (d) because an alternative approach can be deemed “more logical”
My point is the challenger method must show that the improvement (if any) in the final metric of performance you get by removing shortcomings is worth the additional effort.
True, that many areas use simplistic, ad hoc predictive methods that are leaving information unused on the table or have alternatives with richer structure or logical foundations.
But unless the alternative can demonstrate that all its ingenuity can actually translate into better performance, or in fact, performance so much better that it is worth the additional modelling effort & the cognitive switching cost, I think practitioners are entirely justified in sticking to their same, old, flawed boring methods.
There seems to be a lot of effort to do all sorts of sophisticated stuff within the FDR framework. Its hardly the same old flawed boring stuff its like this towering edifice of papers and software packages all designed to solve the wrong problem automatically. At least that’s my impression.
@Daniel
You could be right. I don’t know.
My point is that is I see a lot of arguments claiming superiority of an approach based on the merits of its logical structure and what information it uses than arguments based on the actual performance on outcomes that matter.
>”final metric of performance”
What if the final metric of performance is how many papers you produce, and due to confusion, the limiting factor to publishing papers has become how many “statistically significant” results you can generate?
I think this is what is going on, the way of assessing progress used by many researchers these days is itself fatally flawed. That is exactly why NHST is such a destructive force, it allows you to *think* you are learning something when you are just producing massive amounts of garbage. I am by far not the first to come to this conclusion. It was pretty much Lakatos’ position in the 1970s…:
“one wonders whether the function of statistical techniques in the social sciences is not primarily to provide a machinery for producing phoney corroborations and thereby a semblance of ‘scientific progress’ where, in fact, there is nothing but an increase in pseudo-intellectual garbage…this intellectual pollution which may destroy our cultural environment even earlier than industrial and traffic pollution destroys our physical environment.”
Lakatos, I. (1978). Falsification and the methodology of scientific research programmes. In J. Worral & G. Curie (Eds.), The methodology of scientific research programs: lmre Lakatos’ philosophical papers (Vol. 1). Cambridge, England: Cambridge University Press. http://strangebeautiful.com/other-texts/lakatos-meth-sci-research-phil-papers-1.pdf (pages 88-89)
Anonuoid: I didn’t want to harp on that too much. It is a significant issue though, possibly the single biggest issue in modern academic science.
@Anoneuoid
Sure. If you make no. of papers purely the metric, sure you get truckloads of crap.
But no one’s contesting that. I hope.
This is the point I was trying to make in my comment about ranking and followup PCR experiements. It would be even better to include the costs of followup rolled in the decision. But it usually amounts to the same thing because the followup budgets tend to be pretty fixed (it’s not like they see the results and say, “hey, let’s followup on 100 genes because they all seem like good bets”—they just don’t have the money, postdocs, or time).
And that’s a great use of generics in the statement about “Biologists”! There are lots of biologists who know quite a bit more about stats than that, and many more biostatisticians. The causes for this also involve supervisor and editor pressure to report things in terms of p-values. Mitzi used to work in this area and the editors for a paper she was working on for the ModEncode project for Science insisted that they provide p-values for their exploratory data analysis (which involved a clustering model nobody believed was a good model of anything, but useful for exploratory data analysis).
There is SO much effort put into these various packages on bioconductor and soforth, a bunch of smart people who seem to be led down the garden path here. Commercial and open-source projects for lots of really complex canned analyses with little web-based dashboards for point-and-click implementation of the garden of forking paths.
Typical bench Biologists really don’t know much more than a t-test and a chi-squared in my experience. There are more specialist people who call themselves Bioinformaticists and of course there’s Biostatisticians neither of those groups would typically have the skills to say do sterile tissue culture, or debug PCR primer problems, but their level of statistical sophistication is much higher. So it’s a matter of specialization. Bioinformatics/statistics seems to be predominantly about fancy methods for adjusting p-values though. The whole framework is about “there is an effect” vs “there isn’t an effect”. I’ve even had biologists *explicitly* tell me “I don’t really care whether it’s big or small, just whether adding hormone X produces a difference” or the like.
An effective counter to the “is or is not a difference” is to ask them whether “do you care if adding hormone x produces 1 extra transcript per decade?” Part of what’s going on is that there’s so much noise in Biology that if you find an effect, the effect is usually big enough that it’s practically significant (2x or 5x the transcript rate for example) of course, as Andrew’s regularly pointed out, type M errors are very common in p-value driven “discovery”
I’ve watched my wife working with these canned packages… click here to select from normalization method Foo, Bar, Baz, Quux each one linked to a particular paper advocating for one vs another. Then run an enormous least-squares based ANOVA of 20,000 dimensions, you can choose from taking the logarithm of the data first, or doing some other nonlinear transform, or just doing the raw data, you get 20,000 p values, you can use 1 of 15 different FDR correction procedures, get a principle component analysis, sort by post-FDR p value, sub-select by gene ontology group…
Does the user have ANY idea what any of it means? When I ask my wife she gets really frustrated, because she’s basically just doing what someone told her to do. In the end after making 10 or so ad-hoc choices are you discovering anything, or just finding data to justify your preconceived notions, or maybe just arriving at a puzzle-solution to get past the grant/publication gatekeepers?
I remember it being really common to threshold on effect size (usually an effect size of at least 1 in log2 space, so 2x/0.5x) in addition to FDR, at least back in the microarray days.
This is what I was trying to query in my previous comment. The R package I’m using does something similar to Andrew’s approach, shrinking the effect size towards zero, but then does an additional round of FDR, and I worry that this might introduce some form of double jeopardy so, inspired by this post, I intend to run a few simulations.
We (I’m a maths guy, pretending to be a statistician, advising bioinformaticians how to help scientists) tend to use FDRs in Andrew’s screening sense, where we threshold on a fixed FDR, and then rank on (if anything) effect size. But more commonly the hits are then taken as the starting point for the scientist building a narrative, and performing more focused experiments.
I was wondering what you would do about multiple testing in a “garden of forking paths” scenario where you have several analyses, but they are not on different independent datasets? I’m currently working as a statistical consultant on a behavioural economics project where it was hypothesised there would be an effect of some government policy intervention on a range of health outcomes. We did a regression discontinuity design and we found no strong evidence of anything (statistically insignificant and widely varying results), so we weren’t going to even bother thinking about multiple comparisons.
But my clients want to write this up as a negative result, and so they should. So, with the intention of showing we have been thorough, and not with any intention of p-hacking, and because we really didn’t have any strong beliefs on various analytical decisions we had made, we redid the analysis with a range of “garden of forking paths” style tweaks to the sample selection, the bandwidths, covariates etc. Now we have a couple of hundred estimates on the same dataset, and they are very noisy, with different signs etc. Inevitably a couple of effects have significant p-values.
What would be the proper way to approach this? It doesn’t seem to fit into a hierarchical framework.
Mat:
Long answer, I’d fit a multilevel model. Short answer, I’d take what you did already and call it a multiverse analysis as in this paper (which I guess I should blog sometime).
If you want a single p-value, I recommend taking the mean of the p-values from all the different analyses you did.
Thanks for the link. That “multiverse” idea really taps into the problem, and it would be great to see a blog on this. The thing about the “garden of forking paths” and multiple comparisons is that in some contexts applied researchers get the impression that being thorough is good practice – such as, for example, robustness and sensitivity analyses after finding an effect. At other times the message seems to be, “make one choice at each decision point, before seeing the data, or you’ll be guilty of p-hacking”.
My personal preferred practice when faced with what you call “whimsical” decisions is to code up a loop and try every combination. But then, having obtained all this data, there doesn’t appear to be any widely recognised statistical way to analyse and report it. Model averaging??
“Any sufficiently complicated C or Fortran program contains an ad hoc, informally-specified, bug-ridden, slow implementation of half of Common Lisp.” — Greenspun’s Tenth Rule of Programming
Which is to say, aren’t you basically reinventing an ad-hoc version of a Bayesian analysis? The core concept of a Bayesian analysis is basically this: “Here’s a bunch of different possibilities I’m willing to entertain, and some data, which of these possibilities should I entertain after I’ve seen the data?”
The ABC version of how Bayesian analysis works is “pick values from the prior distribution, compute the consequences of the model, and weight this consequences by the likelihood of the error you see between the computed consequences and data” which is to say that ABC looks a lot like “try this out and see how it works, try that out and see how it works, try this other thing out and see how it works…”
So, you have some kind of time-series of health outcomes, and a policy change-point, you have various ideas about how to describe the data itself (reasonable bandwidths to get summary statistics or whatever), and various ideas about how the summary statistics should change post-policy-change (broken-stick linear models, exponential decay to a new stable state, an initial confusion causing worse outcomes followed by a decay to a new stable state where things are better, nothing happens at all post change…)
Take your existing set of analyses as a kind of model-search, incorporate all the model-search ideas into one Bayesian model, put broad priors on it all, run the Bayesian machinery, and get a posterior distribution over what seems to be true.
I agree in principle that we should approach these analytical decisions where possible as an opportunity for continuous model expansion. It very quickly gets computationally infeasible though. It all depends what model of Bayesian machinery you have though, I guess.
No question that very large models that are mixtures over multiple plausible explanations and etc etc are computationally challenging. Thinking about your situation and trying to come up with one model that incorporates many possibilities while remaining tractable can help.
If you’re talking about time-series regression with discontinuity, you might find my recent post on placing priors on functions interesting:
http://models.street-artists.org/2016/08/23/on-incorporating-assertions-in-bayesian-models/
You could, for example, compute some summary statistic of the function behavior in the vicinity of the change-point, and assert something in the model about its plausibility. For example, abs(f(somewhatafter)-f(atchange)) ~ gamma(a,b) to assert that you think there should be on average a nonzero slope up or down in this region, where you choose a,b so as to constrain the slopes you’re entertaining.
You could do a similar thing for the endpoints of the time interval. Calculate a mean value pre-policy, and calculate a mean value in the asymptotic far-post-policy time period, and assert something about the plausibility of the change in asymptotic behavior.
Often this kind of very flexible model can be a substitute for a discrete set of plausible simple models. I mention this, because I recently tried to generalize the state-space vote-share model that was posted a couple weeks back using a Gaussian process, and found it computationally infeasible for 400+ days of data. Looking for a way to specify time-series function behaviors other than Gaussian processes led me to the suggested idea.
Thanks Daniel, I’ll take a look at that link.
Yet another generic that’s nowhere near universally true. Ironically, all the “pure” functional programming languages wound up adding imperative features (for example, Common Lisp) due to the cost of random access in pure functional programs. So you get this motivation for “pure” functional programming, then you go and write quicksort anyway. That’s just how programming goes. You often get the same thing in stats—lots of Bayesian handwaving, then a bunch of point estimates.
When I was at Carnegie Mellon and Edinburgh, I used to work on logic programming (and some functional programming). It used to drive me crazy when people referred to Prolog as a logical programming language. It was basically depth-first search with backtracking (unless you used cut, which was neccesary for efficient non-tail recursion) and if you weren’t aware of this and didn’t code to this, your Prolog programs were doomed. (O’Keefe’s Craft of Prolog remains a great programming book, as does Norvig’s book on Lisp.)
I don’t think Common Lisp was ever supposed to be “pure” it was just supposed to be designed to handle a really wide variety of stuff at the language level. Whereas, in the FORTRAN and C world all that stuff is handled at the library level and therefore re-implemented by each project in a buggy way.
But, fair enough. I’m being perhaps too glib.
Though, my point wasn’t really that Bayes was “more pure” just that when you don’t have Bayes available, a lot of what people do looks like “reinventing” it, just like when you don’t have hash tables in your language, a lot of what people do is write an ad-hoc informally specified hash table library. The history of Common Lisp, Perl, Python, R, Ruby, Lua etc is that we get closer to just having all that stuff built-in. That’s also the history of BUGS, JAGS, Stan
Having done a bunch of Prolog programming back 15 years ago, I honestly think that Stan feels like Prolog at a certain level. Prolog is a method for specifying depth-first-searches through discrete spaces, Stan is a method for specifying Hamiltonian searches through continuous parameter spaces. If you don’t acknowledge the search mechanism you can be doomed in ether one.
A Prolog program basically says “find me values of variables that make certain statements true” and Stan basically says “find me values of variables that make certain statements plausible”
My point exactly. The functional programming wonks tend to extoll the purity of functional programming, but then wind up using languages with side effects like Common Lisp. Same way people extoll the virtues of Bayes (consistency, taking into account posterior uncertainty in inference), then fit models using variational inference and perform inference with the point estimates. I’m not saying that’s a bad way to go in either case if you want to get real work done (and as an aside, I think the focus on getting practical work done rather than scolding everyone for doing things wrong is why machine learning is eating statistics’ lunch). The pure solutions are often too burdensome.
I also think it comes down to “horses for courses” as the British say. There are better matrix and math libraries in FORTRAN than in Common Lisp. And better internet libraries for things like unicode and sockets and threading in Java. And C++ has both everything and the kitchen sink in the language *and* in the libraries. It’s enough to make a programming language theorist like me cry.
I honestly don’t know what the functional programming languages are good for. I love them dearly as theoretical constructs (I used to do programming language theory and a lot of typed and untyped lambda calculus), but I’ve never run across a practical problem where they made a lot of sense. Part of that’s just the lack of large communities of programmers in fields I’m interested in.
What I miss the most from the functional programming languages is lambda abstraction. It’s a complete hack in C++ with bind, functors, function pointers, etc. and also a hack in Java, too (like functors in C++, but maybe they’re anonymous). You get some of their benefit with continuations in languages like Python and R and even in C++ you can code things in a continuation-passing style (sort of built into my brain after all that Prolog tail recursion).
Guaranteed, though, no matter what language you choose for a project, a chorus of naysayers will tell you that you should’ve chosen another one. My experience at Julia Con was everyone telling me we should’ve coded Stan in Julia!
@Bob
Great points.
I’ve found the size, activity and expertise of the user community is a HUGE factor in how useful a language or package turns out.
>>>but I’ve never run across a practical problem where they made a lot of sense.<<
Lisp was used in AutoCAD and Emacs. Dunno if it meets the approval of functional purity.
@Rahul, it’s not clear to me if Bob considers LISP within the scope of what he’s talking about when he says “I honestly don’t know what the functional programming languages are good for”. I think he might be referring more to things like Haskell where there really *are no* side effects (ok, technically what there is is a state that you pass in and then a new state comes out).
Common LISP is *not* a pure functional language. it’s got all kinds of looping and iterative constructs, setf to set the value of just about anything, lots of printing and formatting stuff, explicit file-IO mechanisms. But, it’s cognitively very different from other languages. One big reason is the macro system where the language itself is used to write new language constructs.
LISP’s biggest problem seems to be that it just requires more than a High School education and a “learn X in 24 hours” level of knowledge in order to hire someone to do even basic work on a LISP program. For example, NASA hired some great programmers who came up with some kind of fancy autonomous robot planning and execution software which was fantabulously effective at what it was supposed to do, won some award, and then was canned by JPL. One big issue is no-one cheap could work on it. Same thing happened to Yahoo Store (programmed in LISP, bought out by Yahoo, then re-built over a decade in C++ by which time Yahoo had pretty much crashed and burned but just didn’t know it yet)
http://www.flownet.com/gat/jpl-lisp.html
I really want Julia to take-off, but I won’t be switching over until a very extensive version of ggplot2 is available ;-) and that gets right at your point about the extensive user community.
>”we found no strong evidence of anything (statistically insignificant and widely varying results)… Inevitably a couple of effects have significant p-values”
This is strange to me. This comment seems to say that statistical significance means finding strong evidence (it doesn’t) but also realizes that statistical significance is just something inevitable that happens by looking at some data.
No, I just was trying to find a shorthand way to say that after looking at the results we changed our belief to “there doesn’t appear to be anything going on here, or at least our data isn’t good enough to estimate it (and we have pretty good data)”.
I’m using hypothesis tests and p-values to go with the flow, because it’s not my project.
I think this paper by Simonsohn et al. may be helpful:
http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2694998
Yes, really good paper. There’s a phrase in the paper that sums up the difficulty for me: “the specifications are neither statistically independent nor part of a single model”.
Perhaps in principle we can write a bigger model that all the specifications fit into, but in practice it quickly becomes impossible. Even multilevel models, to handle different subgroups of the data, can be computationally prohibitive if we already have a highly parameterised model. So it’s good to have people thinking about how to perform inference in the presence of methodological ambiguity.
theta <- rnorm(N, 0, tau)
Shouldn't tau be tau^2?
Sean:
No, R (and Stan) parameterize the normal in terms of location and scale.
What does Occam’s Razor say about this? It is more likely to get just the likelihood correct, or the likelihood and the (one of of infinitely many possible) prior correct? How about for multidimensional problems?
Justin
Justin:
Here’s what I think about Occam’s Razor.
Great intuitive post. I also read your paper “why we (usually) don’t have to worry about multiple comparisons. I’m an applied statistician with MS level classical training in statistics. I’m trying to steer away from using frequentist methods towards bayesian inferences, but there are situations where I’m quite lost.
I work in an industry where 2-factorial ANOVA experiments are common. For example, we’re testing 6 oils with 6 seals for a total of 36 ‘treatments’ in 2 blocks (so 2 replications, one in each block). In a typical frequentist scenario, we’d fit a linear model with fixed effects for Oil, Seal and Block plus an Oil:Seal interaction (as we believe oils behave differently at different seals). The typical procedure in a frequentist scenario is an F-test followed by Tukey pairwise comparisons.
I’m having a hard time building the blocks of this model in a bayesian context. How do I prevent the mutliple comparison here?
1. According to the post, as long as I have somewhat informative priors, we should avoid that problem. This is in itself a daunting task. I or the subject matter expert can’t tell me what they believe about each interaction coefficient. From the paper I referenced, the solution is to then build a multilevel model.
2. Do we then treat both factors, oil and seal as random effects? If we’re interested in making statements only about oils, do we then treat Oils as a random effect and seal and block as fixed effects? I’m finding it hard to build an intuition of this model and be able to justify the choice of priors and or random/fixed effects.
Hoping this gets some attention and discussion!
Dilsher:
To start, I’d take a look at what we do here. I’d start by fitting the model using stan_glmer in rstanarm in R (or glmer in lme4 in R, if you prefer) with varying intercepts for all batches of main effects and interactions of interest. No F-tests, no pairwise comparisons; just estimate everything.
Thank you, Andrew. That gives me a lot to think/read about. Hopefully I’m able to grasp this concept enough to convince my department to do the same.
I’m having trouble following the simulation that Andrew did. I see code for one instance but not code for how the 1,000,000 repetitions were done.