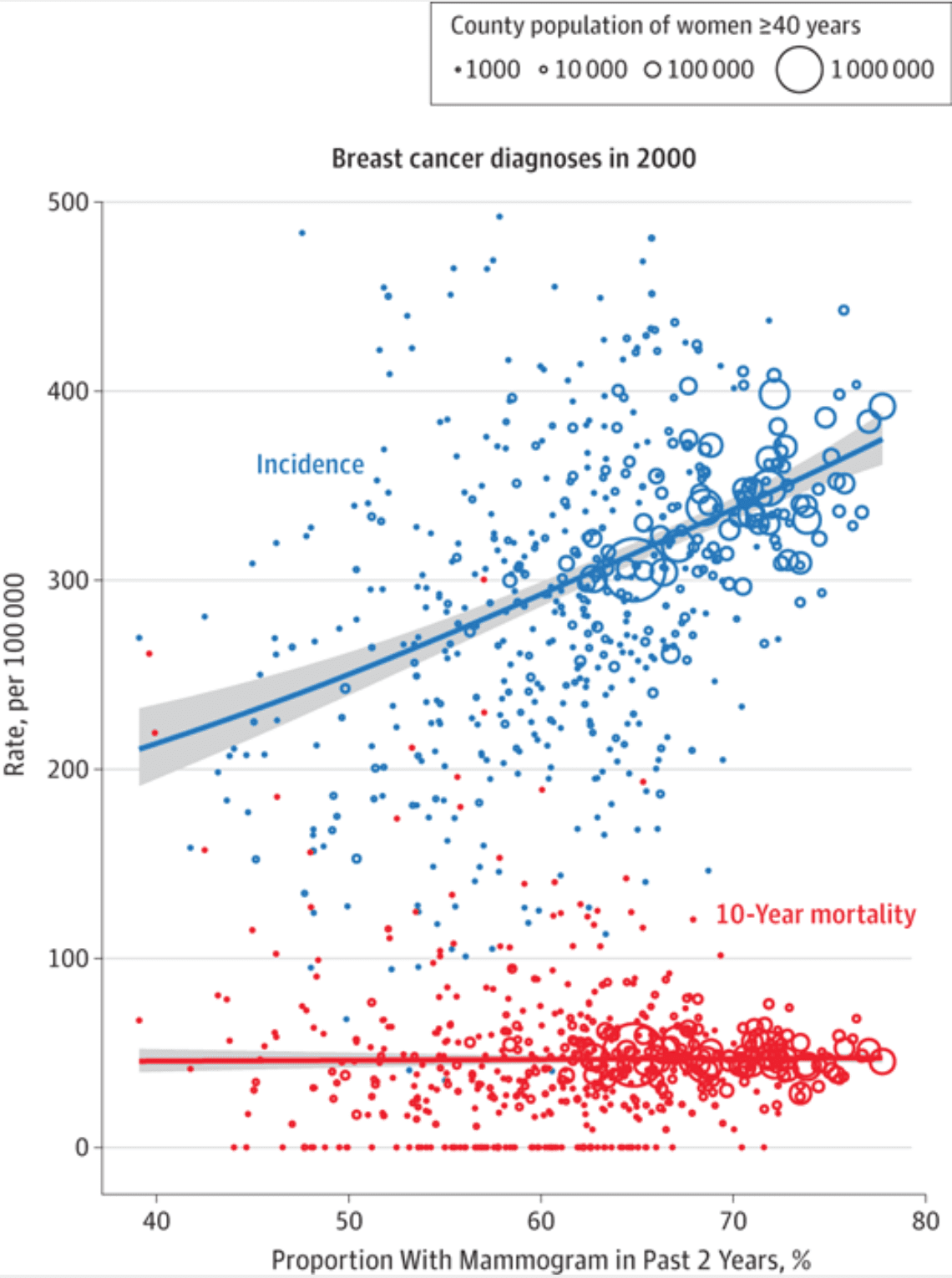
Paul Alper points me to this article, Breast Cancer Screening, Incidence, and Mortality Across US Counties, by Charles Harding, Francesco Pompei, Dmitriy Burmistrov, Gilbert Welch, Rediet Abebe, and Richard Wilson.
Their substantive conclusion is there’s too much screening going on, but here I want to focus on their statistical methods:
Spline methods were used to model smooth, curving associations between screening and cancer rates. We believed it would be inappropriate to assume that associations were linear, especially since nonlinear associations often arise in ecological data. In detail, univariate thin-plate regression splines (negative binomial model to accommodate overdispersion, log link, and person-years as offset) were specified in the framework of generalized additive models and fitted via restricted maximum likelihood, as implemented in the mgcv package in R. . . .
To summarize cross-sectional changes in incidence and mortality, we evaluated the mean rate differences and geometric mean relative rates (RRs) associated with a 10–percentage point increase in the extent of screening across the range of data (39%-78% screening). The 95% CIs were calculated by directly simulating from the posterior distribution of the model coefficients (50 000 replicates conditional on smoothing parameters).
Can someone get these data and re-fit in Stan? I have no reason to think the published analysis by Harding et al. has any problems; I just think it would make sense to do it all in Stan, as this would be a cleaner workflow and easier to apply to new problems.
P.S. See comments for some discussions by Charles Harding, author of the study in question.
Properly fitting messy data is of course one of the primary interests for (Andrew and) many of the participants in this blog. So is interpreting data, messy or otherwise. Assuming the calculation for the fit is reasonable, here are two contrasting ways to look at what the data set is telling us:
1. “[T]here’s too much screening going on” because mortality rate remains constant despite the costly and possible harmful interventions.
2. Reverse causality: screening intervention has kept the mortality rate from rising.
Breast cancer incidence and mortality is far from the only cancer which exhibits this type of graph. An outstanding example is South Korea’s meteoric rise in thyroid cancer:
https://cdn2.vox-cdn.com/uploads/chorus_asset/file/3848460/thyroid_chart.0.jpg
There are some issues other than fitting concerning the breast cancer graph which are discussed in
http://www.healthnewsreview.org/review/effectiveness-of-breast-cancer-screening/
In particular, “The research study used ecological observations of large groups (not individuals) that are subject to inherent biases.” The large groups were 540 counties in the U.S. The so-called “ecological fallacy,” a seductive fallacy if ever there was one, is described with examples in
https://en.wikipedia.org/wiki/Ecological_fallacy#Individual_and_aggregate_correlations
I remember a similar story a few years ago about how towns in the US were spending more every year on firefighter’s in spite of the fire damage / casualty rate steadily declining every year.
Causality is a tricky thing.
Yes, but here’s a case where nothing is happening in the cancer rates. Is it really that credible that cancer death rates would be growing extremely rapidly without intervention? And then there’s the model in which there’s a clear causality for increased screening… increased billing!
So, while I’m willing to withhold final judgement, I’m also willing to say that the most likely way this works is that doctors screen more in hopes that it helps, and with knowledge that it certainly helps the dollar-flow… and yet it doesn’t do much medically.
” Is it really that credible that cancer death rates would be growing extremely rapidly without intervention?”
To some extent it is. If you look at breast cancer incidence and mortality rates back in the 1950-1980 era, before there was widespread use of screening and before modern treatments for breast cancer were available, you see that both were, in fact, rising rapidly (even after age adjustment).
While it is hard to believe that the rapid rise seen back then would have continued unabated several decades later, it is plausible to believe that these rates might still be increasing were it not for interventions.
There is a major, and rancorous debate in the breast cancer control community (sometimes spilling over into the lay media as well) over to what extent screening actually leads to reductions in breast cancer mortality and to what extent it just leads to overdiagnosis of lesions that would never appear clinically without screening. Many modeling groups have grappled with this question, and, unfortunately, the answer depends on assumptions about unobservable effects (secular trend in breast cancer incidence in the absence of screening, proportional incidence of non-progressive small breast cancers, distribution of the duration of the pre-clinical state for progressive cancers). While fitting models to observations of incidence and mortality does constrain the joint distribution of these parameters, the data available do not identify them individually. And the various combinations of assumptions about the unobservables that are compatible with the observed incidence and mortality lead to very wide variation in estimates of overdiagnosis. (Published estimates of overdiagnosis rates are even further confused because different people define the numerator and denominator differently–but even when recast to a single definition, the rates vary markedly.)
While one can propose an epidemiologic study that would settle the question definitively, it is not something that would be feasible due to large numbers of women who would have to be followed for life. Moreover, it would involve random assignment to screening or no-screening which, in the minds of some, would be unethical. This study will never be done. Real evidence may emerge from ongoing studies in which women with very small, early lesions detected on mammography agree to be randomized between immediate treatment and active surveillance (frequent follow-up imaging studies to look for progression of the lesion, and deferring treatment until that occurs, if it ever does). It is also possible that a biologic basis for distinguishing potentially progressive breast cancers from non-progressive ones will be found–but that seems a more remote prospect at this time.
Let me ask you this. What are the constraints on how many cells of each type are there per gram of breast tissue and how often they divide normally? What are the constraints on rates of indels, point mutations, and chromosomal missegregation per division for each cell type?
From my reading of the cancer literature, I doubt there are useful constraints available on any of these basic parameters. If I am correct on that, I think it is an exercise in futility to attempt figuring out what is going on until we get that information.
If I am wrong that this crucial data is missing, I’d be very interested in the relevant literature.
Note that the chart doesn’t show the evolution of incidence and mortality over time, but across counties. Maybe the counties with a higher proportion of mammograms would show higher mortality if the extra mammograms were not done. But the explanation will not be as simple as an underlying rising mortality rate cancelling out the benefits of the increase in mammograms.
Ah thanks. I looked too quickly at the graph, and its x axis mentions “years” so I was thinking through time. Instead this looks like a particular time window, and then looking spatially across different regions with different percentages of screening. With that being the case, it suggests that as we sit right now, plenty of places have low breast cancer deaths even without additional screening beyond some base level (around 40% at the left side of the graph). So this suggests either that screening increases in areas where people are more likely to die from breast cancer, and the increased screening then cancels out the likelihood of death across SPACE, or screening buys nothing.
I doubt very much that people are screening more in county A because they know that more people get and die of breast cancer in county A… more likely just that richer people get more screening and it does nothing for them on average.
Possibly a trend in the base-rate of screening is through time keeping the rate of deaths at bay… but this data doesn’t address that at all.
Regarding point 1: It would be quite interesting if this data could be break down by different age groups. Screening for breast cancer is unlikely to be benificial for people with a relatively low life expectancy. So for instance, if a woman is expected to live until age 80, you shouldnt be screened after 75, etc.
I agree — it would be interesting to look at different age groups, both because of the point you raise and because women younger than 40 are sometimes screened too, even though that is not recommended for women of average risk.
I hope to be able to look at this at some point. The data source in the above paper doesn’t include screening rates for different age groups, though, so a new study and approach would be needed. Data limitations are a huge problem in this field.
Paul, thanks for bringing up the paper, and for your comment too. As an author of this study though, I can’t help myself from suggesting that your blog’s readers consider the paper itself (and supplemental appendix!) rather than summaries from the media. There’s more than the one figure :)
Some examples showing non-parametric or gam type smoothers would be great. I think people end up fitting these with finite mixtures, but it’d be great to have some more flexible examples.
“as implemented in the mgcv package in R”
The stan_gamm4 function in rstanarm can do spline stuff if anyone wants to try. We haven’t implemented out-of-sample posterior prediction yet though.
Is the ten-year window far enough out that there’s no point in doing a survival-analysis-style analysis? That is, the casual observation of this casual observer would be that the length of survival makes a difference.
If you’d like to try to conduct the analysis in Stan, let me know. There are some restrictions on distributing the data, but I can see what I can do.
I thought I’d try to get the analysis you suggested running with rstan_gamm4, but didn’t succeed (in addition to no out of sample posterior prediction, the negative binomial distribution may not be supported yet?). Nonetheless, it was interesting to work with rstanarm and shinystan. Nice combination.