
Rasmus “ticket to” Bååth writes:
I heeded your call to construct a Stan model of the height of Kit “Snow” Harrington. The response on Gawker has been poor, unfortunately, but here it is, anyway.
Yeah, I think the people at Gawker have bigger things to worry about this week. . . .
Here’s Rasmus’s inference for Kit’s height:
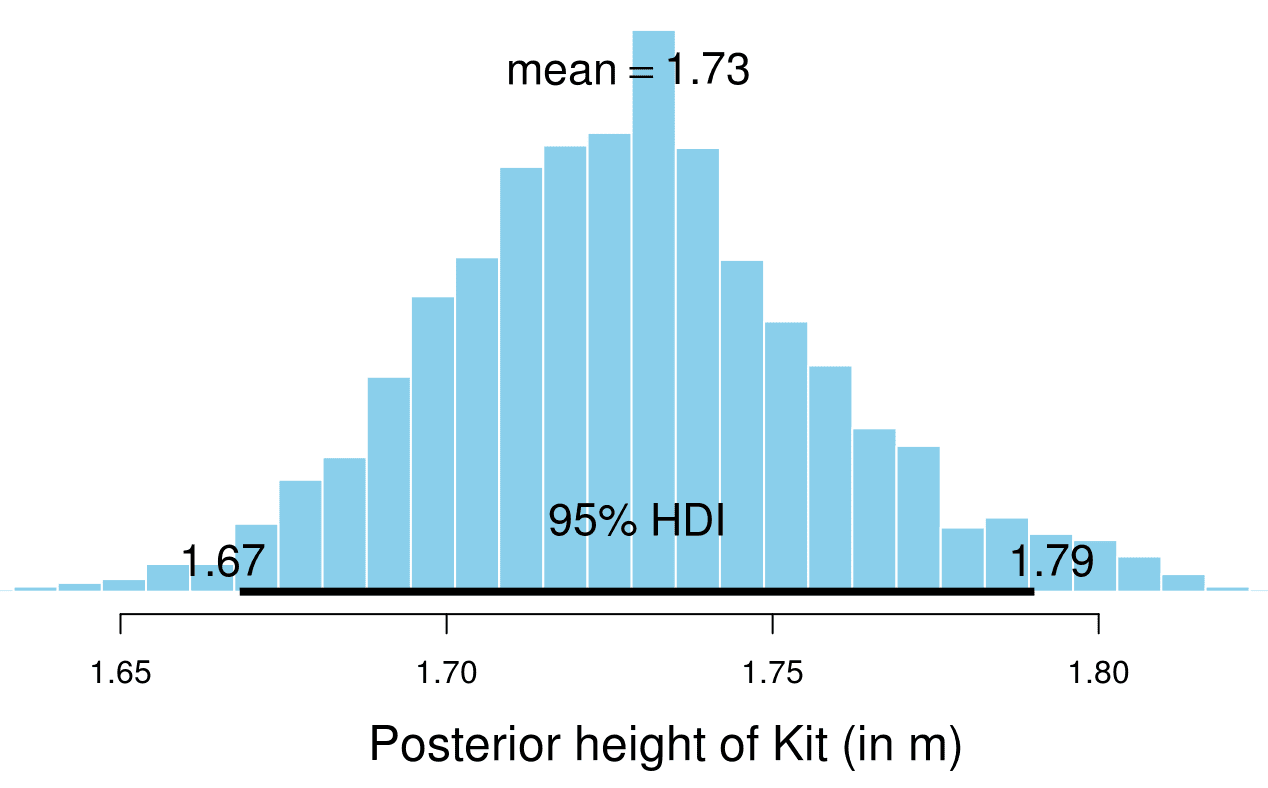
And here’s his summary:
From this analysis it is unclear how tall Kit is, there is much uncertainty in the posterior distribution, but according to the analysis (which might be quite off) there’s a 50% probability he’s between 1.71 and 1.75 cm tall. It is stated in the article that he is NOT 5’8” (173 cm), but according to this analysis it’s not an unreasonable height, as the mean of the posterior is 173 cm.
His Stan model is at the link. (I tried to copy it here but there was some html crap.)
Where does pixel_in_m get its bounds etc?
The pasted code in the post above seems to have lost all “less than” and “larger than” signs, and everything in between. The original model still has them though: http://www.sumsar.net/files/academia/analysis_of_the_height_of_kit_harington.html
Rasmussen: “there is much uncertainty in the posterior distribution”
Relative to what? A 95% PI of 10cm seems pretty reasonable considering the evidence at hand.
I was thinking relative to how sure we would like to be about somebody’s height. I think ideally you would like to state the number of inches with certainty.
Yes but old Kit Harrington is likely to be a few cms shorter than prime-time Kit Harrington. Just as young Kit Harrington was most likely (unless he emerged from the womb fully formed) shorter than prime-time Kit Harrington. Add in shoes and posture (as you did in your model) and height becomes less of a “fixed, true unknown.”
What is height, really, but a socio-spacial-temporal construct? What does it even mean to say ‘Kit Harrington is 5 feet 10 inches tall’? That someone told him to take off his shoes and socks and then they measured his height with a measuring tape? If Kit Harrington had been a baby, that measurement would be different. How different, and why? Just how tall is baby Kit Harrington? These are the truly important questions.
There’s a typo in Rasmus Bååth’s summary: I’m almost certain Mr. Harrington is more than 1.75 cm tall.
p < 0.05
What is the typo? I can’t find it… :/
Ah, yeah… ok… found the typo. Yes he is certainly more than 1.75 cm tall… unless Melisandre puts some strange lilliput spell on him and turns the next season of Game of Thrones into some fantasy version of Ant-Man. :)
I would just like to add that this was more an exercise in trying to come up with something using the given data. It would of course be possible to try to do some kind of meta-analysis of all the verbal reports over at http://www.celebheights.com/s/Kit-Harington-47806.html . But then, who cares really? :)
Rasmus,
I really love this example. It’s clear every distribution represents uncertainty, which is then being aggregated to get the estimate+uncertainty in the one number you care about (height). There’s no hope of claiming any of these probability distributions are frequencies.
If a frequentist rejected the use of probability theory for this example and instead conducted a sensitivity analysis varying all inputs by the same amounts as the variances of your “priors” they’d get essentially the same answer as your posterior.
It would be interesting to get a die hard Frequentist in here to explain to all us why this is hopelessly incomprehensible philosophical nonsense that can’t possibly say anything objective about the real world. Really, I’d pay good money to hear them explain this one away.
@Rasmus
Was this modelling exercise strictly open loop? i.e. Did you get this distribution without tweaking any of the priors, constraints etc.?
I didn’t spend too much time on this model, so no iterations or tweaking whatsoever. Just used some priors that I thought were reasonable and then I pressed the big magic Stan Button. (and then I got some syntax errors, and then I fixed those, but after that it compiled.)
Have you considered that both women are wearing heels?
Jp:
From Bååth’s model:
I didn’t check to see how heel height was used in the model beyond Professor Gelman’s code snippet from from Bååth’s model. As a pointer for future use, do be aware that women’s heel height is not a one-to-one correspondence with increase in measurable height. I was dismayed to find that four inch heels do not make me four inches taller, but rather, between two and three inches at best. There are a variety of reasons for this, but the most commonly occurring (depending on the shoe) is that heels elevate the heel only, not the entire foot.
Obviously, I have a lot of experience wearing ladies footwear.
And I must confess my utter ignorance regarding heeled footwear, male or female. I know the names of at least a doze different kinds of edible mushroom, so that’s something, at least…
As always, I recommend the fanatics at CelebHeights.com for informative crowdsourced arguments over how tall celebrities are. Especially useful are the reports of people who were in line behind celebrities (cough, Alec Baldwin, cough) at TSA checkpoints who get to see them with their shoes off.
I like your model and results, and I’m curious. You seem to be assuming that all three are in the plane of the page. Looking at shoulders and arms, is it possible that their plane is at a small angle to the page?
Yeah, I was considering including a rotation of the view in the model, but (1) it is really difficult to see the angle in the image (2) I would have had to define rotation matrices in STAN and it would have been a bit overkill so… I instead I include the uncertainty regarding the photo angle in the catch-all error term. But feel free to improve the model :)
who are those people?!
Beats me. Some kind of models or movie stars? The background and the magazine in the hands of the person on the right says “Elle” so models seem likely.
You know nothing, X.
(Google “you know nothing” for the reference)
He knows the reference.
Thanks, Corey, for the pointers: I indeed started reading Martin’s books when A Game of Thrones appeared, circa 1996. But I never paid attention to the actors of the series so the names did not ring a bell, while seeing them in (this) period costumes did not click either. So you’re right, Michael, I know nothing!
I know less than nothing, as I am not familiar with the people in the photos NOR with the television show, Game of Thrones. I read some George R. R. Martin short stories in science fiction/fantasy anthologies. So that means that Xi’an knows more than I do.
They are some of the actors starring in the pretty popular show Game of Thrones based on the books by . Kit Harington has one of the leading roles and if you google “John Snow” you’ll get pictures of him as his on screen persona.
I know this isn’t supposed to be serious, but I’m somewhat puzzled by this whole exercise. If I:
* ignore distributions and uncertainties,
* ignore the ensemble of Irishmen and their heights,
* use the “known” heights of the two women (http://jezebel.com/serious-question-how-tall-is-kit-harrington-1711475702) with the assumption that they’re wearing heels that are 2” taller than Mr. Harrington’s, and
* draw some lines on the image to show the vanishing perspective and estimate its distortions (the most important part!) (http://imgur.com/9Jgp3gf)
..I get a height for Mr. Harrington of about 158 cm (5 feet 4 inches). (I can write more detail if anyone wants). This is well outside the confidence interval of the model given above (95% btw 1.67 and 1.79 m).
As hokey as it is, I would bet more on my height estimate than the full statistical model above, which, to me, looks like a complicated way of stating that Kit Harrington’s height is probably like that of the average Irishman, with a little bit of a modification.
Of course, I realize that the point of this fun STAN model was simply to illustrate how simply one could implement this sort of MCMC calculation in STAN. However, it’s perhaps worth keeping in mind that it’s very easy to feel like one has learned more from a model than one actually has, and that things like “# Prior on the measurement error,” aren’t totally obvious.
I sort of regret spending time on this, but I was thinking of sending my students to this page, since we were discussing MCMC today, and I couldn’t stop myself from actually thinking about the image! I refuse, however, to look up who these people are…
Raghuveer:
Three things. First, if you want a simple and accessible example of the applied use of Stan, I recommend you point them to our World Cup analysis (search this blog for World Cup and you’ll find the two posts). Second, the Stan model given above does not ignore distributions and uncertainties, nor does it assume the women’s heels are 2 inches taller. Third, and most important, the point of the Stan model here is that it is expandable: it is in fact very easy to take the existing model and add whatever additional information you have, including the distribution of heights of Irish men and any information you have on the perspective in the photograph. That’s one of the major advantages of this sort of Bayesian model, particularly as implemented in Stan: you can keep adding information.
Raghuveer:
Sorry, I realize I misunderstood your comment, which was that you could get a different estimate ignoring all the distributional information.
So let me rephrase my response.
First, for your students I still recommend the World Cup example.
Second, I think the right thing to do is incorporate all relevant information and uncertainties. Thus, include the distribution of men’s heights—this is the “base rate” and is in fact highly relevant to this sort of inference—and include uncertainty about heel heights, etc., and also include the information that you want to include from the photo. The point is that uncertainties are crucial when combining apparently discordant information. Of course, for this silly problem of Kit Harrington’s height, who cares? But consider it as a simple example of more general inference problems, a way to combine different sources of information in a smooth and flexible way.
Andrew:
Thanks; Looking at it, my writing is harsher and less clear than I intended, which I will blame on being annoyed with myself for spending time drawing vanishing point perspective lines on pictures of celebrities.
I certainly agree that “the right thing to do is incorporate all relevant information and uncertainties.” If I were doing this more thoroughly, I would of course use the (important) uncertainties associated with the perspective estimate, the distribution of men’s heights (though I will admit I’m still a bit unclear on how to incorporate this), etc. I think we’re all in agreement that this would be the best thing to do. I do think, however, that “incorporate” is a tricky word — the simple STAN model does “incorporate” the distortion of the photo with a simple guess for its uncertainty; it’s this false sense of assurance that I worry about. I also don’t mean this as a criticism of the model’s author — I realize this is just a bit of entertainment, and I’m glad he took the time to pounce on this and put something interesting together! (I also notice that he referred to the perspective distortion in a comment above.)
Raghuveer:
To me, the key is to clearly express what information is included in the model, then in future iterations more information can be included.
I don’t know anything about Kit Harrington’s height, but I love Sophie Turner and she is dating Joe Jonas. (https://www.allherboyfriends.com/sophie-turner-boyfriend-dating/)..By the way Sophie Turner’s height is around 5′ 9”.