Aki, Jonah, and I have released the much-discussed paper on LOO and WAIC in Stan: Efficient implementation of leave-one-out cross-validation and WAIC for evaluating fitted Bayesian models.
We (that is, Aki) now recommend LOO rather than WAIC, especially now that we have an R function to quickly compute LOO using Pareto smoothed importance sampling. In either case, a key contribution of our paper is to show how LOO/WAIC can be computed in the regular workflow of model fitting.
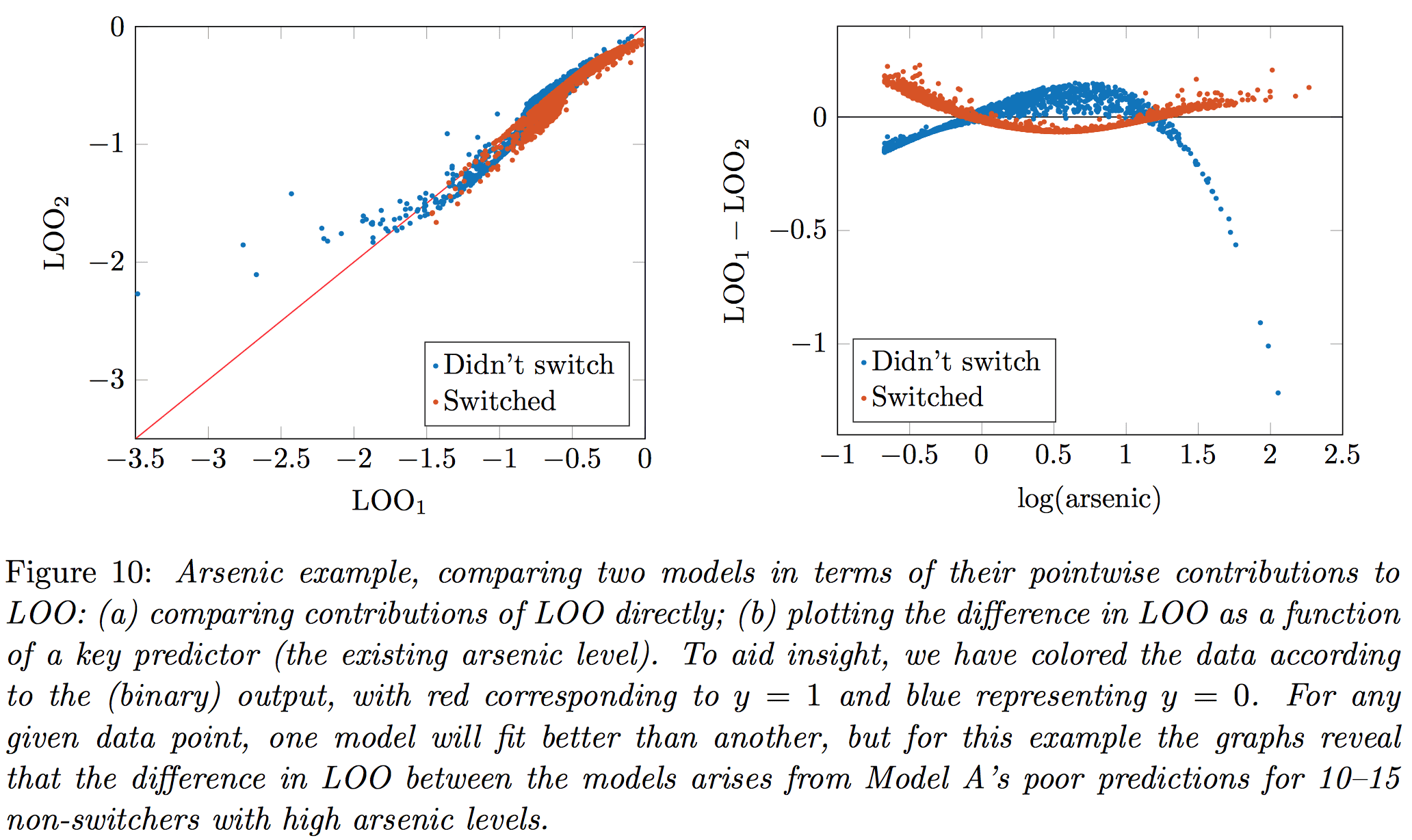
We also compute the standard error of the difference between LOO (or WAIC) when comparing two models, and we demonstrate with the famous arsenic well-switching example.
Also 2 new tutorial articles on Stan will be appearing:
in JEBS: Stan: A probabilistic programming language for Bayesian inference and optimization.
in JSS: Stan: A probabilistic programming language
The two articles have very similar titles but surprisingly little overlap. I guess it’s the difference between what Bob thinks is important to say, and what I think is important to say.
Enjoy!
P.S. Jonah writes:
For anyone interested in the the R package “loo” mentioned in the paper, please install from GitHub and not CRAN. There is a version on CRAN but it needs to be updated so please for now use the version here:
To get it running, you must first install the “devtools” package in R, then you can just install and load “loo” via:
library("devtools") install_github("jgabry/loo") library("loo")
Jonah will post an update when the new version is also on CRAN.
P.P.S. This P.P.S. is by Jonah. The latest version of the loo R package (0.1.2) is now up on CRAN and should be installable for most people by running
install.packages("loo")
although depending on various things (your operating system, R version, CRAN mirror, what you ate for breakfast, etc.) you might need
install.packages("loo", type = "source")
to get the new version. For bug reports, installation trouble, suggestions, etc., please use our GitHub issues page. The Stan users google group is also a fine place to ask questions about using the package with your models.
Finally, while we do recommend Stan of course, the R package isn’t only for Stan models. If you can compute a pointwise log-likelihood matrix then you can use the package.
The papers aren’t THAT different, since both links point to yours…
Fixed; thanks.
JSS link is wrong.
For anyone interested in the the loo R package mentioned in the paper, please install from GitHub and not CRAN. There is a version on CRAN but it needs to be updated so please for now use the version here:
https://github.com/jgabry/loo
Installation instructions are in the readme. I’ll post an update when the new version is also on CRAN.
Link to JSS and JEBS articles are identical. Can you fix?
Links are fixed; you just have to refresh the page.
I think there’s a typo on page 20 of the paper. The third line of the Stan model says
int y_1[N]
I imagine it should be
int y_1[N_1]
Also, in the generated quantities block:
vector[N] log_lik_2
should be
vector[N_2] log_lik_2
Hey, thanks! Dammit, that’s what I get for not using a workflow environment such as knitr.
Or org-mode (http://orgmode.org/worg/org-contrib/babel/index.html). :-)
The final two links both seem to point to the same tutorial.
This is making me scream . . . . Just refresh the page!!
Poor Andrew. You post three papers about the free software you are making and all you get are comments correcting your typos. So, just to balance things out: Thank you Andrew and collaborators for giving us Stan.
LOO/WAIC paper is now also in arXiv http://arxiv.org/abs/1507.04544, so that you can use that reference while waiting the paper to be accepted by a journal (arXiv version still has the typos in the code pointed out by Sean Raleigh).
And the Pareto smoothed importance sampling (aka Very Good Importance Sampling) paper, referred in the LOO/WAIC paper, has been in arXiv http://arxiv.org/abs/1507.02646 for a few days.
RE: CRAN, the latest version is now available (mostly). See the P.P.S. above.
Hi Andrew and Aki,
Great article and thank you for making a package the “LOO” package to calculate these information criterion for R.
Two questions:
1) The article doesn’t mention whether the WAIC/LOO/PSIS-LOO can be used to compare models of a time-series. From the Gelman et al. 2014, it seems that LOO-CV can be used to compare models in a time-series, as you assumed that each data-point is independent.. …is PSIS-LOO better than LOO-CV for time-series?
2) In the schools example which compares pooled, unpooled and hieararchical models, are you using different data (i.e. ggregated or averaged vs. individuals) on different models? How can you make inference on whether one model fits better than another?
See the updated version at Statistics and Computing http://link.springer.com/article/10.1007/s11222-016-9696-4 or arXiv https://arxiv.org/abs/1507.04544
1) WAIC/LOO/PSIS-LOO can be used to compare models of a time-series if the accuracy of predictions p(y_t|y_{1,..,t-1,t+1,…,T}) is interesting. Often in case of time series it is assumed that the observations after t are not available for predictions and LOO would be optimistic estimate of the accuracy of predictions p(y_t|y_{1,..,t-1}). This is easy to handle with time series specific cross-validation. PSIS-LOO is an approximation for LOO-CV.
2) See Section 5.
Thanks Aki. The appendices are really helpful. I asked these questions because I think PSIS-LOO would be handy for retrospective analyses for model comparison among state-space models for fisheries stock assessment.
I asked whether different data could be used to compare different model structure in the school examples because of the following passage:
“For example, the 8 schools data are available only at the school
level and so it seems natural to treat the school-level estimates
as data. But if the original data had been available, we would
surely have defined the likelihood based on the individual
students’ test scores.”
Do you mean to say, if you had student-level estimates you would use this technique to compare among the models at the school level to those that include a student-level? Wouldn’t this be different data and comparing to different models?
I ask because I wonder whether I could state-space models in fisheries stock assessment that had age-aggregate observations (catch-per-unit effort) to models that had age-structured level observations (catch-at-age per unit effort). Similar to your statement above.