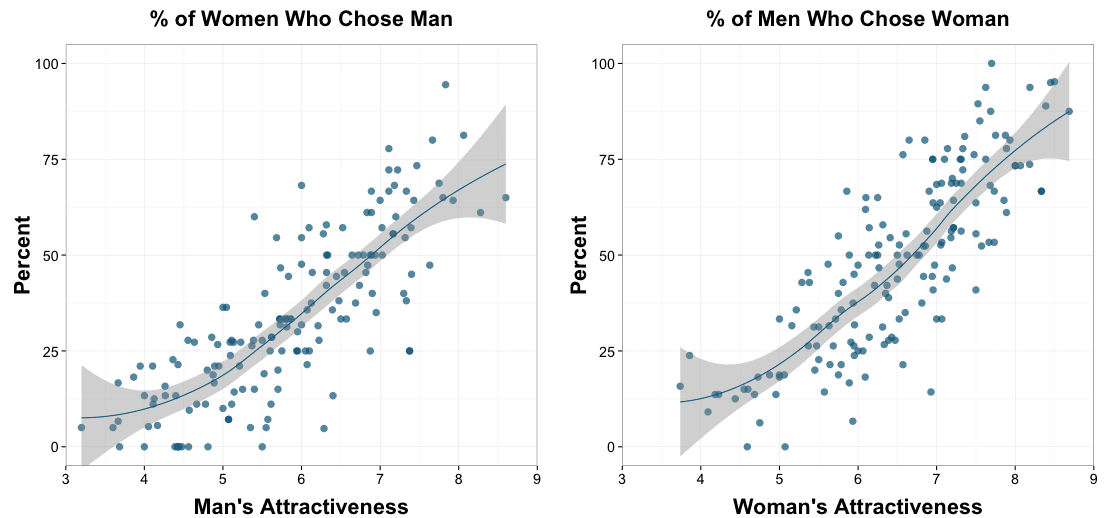
Jonah Sinick posted a few things on the famous speed-dating dataset and writes:
The main element that I seem to have been missing is principal component analysis of the different rating types.
The basic situation is that the first PC is something that people are roughly equally responsive to, while people vary a lot with respect to responsiveness to the second PC, and the remaining PCs don’t play much of a role at all, so that you can just allow the coefficient of the second PC to vary.
Despite feeling like I understand the qualitative phenomenon, if I do a train/test split, the multilevel model doesn’t yield better log loss, (though there are other respects in which the multilevel model yields clear improvements) and I haven’t isolated the reason. I don’t think that there’s a quick fix – I’ve run into ~5 apparently deep statistical problems in the course of thinking about this. The situation is further complicated by the fact that in this context the issues are intertwined.
And he adds:
Do you know of researchers who work at the intersection of collaborative filtering and hierarchical modeling? Googling yields some papers that seem like they might fall into this category, but in each case it would take me a while to parse what the authors are doing.
I am surprised nobody has answered this query….
If you consider PCA similar to factor analysis and note that matrix factorization is one of the most popular techniques in collaborative filtering then its clear that much of the literature (at least the probabilistic part) is at the interface of hierachichal models and collaborative filtering and involves PCA like models.
A lot of signal processing papers on blind source separation are just as relevant for collaborative filtering.
A place to start is here:
http://www.cs.toronto.edu/~rsalakhu/papers/bpmf.pdf
http://www.hindawi.com/journals/cin/2009/785152/
http://papers.nips.cc/paper/4572-random-function-priors-for-exchangeable-arrays-with-applications-to-graphs-and-relational-data.pdf
http://www.hiit.fi/u/dikmen/nips11/
https://www.cs.princeton.edu/~blei/papers/BleiNgJordan2003.pdf
Also the theory behind the Aldous-Hoover represenation is very interesting!