Aki Vehtari, Pasi Jylänki, Christian Robert, Nicolas Chopin, John Cunningham, and I write:
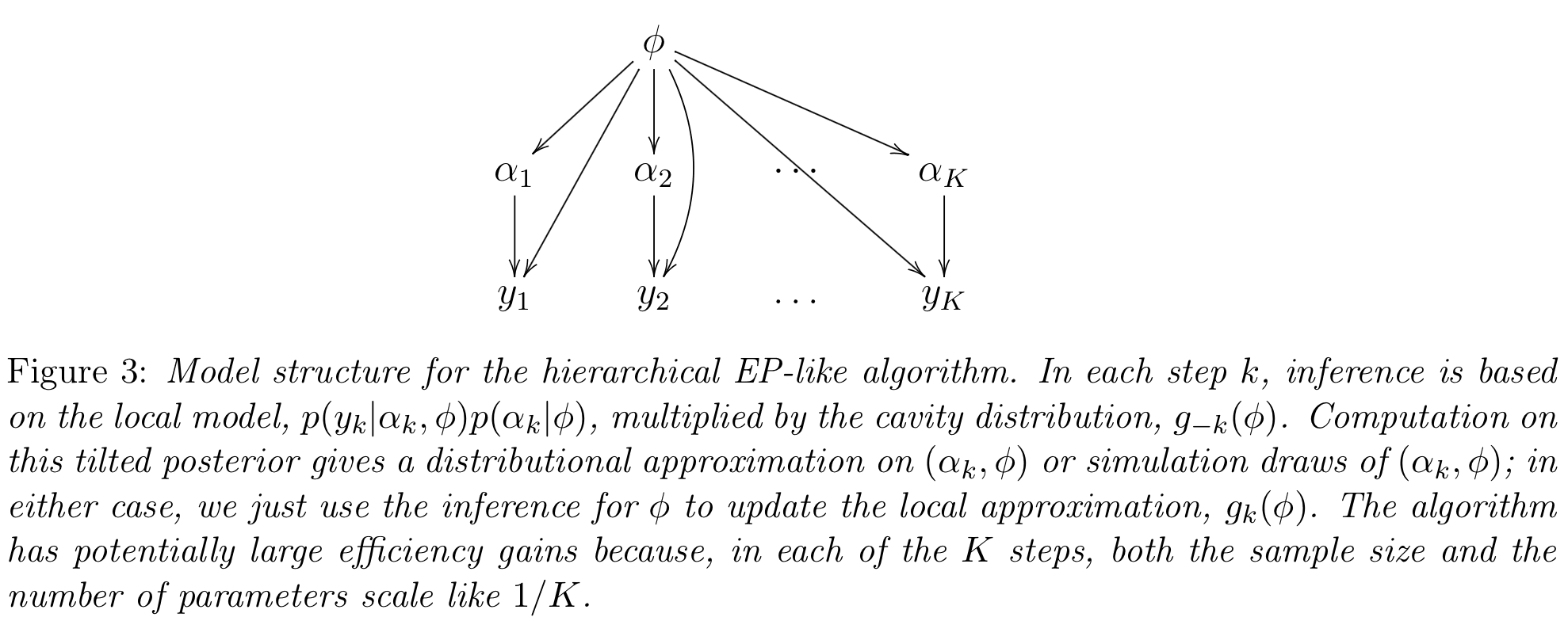
We revisit expectation propagation (EP) as a prototype for scalable algorithms that partition big datasets into many parts and analyze each part in parallel to perform inference of shared parameters. The algorithm should be particularly efficient for hierarchical models, for which the EP algorithm works on the shared parameters (hyperparameters) of the model.
The central idea of EP is to work at each step with a “tilted distribution” that combines the likelihood for a part of the data with the “cavity distribution,” which is the approximate model for the prior and all other parts of the data. EP iteratively approximates the moments of the tilted distributions and incorporates those approximations into a global posterior approximation. As such, EP can be used to divide the computation for large models into manageable sizes. The computation for each partition can be made parallel with occasional exchanging of information between processes through the global posterior approximation. Moments of multivariate tilted distributions can be approximated in various ways, including, MCMC, Laplace approximations, and importance sampling.
I love love love love love this. The idea is to forget about the usual derivation of EP (the Kullback-Leibler discrepancy, etc.) and to instead start at the other end, with Bayesian data-splitting algorithms, with the idea of taking a big problem and dividing it into K little pieces, performing inference on each of the K pieces, and then putting them together to get an approximate posterior inference.
The difficulty with such algorithms, as usually constructed, is that each of the K pieces has only partial information; as a result, for any of these pieces, you’re wasting a lot of computation in places that are contradicted by the other K-1 pieces.
This sketch (with K=5) shows the story:

We’d like to do our computation in the region of overlap.
And that’s how the EP-like algorithm works! When performing the inference for each piece, we use, as a prior, the cavity distribution based on the approximation to the other K-1 pieces.
Here’s a quick picture of how the cavity distribution works. This picture shows how the EP-like approximation is not the same as simply approximating each likelihood separately. The cavity distribution serves to focus the approximation in the zone of inference of parameter space:
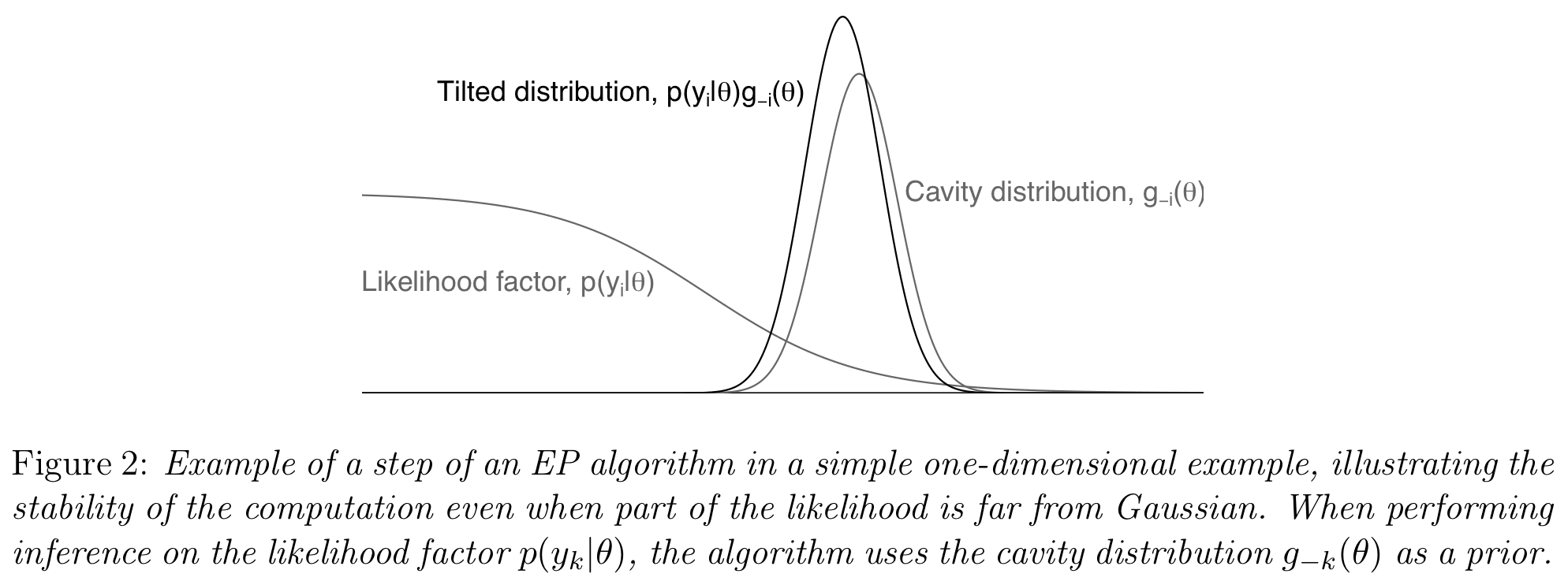
But the real killer app of this approach is hierarchical models, because then we’re partitioning the parameters at the same time as we’re partitioning the data, so we get real savings in complexity and computation time:
EP. It’s a way of life. And a new way of thinking about data-partitioning algorithms.
Is there not a tradeoff between efficiency and bias?
Will you be resampling the partitions? Or do you only partition once?
For example, with reference to the first “flower power” graph above. Consider the case where the area of overlap is very small. Suppose also it is highly variable across different samples of partitions (e.g. across a bouquet of “flower power” graphs). Then the estimator is consistent, but it might be ways off in any particular sample. The reason, I think, has to do with artificial clustering of the data.
Just shooting from the hip here.
Fernando:
We were not planning to resample the partitions but it’s an interesting idea, maybe worth thinking about. Thanks.
Neat!
Hi Andrew,
Glad that you find this interesting, as we do too! In fact we have a paper at NIPS that is quite close in spirit, that I hope you will find of interest:
http://papers.nips.cc/paper/5596-distributed-bayesian-posterior-sampling-via-moment-sharing
We were going to look into hierarchical models next :)
cheers,
-yw
Yw:
Cool. I guess the time was ripe for this idea. It’s a good thing we’re not all working together, or we’d have a paper with 11 authors!
Seriously, this does seem to be to be the way to go for data-splitting algorithms, and it’s good to see a similar algorithm presented using different notation. When I worked on this problem with Zaying Huang, back in 2005, I didn’t know about EP, and all we could think of was to do the inferences completely separately. But then you don’t big speed improvements, which is why we didn’t even bother submitting that paper to a journal. With EP, and also with Stan, we have so many ways to go here that I’m thinking this might end up being the way to fit big models on big datasets.
Yap, I’m very excited too. Looking forward to reading your paper in detail, looks like you’ve gone in much more depth than we had. cheers.
Andrew: Does your approach also work for priors of the regression coefficients that impose strong dependency structures? For example Gaussian Markov random field priors for latent temporal or spatial effects as they are usually used within the INLA approach.
One of the first successful applications of EP is to Gaussian processes, which is closely related:
http://www.jmlr.org/papers/volume6/kuss05a/kuss05a.pdf
You cite the Scott, et al working paper on Consensus MCMC. There, they are sampling at the publisher or URL level and assuming (for now, at the time of pub) the URLs are iid. Then there’s Cleveland’s Oct 2013 work on Divide & Recombine (D&R), not to mention that much of this data splitting research stream seems to follow from Breiman’s random forests approach. Given the fact that there doesn’t seem to be too much concern with dependence structures (overt, hidden or otherwise) in the previous literature and following up on Paul’s query re “dependency structures,” how does your data splitting alg partition the data without destroying variance?
I think this is a nifty idea, but I’m not sure the paper actually convinces me that it will work (Later note: the comments below don’t really end up reflecting that I like the paper. I like the paper, but I think it has problems):
– Complexity calculations are one thing, but it’s hard to make the case that this is a scalable algorithm without demonstrating it. I’d love to see some weak scaling plots (I don’t think it will be strongly scalable, but it may be weakly).
– The example (simulated logistic regression) is really boring and doesn’t really live up to the claimed flexibility. If the astronomy example was real (with data and pictures and results), then it’s probably interesting enough, but without that it’s hard to actually see if this would work for a realistically complicated problem. (The logistic regression case would be great, however, for demonstrating scalability!)
– If I read this correctly, this idea basically requires log-normal priors on variance-ish parameters. I can’t reconcile this (without doing some pen and paper work) with your work on weakly informative priors. A log-normal on the standard deviation is probably not a great prior!
– This also doesn’t massively match with the INLA experience. Consider the “latent gaussian model” parameterisation \theta = (x , \phi), where \phi has the same meaning (it’s the variance parameters etc), x has a normal prior, \phi has an appropriate prior. Then x | y, \phi is pretty much normal, so the EP approximation will work great. But the posterior marginal for \phi is probably going to be very non-Gaussian, so I don’t see how EP is going to capture this well. This would probably be fixed by using different approximating families in the hierarchical model for g(x) and g(\phi), with the latter being more flexible.
– This one is probably a reflection of my ignorance around the EP literature, but is it obvious that your algorithm converges?
– A big data thing: I don’t think you can capture sparsity with the assumed posterior structure. You need posterior dependence between the coefficients (or equivalently the weights), which I don’t think the EP structure will capture. That being said, I may be very wrong about that and I assume that at least one of the authors will tell me that :p
What’s wrong with lognormal on a standard deviation / variance? I have some brightness measuring device that measures on a scale 0-1, and for the stuff I’m pointing it at it is going to show 0.17 +- something, and something is about 0.1 but could be in the range 0.05 to 0.2 without much surprising me… so stddev ~ lognormal(log(0.1),log(2)/2) that kind of thing? Perhaps this is more realistic in measurement instrument models?
In general, the problem is that it puts, a priori, no mass on the component not being there. Which is problematic, because if you’re not careful, you shrink your estimate towards a non-zero part of the parameter space and basically force extra complexity. For one parameter this is probably not terrible, but for many it’s a bit of a disaster. Andrew wrote a couple of really good papers about this, and I wrote a (long) one that I, at least, am quite fond of (http://arxiv.org/abs/1403.4630). At the very least it has the reference to the appropriate Gelman et al papers.
However, as always with prior choice, if you have elicited your log-normal using expert information (as you have above) and you’re prepared to stand by it, then that is the best prior for your problem.
Bayesian inference is interpreted in light of the model choice, and hence in light of the prior selection. Crap in, crap out :p
Is there a variance parameter in any sensible model anywhere which should have positive mass on variance == 0 ??
Does anyone use variance priors that actually have point masses on 0 in any real-world applications of fully Bayesian inference?
They do sometimes, but what I meant to say was positive density at zero. Which means that the mass in small sets containing zero doesn’t shrink too fast.
Yes. When doing full Bayes we want priors p(sigma) that don’t go to 0 at sigma=0. But when doing marginal penalized maximum likelihood estimation, we do want p(sigma) to go to 0 at sigma=0 in a linear way. We discuss this a bit in BDA and also in our recent papers with Yeojin Chung et al.
Ooh! I haven’t read that one!
Scanning it quickly, that sort of degenerate maximum likelihood case (where the gradient doesn’t vanish at the true boundary value) was covered recently by Bochkina and Green (http://projecteuclid.org/euclid.aos/1410440627) who showed that if you have a prior like p(sigma) = O(sigma^{-alpha}) for alpha<1, near sigma=0, then the Bayes estimator is super-efficient. I wonder if that carries over to teh penalised likelihood case?
Dan: You have good comments (as always). I agree the paper has problems (No paper is perfect…)
– Scalability: Our goal is to get this into Stan. Stan needs some modifications before any timing tests would be representative of what is possible. Scalability will depend very much on the model structure.
– Example: Yes the example is boring. We are working on more examples. We are working with the astronomers who are working on with the real data. The astronomy problem has much more complexity than mentioned in the paper and it will be interesting test for scalability in data size, the number of parameters in different levels, and complexity of model structure.
– Priors: Priors do not need to be log-normal. In a same way as a non-normal likelihood contribution is approximated with a normal distribution, the prior contribution can be approximated with a normal distribution (preferably in non-restricted transformed parameter space)
– INLA experience: EP approximation is required only for global parameters, to keep it scalable we will likely have much less global parameters than data, and thus I would think that the posterior for those parameters will be well approximated by Gaussian (in non-restricted transformed space). With small data we would not use this algorithm. With certain model structures we might have a large number of parameters in EP approximation and then we might have the problem you mentioned.
– Convergence: there is no proof of convergence for EP
– A big data thing: I’m not sure if understood this comment, but I’m happy to discuss more.
– I cannot tell you how excited I am about a black box that would do this sort of thing! One of my new years things will be to work out how to add (simple) models / priors to STAN so I can have a proper play
– Yes! That problem looked really cool, which may have influenced my feelings about simulated logistic regression…
– I’m slightly uncomfortable about approximating priors in cases where the model is complicated enough that you need the prior to regularise the inference. It’s not clear to me that a prior that regularises these problems has a Gaussian approximation that does as good a job. If these are nuisance parameters, this is probably an academic point, but if one of these parameters is an object of interest in the inference, I would want to keep my careful (subjective/weakly-informative/structurally aware) prior. But the problems where I’ve hit this sort of feature haven’t really necessitated this level of parallelism, so it may be a completely irrelevant gripe…
– There was also that Omerond paper from a few years ago that used skew normal (or maybe skew t) VB, that seemed to work quite well for a small number of parameters, which may be a flexible enough family to consider here, practically. Scanning through the paper again, I don’t think I fully understood the hierarchical section, so I still think that modifying the family for different levels of the hierarchy may have good (low cost?) benefits, I absolutely love the conditional specification of the joint distribution.
Dan:
If you think the shape of the likelihood in classification it doesn’t resemble Gaussian at all. However replacing the likelihood with Gaussian is different than approximating the likelihood contribution given other data with Gaussian. The latter works quite well. Additionally we can examine the tilted distribution for the prior, which is non-Gaussian. Of course it’s still possible that the joint approximation is bad etc.
Dan:
Thanks for the comments.
Regarding whether the algorithm “works,” I think it already works in the sense that people already doing data splitting, approximation, and combination for Bayesian inference, and this is a more general approach. To put it another way, I think you’re comparing our method to a desirable, but nonexisting algorithm that does all sorts of great things. But we’re viewing it as a way to do Bayesian data splitting more sensibly, effectively, and efficiency.
Regarding the examples: as we said in the paper, “We have not yet performed runtime comparisons because our implementation has many places where we can increase its speed. . . . We plan to do more systematic scalability testing once we have increased the efficiency of some of our computational steps.” Similarly for the examples: you may find hierarchical logistic regression to be boring, but as a social scientist I find hierarchical logistic regression to be extremely important, and it’s a problem I want to be able to solve. The astronomy example is interesting and we are planning to do more, but we thought the idea was so great we wanted to get our paper out there right away.
I’d rather share our idea with the world as soon as it’s in presentable form, than keep it hidden away until we can prove how great it is. Research proceeds in fits and starts, and it may well be that someone who reads the paper we’ve posted will be able to make progress by coming up with improvements that we never would’ve thought of. So we are currently working on implementing this idea in a more black-box way and applying it on other problems, also on making the computations more efficient so we can do meaningful speed comparisons. But no point in making everyone wait until we’ve done all this!
On some of your other points: Yes, our approach will work with weakly informative priors. For simplicity we presented the algorithm with flat priors but that would not be necessary. Regarding the problem of p(phi|y) being far from the approximate family: yes, this in an issue. But in practice when fitting big hierarchical models, it is typically the least of our worries. Consider that, in many applied settings, users are happy with marginal maximum likelihood, that is, a point estimate of phi. Sure, I don’t want to miss out on any of the posterior uncertainty in phi, but this is not my largest concern.
No, it’s not obvious that our algorithm converges. It’s a stochastic approximation algorithm and much depends on how much simulation is done at each step. I expect that stability will be a key concern in developing the black-box version of this algorithm for Stan.
Finally: to the extent that the model has complex dependence between the local parameters, there will not be such great computational benefits from partitioning the data. In our examples, the local parameters are independent given the shared parameters, and the number of shared parameters is relatively small, which is a best-case scenario for our method (and, for that matter, with any data-splitting algorithm). If you have lots of dependence, you can still do data splitting and it still could have computational advantages, but you wouldn’t get that extra benefits of the number of parameters in each batch scaling like 1/K.
Thanks for your response, Andrew!
Just to be clear, I don’t have a problem with logistic regression, it’s more the simulated data that makes it boring. New algorithms always tend to work on simulated data (*always…), whereas real data tends to ruin models/algorithms. A paper of this sort definitely needs a simulation study, but alone I don’t find it convincing.
I agree with you on the “timeliness vs completeness” trade-off. I’m probably just reacting to having been burnt before on promises of parallelism that never delivered (one memorable time “massively parallel” meant “we did it on an eight core laptop”). As you pointed out in the paper, not every “on paper” parallel method leads to something usefully scaleable. (Incidentally, “usefully scalable” was my internal definition of “works”. I don’t really care about exactness, I’m thrilled for hard problems like this if you can get one significant figure)
One final passing observation: My absolute favourite thing in Section 3.1 is that the EP approximation respects the hierarchical decomposition (it was always a problem for me that vanilla EP tended to treat all the parameters in one block rather than respecting the structure). When the alphas are jointly a priori Gaussian, it’s probably possible to exploit existing software / techniques for parallelising direct matrix factorisations to speed up the “step 4 and beyond” operations. This software would probably also be useful for load balancing / graph decomposition when it comes to making a practical implementation. To that end, perhaps the mean vectors M should be joined with the alphas in the implementation of the model in 3.2, as all that leads to is a massive Gaussian with some dense rows and most modern software libraries have ways of dealing with dense rows without ruining parallelism (basically, shunt them to the back).
Dan:
You’re a better man than I am. My new algorithmic ideas often don’t even work on simulated data! To put it another way, we wanted this idea out there right away, but I didn’t want to even put it on Arxiv until we had an implementation that, at least, worked on a simple fake-data problem! I don’t believe that the fake-data example gives convincing evidence that the algorithm will be useful in real problems; rather, I consider it a minimal step, in that I wouldn’t want to post the paper anywhere without it.
Andrew and colleagues – nice work, I’m also a big fan of EP.
You might also be interested in
http://papers.nips.cc/paper/3669-large-scale-nonparametric-bayesian-inference-data-parallelisation-in-the-indian-buffet-process.pdf where we combine message-passing with MCMC to do data-parallel inference. Essentially the data is split up across nodes which communicate via message passing ( which can be EP, BP, or variational message passing). This paper from 2009 predates many similar papers that have been published recently on data partitioning Bayesian inference. The ideas in it are quite general, although we apply it to a (particularly challenging) class of Bayesian model, based on the IBP.
Hi Andrew,
What you think about the problem of analyzing millions of temporal datapoints using posterior/prior updating in a Bayesian regression problem?