I happened to come across a post from 2011 about some work of Roland Fryer, a prominent economist who works in education research. In an article, Fryer made the offhand remark that “test scores have been largely constant over the past thirty years,” a claim that was completely contradicted by one of the graphs in his own paper:
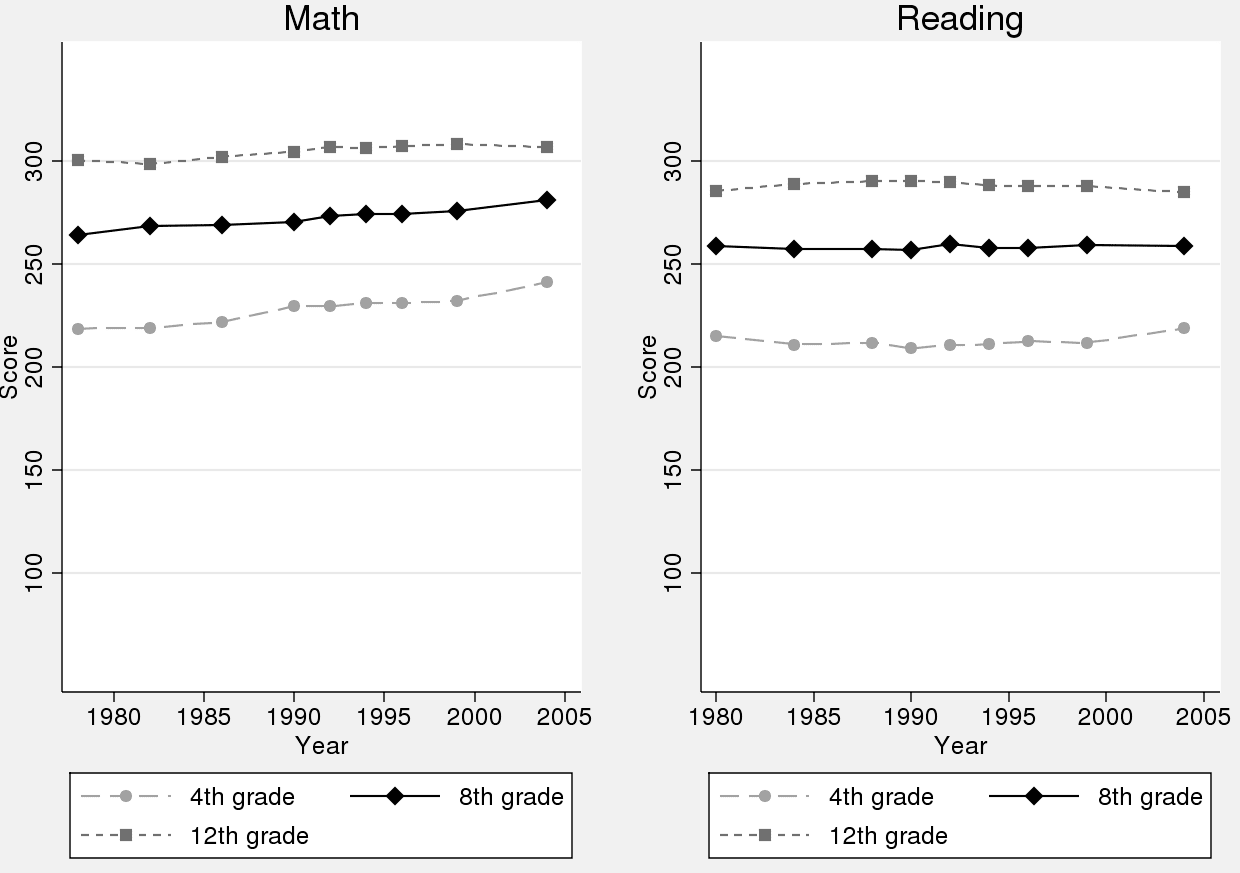
As I wrote in my earlier post:
Once you get around the confusingly-labeled lines and the mass of white space on the top and bottom of each graph, you see that math scores have improved a lot! Since 1978, fourth-grade math scores have gone up so much that they’re halfway to where eighth grade scores were in 1978. Eighth grade scores also have increased substantially, and twelfth-grade scores have gone up too (although not by as much). Nothing much has happened with reading scores, though.
It seems that the “schools are failing” storyline is so strong that no data can kill it!
P.S. I’ve not talked with Fryer in many years so I have no idea what was going on when he wrote this paper or, indeed, if there was just some oversight in the writing that led to the error, or if I’m misinterpreting the data in some way, or what happened to that paper since I posted on it, or what Fryer is dong now. My point here is not to slam Fryer but to just marvel on the power of the storyline. Kaiser Fung has talked about “story time” being what researchers do after they’ve completed the data analysis and are interpreting their results. But, in this case, “story time” seems to have come first.
P.P.S. I sent the above to education blogger and statistician Mark Palko, who wrote:
1. It’s possible that Fryer was focusing on 12th grade results. You could argue that gains in fourth and eighth grade don’t count for much unless they’re sustained. (then why include the earlier grades in the graph? Maybe because it’s badly designed.) There’s still an upward trend but not nearly as dramatic as that of the lower grades;
2. That said, if Fryer is talking about seniors, that focus may be misplaced. I recently contacted Diane Ravitch to see if she had run across concerns about basing policy on low-stakes tests. This was her reply:
“I am no expert on statistics but when I served on the NAGB board, I recall that we spent an entire meeting discussing the lack of motivation of seniors. They knew the tests were no stakes. They made random patterns of answers. We stopped testing 12th grade.”
NAGB oversees NAEP;
3. NAEP scores for the US or for New York City schools?;
4. If the graph is the whole US, I don’t see how it would tell us anything meaningful. In the more than quarter century shown there were enormous social, economic, demographic, educational and legal changes (for example, changing policies toward students with disabilities might explain part of the increased costs and smaller classes Fryer mentions). I don’t see how we can draw any inference about things like per student spending.from these graphs.
Bob Somerby at the Daily Howler writes often about how not disaggregating NAEP scores masks student achievement. For example, here are national NAEP scores for the long-term math trends, for age 13, from 1978 to 2012, disaggregated by student race:
White: 272 to 293 [+21 points]
Black: 230 to 264 [+34 points]
Hispanic: 238 to 271 [+33 points]
Other: 273 to 305 [+32 points]
However, the overall change for NAEP long-term math trends, age 13, from 1978 to 2012, was: 264 to 285 [+21 points].
The achievement gap in math is shrinking while at the same time scores across all groups are going up. Definitely a good thing, assuming the NAEP is a reasonable estimator of student understanding.
So while we “marvel on the power of the storyline,” I think it is reasonable to ask why this particular story is so resilient even in the face of data. I have my own thoughts, but would prefer to hear the thoughts of those who study education and education policy on why this is the case.
One explanation that I have read is that it is easier to sell educational reform if the perception is that scores are stagnant or falling.
+1, LJ Zigerell
But then, where does the unshakable commitment to educational “reform” come from?
Is it interests? Do the club of rich reform backers and the politicians they favor stay on this path because there is some reformed model of education that better suits the needs of employers today? That would not necessarily change if test scores rose – it might be that they see an educational system devoted to raising test scores as desirable not simply for producing literacy and numeracy, but because the skills and habits of mind such an educational regime engenders meet employers’ needs in an economy polarized between a top layer of knowledge work and a large bottom layer of low-wage services.
Or is it a delusional commitment to the theory that human capital determines earnings? If education determines marginal productivity and marginal productivity determines earnings – that is, if a host of factors relating to institutions and market structure can be ignored – then the growth and persistence of the inequality, post-1980, must imply a deficient educational system. For many economists, this is indeed the default model of income distribution. If you were a tycoon who (1) had a social conscience and (2) owed everything to the market structures and institutions of the post-1980 world (e.g., Bill Gates, Michael Bloomberg…), then it could be comforting to accept such human capital fundamentalism and “give back” by sponsoring educational reform, whatever the statistics say.
I think pure motives for educational reform include a concern for raising achievement and reducing achievement gaps and a belief that more competition will improve education because such competition produces an incentive for teachers and administrators to provide a better education.
Concern for raising achievement is reflected in the push for higher standards; concern for reducing achievement gaps is reflected in grading school districts on student achievement in groups disaggregated by sex, race, and socioeconomic status; and belief in competition is reflected in charter schools and grading the performance of individual teachers.
There are probably a lot of other motives that I missed, especially given that reform is filtered down through superintendents, principals, and teachers, who might have their own interests. It’s also worth noting that some reforms might work at cross purposes with other reforms.
What you describe may well be the proximate motives for reform; they may feel pure, but I think it’s worth interrogating the beliefs on which they are built. In addition to beliefs about the efficacy of competition, the focus on education [education education] often stands on a belief that today’s social crisis *is* a crisis of education and skill [skills for the 21st century, skills for the knowledge economy, skills for global competition], not of the demand side of the labor market and of [absent] opportunities for social mobility.
Where does that belief come from? If you want to believe that poverty is not the result of an economic restructuring that has sucked all the gains to the top and cut off many ladders of opportunity, then perhaps it helps to believe that the problem lies in the schools. Labor market outcomes then get treated as direct evidence that schools are failing, which encourages mindless perpetual reform, teacher-bashing, and dire international comparisons, even in the face of evidence of improved educational performance and reduced achievement gaps. Hence, even in Fryer’s paper (which is a demolition of the teacher incentives often used in these reforms) – the picture of continuing educational crisis gets a free pass.
I’m not sure that it’s a good idea to drill down any further than the ideas themselves. I think that there’s a danger that focusing on beliefs and motives underlying an idea can lead to dismissal of the idea only because of the presumed underlying belief or motive.
Well even with Hispanic scores going up so much, their growth in terms of proportion of the population over that timeframe is going to dampen the combined effect size.
An example where better labeling would make things so much clearer. Why does the graph start at what might be 50 with a bunch of empty space above it? Why doesn’t it include 210, 220, etc. or even 205, 210, 215, etc.?
I’m reminded of the film of the lava flow in Hawaii. Looks freaking awesome in the news reports. Then look at the aerial photo and you see a narrow strip of lava, just a little stream of it in a huge landscape.
Jonathan:
My guess about the “why” question is that that the author of the paper did not really care about the graph, and that he had a student make the graphs and gave the student little direction or feedback.
So I’d push the question back and ask: Why is that graphs were not considered a serious part of this project? I think the idea is that the graph is just about presentation, not about research. But, as this discussion has revealed, a bad graph can actually obscure a strong pattern in the data.
So I think it was a mistake in this case for the author of the paper to not put some time into the graphical display (in addition to the problem with the white space, also there’s a problem with the labeling of the lines on the graph). Just like it was a mistake for Reinhart and Rogoff to apparently think of data processing as a sort of menial labor that wasn’t worth their serious attention, hence the notorious Excel error that people are still talking about.
Also, dropout rates probably factor in as well. Someone who scores sub-200 in 4th Grade Math may not make it to the 12th. So as there is improvement in the lower grades, this composition effect drags down average scores in the higher ones.
A worthwhile factor to consider in addition. Should probably control for dropout rate as well as an additional variable. Has the dropout rate in lower grades been increasing over the lifetime of the study? I don’t know.
“America spends more on education than it has ever before: per-pupil spending has increased (in 2005 dollars) from approximately $4,700 per student in 1970 to over $10,000 (Snyder and Dillow, 2010). Yet, despite these reforms to increase achievement, Figure 1 demonstrates that test scores have been largely constant over the past thirty years.”
http://www.nber.org/papers/w16850.pdf
Then why don’t you plot spending vs achievement subset by year/location? Also that graph seems to depict some kind of average… if so where did the error bars go? Am I crazy or are these things common sense?
Is that in real terms? (Allowing for inflation $4,700 to $10,000 in 40 years is probably a substantial drop. I can’t find the actual figures, but the same source gives 4.6% of GDP on education in 1970 and 4.6% of GDP in 2009. That would suggest that spending has risen in real terms but not ahead of GDP (so presumably not keeping up with wage inflation etc.). There was also a big dip in expenditure between 1970 and 2009 In terms of GDP.
I don’t know. But no including error bars and no plotting the two phenomena of interest against each other… if the reason is too much complication due to inflation/etc then why bother mentioning it?
It’s real, not nominal dollars, indexed on 2005: “spending has increased (in 2005 dollars)”
Why would he use error bars? Isn’t he reporting on the population mean score of a standardized test, not a sample mean? Or is this an estimation of how the entire population _would_ test based on the sample tested? I always thought testing numbers like these simply reported on those tested.
Question:
You ask, “why don’t you plot . . .”. Just to be clear, I’m not plotting anything. All I did was copy and paste a graph from Fryer’s paper, to point out that his own evidence appears to contradict what he is saying about test scores remaining constant. A lot more could be done to analyze trends in test scores but the point here is that he seems to be taking for granted the standard schools-are-failing narrative even though this narrative is contradicted by his own graph.
Bad wording on my part. I thought it was clear I was referring to the paper, not here, when I linked to it. Sorry about that.
Are we really giving the same test in 2005 as 1980? When I see that trend, I don’t think “gee we’ve made a lot of progress” I think “there is a really flat line with a slight upward tilt”. When I consider that it covers 30 years of testing, and I think about how many times we’ve changed the SAT and the school assessment tests and things… and then there are no units on these graphs, it’s hard to know what +10 “points” means qualitatively for a person’s life… what is *practically significant* change? It’s not hard to see where Fryer is coming from… he’s not impressed. perhaps he should be, but maybe not. I think you’d have to break things down more carefully and try to come up with consequences for this amount of improvement and try to put a scale on *practically significant differences* before you can say either way whether we’ve been “flat” or “improved a lot”.
The rule of thumb that I have seen in education circles is that 10 points on the NAEP is roughly one grade level. So, by that metric, a 20-to-30-point increase is substantively important.
Apologies if this is a silly question but are 4th, 8th and 12th graders all taking the same test?
No
If this is true, then I see little reason for these graphs to not be normalized to the 1978 values. Maybe even set the scale so that the first data-points are at zero, so the y-axis reads “percent change from 1978 score.” As the reading scores are effectively flat and math scores improve 8-12%, one has no excuse to have so much whitespace in the figures. Well maybe the math and reading y-scales ought to be the same, to highlight difference in performance improvement, which out to prompt the question: “Why did this happen?”
Right, and comparisons *between* grades at the same time point are completely useless. You might argue that comparing the 1980 grade 4 to the 1984 grade 8 would have some merit, but with testing methodology also changing… it’s not a straightforward comparison.
“Students participating in the assessment responded to questions in three 15-minute sections. Each section contained approximately 21 to 37 questions. The majority of questions students answered were presented in a multiple-choice format. Some questions were administered at more than one age. ”
The top score is 500. The report doesn’t say a minimum score but but the lowest skill level it describes for 9 year olds is 106.
http://nces.ed.gov/nationsreportcard/subject/publications/main2012/pdf/2013456.pdf
Math stuff starts around page 30.
I do think that regardless of the paper Andrew posted about, the NAEP people have thought carefully about the measurement issues.
THere are some better graphs on this page if you don’t want to look at the whole report. http://nces.ed.gov/nationsreportcard/pubs/main2012/2013456.aspx
And this also describes the “levels” for each of the three grades.
http://nces.ed.gov/nationsreportcard/mathematics/achieveall.aspx
As I understand it, they set grade level standards (they are in that big pdf) and then on the basis of the scores students are put into the basic, proficient and advanced levels for their age groups. I assume that the idea of the multiyear comparisons is to compare within grade but you can also look at the percent who are at least proficient at each grade level.
One thing to keep in mind is that NAEP sample sizes in the distant past were much, much smaller than today’s sample sizes. For the couple of decades of very strong sample sizes, we see grinding 3 yards and a cloud of dust progress in Math: that’s both plausible and heartening. In Reading, we don’t see much progress over the last 20 years, but considering the demographic changes going on, stability has to count at least as a small victory.
While I figure the lowest possible score is 0, what is the highest possible score on these tests? Are perfect scores for the different grades the same value in the units on these plots? Maybe these tidbits of information are buried somewhere in the paper and I just missed them, but I think they ought to be on these plots.
Test scores have been going up since the Jeff Spicoli Era of the 1970s, especially if you adjust for the demographic shift among students toward lower scoring ethnic groups.
Scores are going up if you adjust for low scores?
That is what he’s saying, but it doesn’t have to be nonsensical. If we are trying to get to the treatment effect of the educational system, and the demographic is flooded with out-group immigrants who have a lower base starting point, we wouldn’t want to infer a lower (or slower growth) of scores is due to poor education, but due to shifting demographics.
I don’t know if that’s true, but it does provide a reasonable basis for adjusting for some demographic shifts.
You can see it in the report and the first comment here. There has been real improvement among Hispanics but it started from a lower base and since the proportion of the sample that is Hispanic has more than doubled you need to consider that.
What is the full margin of error in these NAEP numbers ?
What exactly are they attempting to measure ?
GIGO
http://nces.ed.gov/nationsreportcard/subject/publications/main2012/pdf/2013456.pdf
Technical notes start on page 52.
It says you can get the standard errors here.
http://nces.ed.gov/nationsreportcard/lttdata/
Interesting
http://nces.ed.gov/nationsreportcard/tdw/analysis/infer_guidelines.aspx
Pingback: A week of links | EVOLVING ECONOMICS