Is it really “often easier to win a rematch than to defend a championship”?
The quoted bit above comes from Tyler Cowen, writing about the Anand/Carlsen world championship rematch. I’m still not used to the idea of a new world championship match every year but I guess why not?
Anyway, here’s my question. Tyler Cowen knows a lot more about chess than I do, so I’m inclined to take his word on these things, but . . . really? Is it really often easier to win a rematch than to defend a championship? My impression is that chess rematches are generally won by the victor of the first match. Consider Karpov-Korchnoi and Kasparov-Karpov (not counting that first match that never came to an end). But I’m no expert on chess history, and I imagine there could be lots of data at lower levels (for example, national championship matches)?
So does anyone know? My intuition would be that, statistically, it would be unlikely for the former champion who lost the first match to then win the rematch, but maybe not? Or maybe I’m missing Cowen’s point?
Chess piece survival rates: some graphical possibilities here
Another Tyler Cowen link led me to this graph of chess piece survival rates, posted by Enrique Guerra-Pujol:
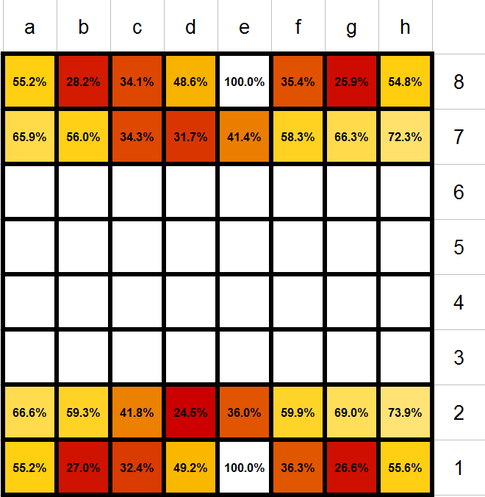
This is great. But now let me complain a bit about the display:
1. The lines are too thick. They’re so thick that this is about all I notice. They’re as thick as the black frames of hipster glasses. Bad news. The display just doesn’t look like a chessboard.
2. “48.6%”? Huh? This is the sort of hyper-precision we don’t like here. It’s hard to see what’s going on with that sort of detail.
3. Kings do get captured—that’s just checkmate, right? So this could be shown too.
OK, the graph can be better. But here’s what I really want to see:
Now that we have the idea of a spatial display for summarizing chess games, I’d like to see where the pieces get captured. I’m not sure the best way of doing this but perhaps a separate mini-chessboards for each piece, with a heat map showing where the piece gets captured? The maps for the pawns could be combined in some clever way, as they will mostly be captured in their own files, I assume.
P.S. Also it would be fun to see survival times: not just if the piece was captured, but when it was captured. Come to think of it, it would easy (given the data) to plot survival curves for each of the pieces, most simply with 16 graphs showing, for each piece, the curve for Black and the curve for White.
Perhaps the comment was motivated by the exploits of Botwinnik, who won rematches against Smyslov and Tal…
I’m not sure of the hyper-precision complaint. This data was probably aggregated from so many games that the decimal might be something we could trust?
Rahul:
The point is that the percentages will vary, for example by era or by skill level of the players, so it’s essentially meaningless to get an extremely precise average over the games in some particular database.
I agree. But also, even if the database were carefully selected to be relevant to me or to the upcoming championship match, in most cases I really just want to get the general picture. The fact that black’s bishops are 34.1% and 35.4%, fine, maybe those are precise numbers, but I’d be just as happy with 34% and 35% or maybe even “around 33%”.
By the way, I see a wagering opportunity here. Actually a whole new bookmaking opportunity for Vegas. In game 1, how long will black’s c pawn last? I’ll take the under on 7 moves.
Re 3: nope, kings are never captured since a move that would lead to a position where the king could be captured is illegal. Furthermore, even checkmates occur rarely (at least in master level games) since most games are resigned long before checkmate. You could count resignation as the death of the losing player’s king, but that would be inconsistent with how survival of other pieces is defined. (I suppose there was no analysis of how the game have would have continued after resignation, thus when White resigns the game because he would lose his queen next move, this counts as a survival of the White queen here.)
Juho:
Yes, I was counting resignation or checkmate as the capture of a king. I agree that such a measure would not be perfect but I think it would be much more informative than just putting down “100.0%.”
If anyone is truly confused by the kings’ showing up as 100%, they probably have no use knowing about chess piece survival probabilities anyways….
Rahul:
It’s not about being confused, it’s about me wanting to see more information. When I criticize a graph, I’m not concern-trolling about the confusion of hypothetical uninformed audiences; rather, I’m generally expressing my own desire to see comparisons of interest more directly.
Since white wins 52-56% of the time [http://en.wikipedia.org/wiki/First-move_advantage_in_chess], you could reasonably use that as the white king survival range, and 44-48% for the black king. Or take out the draws, when both kings survive.
Nope. There are some draws as well.
Sorry, glanced over your last sentence.
In some sense, the difference between the champion & the next guy isn’t huge. So who wins might be influenced by relatively small factors. Perhaps being the champion is mentally stressful whereas as challenger you feel less burden? I’m speculating, of course.
My criticism is that the percentages are mapped only onto warm colors — the large difference between and knight and a bishop could be made much more apparent with a broader color palette that separates the numbers more. But it’s still an interesting and fun graph.
Is it really “often easier to win a rematch than to defend a championship”?
I have really no idea, but the difference might be that a sitting champion has his style studied by everyone while he cannot be as well versed in the styles of all those who are likely to challenge him. Then, for the rematch, this information asymmetry is leveled. This, of course, would work the best with a slow turn on top and a short span between the time the challenger is determined and the match itself.
Naive question: Does the fact that high level games sometimes finish early due to one player resigning mean that these data should be viewed as censored data? e.g. A particular pawn is more likely to be taken in the end game had it been played for longer? And if so, would this actually matter for the purposes of this analysis?
I was thinking about this too. At some point this question becomes really weird, because after a player has realized their loss is guaranteed, how can we say what move they would have made? All moves are equally bad at that point.
Alex:
One approach is to take a random sample of games that ended with resignations and then have an expert (or a computer) impute how the games would have gone had they been played until checkmate.
Do it with the computer. Stockfish for example.
For more chess trivia here’s another application of computers to human chess that I blogged recently:
http://models.street-artists.org/2014/09/05/randomized-chess/
The fact that computers are now definitely the best chess players should be used to human advantage IMHO.
If the audience is mostly experts it won’t matter perhaps? Most decent players won’t belabor a lost position through a endgame resulting in a forgone conclusion.
Have you seen the animated version? Its compiled from 2.2 million games, showing survival rate after each move. It takes a minute to load so be patient:
http://imgur.com/c1AhDU3
Neat! It’d also be interesting to see which are the dangerous spots of the board as the game progresses.
Hi, Mike!
The animation’s nice but what’s the deal with games ending? If a game ends after 20 moves, does that go into the stats for survival on move 21, with all the pieces left when a game ended after 20 moves surviving forever? Or do all pieces die when a game ends?
It’d be great to see the animation for each piece the probability of it being captured at a given position at each particular time. And I guess we could have something like overall survival rate.
Andrew should have his visualization class work on this one. It’s a great example.
Hey Bob! I’m not sure. I’m guessing that a game ending in 20 moves does not affect the 21-move stats. But the author did not write it up in detail. He is user TungstenAlpha on Reddit in the DataIsBeautful section if anyone wants to ask.
BTW – here is a version with King Piece Survival: http://imgur.com/llSA80R
And if anyone (Andrew’s class?) wants the original data it is the MillionBase set. See left column here: http://www.top-5000.nl/pgn.htm
I’ve recently been thinking about the boundaries of the board as a parameter that could be adjusted. 10×10 or 12×12 would still be manageable physically but would give some interesting variations. I’d suggest 10×10 should have 4 knights, and 12×12 should have 4 knights and 4 bishops, or 6 knights and 2 bishops… depending on your view on the church ;-)
Hey, what’s wrong with thick black hipster glasses? Of course, no hipster would put that much contrast in their print or web designs in 2014. Just look at how low key Yosemite is compared to earlier Mac OSes (there’s even a “high contrast” option if you want your lines back) and how light the newer IOS 8 is compared to earlier versions.
I can’t understand the “often” part of the title. It happens yes but often implies a phenomenon apart from ability. That is, if we limit games to very close competitors, then I’d expect a relatively random set of outcomes – meaning some ratio of draws to outright wins. In this case, motivation from losing and the focus it provides might matter, though it should be hard to tell if we’re limiting this to close competitors.
In one sense, I’m reminded of 2 of my cats. They’re brothers and fought every day of their lives (because they trusted each other so completely they could fight without injury risk). They were equally matched, one stronger, the other quicker, but neither by a lot given this was play-fighting not to the death. And they’d work on their moves. I’d see one win a few in a row and the other would come up with a new move (really, an old move used in a different spot because it’s fighting and the possible moves are limited, as they are in chess). The surprised loser would bolt and they’d go at it again, each trying for that bit of advantage. So I’d say you can “surprise” in a rematch because people, like cats, aren’t infinitely flexible in their responses and decisions so you can try something that’s not expected and get away with that in a particular match – and then have it happen to you next time. I’m not sure I’d say “rematch” is the right word; there should be switching of some sort among equals trying different things in a continuing series of “games” or “fights”.
The same happens in football and other sports: the other team has all your tendencies learned and the players are coached about what to expect. If you win consistently when both teams play according to their tendencies, you are likely just the superior team. If you are in a competitive match, which in some sports – like football – doesn’t necessarily mean equal talent, changing tendencies is important. You show this look and do something different out of it. Same thing happens in chess or in cat fights.
Defend may not be singular.
Have there been enough chess world championships with the same opponents so “often” has any meaning?
If we broaden this to include, say, all sporting events it’s pretty clear that one side can dominate the other for a long time.
For example, consider the Little Brown Jug (the annual Michigan and Minnesota football rivalry). Since 1968, Minnesota has won four times (including winning in 2014).
Here’s the data on chess championships, assembled by Spektrowski. The discussion mostly focused on age.
http://www.chess.com/blog/Spektrowski/average-age-and-age-differences-of-world-championship-matches
Counting the following as rematches, I end up with 6 cases in which the previous player won the rematch, and 6 cases in which a different player won. There are different ways to count the multiple rematches of Karpov and Kasparov, and the data set is small, show I’m showing my work below:
year lower alpha higher alpha winner who won rematch? Same or different than previous winner?
1934 Alexander Alekhine Efim Bogoljubov Alexander Alekhine same
1937 Alexander Alekhine Max Euwe Alexander Alekhine different
1985 Anatoly Karpov Garry Kasparov Anatoly Karpov same
1986 Anatoly Karpov Garry Kasparov Garry Kasparov different
1987 Anatoly Karpov Garry Kasparov Garry Kasparov same
1990 Anatoly Karpov Garry Kasparov Garry Kasparov same
1981 Anatoly Karpov Viktor Korchnoi Anatoly Karpov same
1969 Boris Spassky Tigran Petrosian Boris Spassky different
1896 Emanuel Lasker Wilhelm Steinitz Emanuel Lasker same
1961 Mikhail Botvinnik Mikhail Tal Mikhail Botvinnik different
1957 Mikhail Botvinnik Vasily Smyslov Vasily Smyslov different
1958 Mikhail Botvinnik Vasily Smyslov Mikhail Botvinnik different
Either I’ve not learned to format replies, or the formatting abilities are terrible.
In the post above, I show the year of the rematch, the two opponents (sorted in alpha order just so I could easily identify rematches), the winner, and whether the winner was the same or different than the previous winner.