God is in every leaf of every tree. The leaf in question today is the height of journalist and Twitter aficionado Jon Lee Anderson, a man who got some attention a couple years ago after disparaging some dude for having too high a tweets-to-followers ratio. Anderson called the other guy a “little twerp” which made me wonder if he (Anderson) suffered from “tall person syndrome,” that problem that some people of above-average height have, that they think they’re more important than other people because they literally look down on them.
After I raised this issue, a blog commenter named Gary posted an estimate of Anderson’s height using information available on the internet:
Based on this picture: http://farm3.static.flickr.com/2235/1640569735_05337bb974.jpg he appears to be fairly tall. But the perspective makes it hard to judge.
Based on this picture: http://www.catalinagarcia.com/cata/Libraries/BLOG_Images/Cata_w_Jon_Lee_Anderson.sflb.ashx he appears to be about 9-10 inches taller than Catalina Garcia.
But how tall is Catalina Garcia? Not that tall – she’s shorter than the high-wire artist Phillipe Petit http://www.catalinagarcia.com/cata/Libraries/BLOG_Images/Cata_w_Philippe_Petite.sflb.ashx. And he doesn’t appear to be that tall… about the same height as Claire Danes: http://cdn.theatermania.com/photo-gallery/Petit_Danes_Daldry_2421_4700.jpg – who according to Google is 5′ 6″.
So if Jon Lee Anderson is 10″ taller than Catalina Garcia, who is 2″ shorter than Philippe Petit, who is the same height as Claire Danes, then he is 6′ 2″ tall.
I have no idea who Catalina Garcia is, but she makes a decent ruler.
I happened to run across that comment the other day (when searching the blog for Tom Scocca) and it inspired me to put out a call for the above analysis to be implemented in Stan. A couple of other faithful commenters (Andrew Whalen and Daniel Lakeland) did this. But I wasn’t quite satisfied with either of those efforts (sorry, I’m picky, what can I say? You must’ve known this going in). So I just did it myself.
Modeling
Before getting to my model, let me emphasize that nothing fancy is going on. I’m pretty much just translating Gary’s above comment into statistical notation.
Here’s my Stan program:
transformed data {
real mu_men;
real mu_women;
real sigma_men;
real sigma_women;
mu_men <- 69.1;
mu_women <- 63.7;
sigma_men <- 2.9;
sigma_women <- 2.7;
}
parameters {
real Jon;
real Catalina;
real Phillipe;
real Claire;
real Jon_shoe_1;
real Catalina_shoe_1;
real Catalina_shoe_2;
real Phillipe_shoe_1;
real Phillipe_shoe_2;
real Claire_shoe_1;
}
model {
Jon ~ normal(mu_men,sigma_men);
Catalina ~ normal(mu_women,sigma_women);
Phillipe ~ normal(mu_men,sigma_men);
Claire ~ normal(66,1);
(Jon + Jon_shoe_1) - (Catalina + Catalina_shoe_1) ~ normal(9.5,1.5);
(Catalina + Catalina_shoe_2) - (Phillipe + Phillipe_shoe_1) ~ normal(2,1);
(Phillipe + Phillipe_shoe_2) - (Claire + Claire_shoe_1) ~ normal(0,1);
Jon_shoe_1 ~ beta(2,2);
Catalina_shoe_1 / 4 ~ beta(2,2);
Catalina_shoe_2 / 4 ~ beta(2,2);
Phillipe_shoe_1 ~ beta(2,2);
Phillipe_shoe_2 ~ beta(2,2);
Claire_shoe_1 / 4 ~ beta(2,2);
}
Hey! Html ate some of my code! I didn’t notice till a commenter pointed this out. In the declarations, the “shoe” variables should be bounded: “angle bracket lower=0,upper=1 angle bracket” for the men’s shoes, and “angle bracket lower=0,upper=4 angle bracket” for the women’s shoes.
I’ll present the results in a moment, but first here’s a quick discussion of some of the choices that went into the model:
– I got the population distributions of heights of men and women from a 1992 article in the journal Risk Analysis, “Bivariate distributions for height and weight of men and women in the United States,” by J. Brainard and D. E. Burmaster, which is the reference that Deb Nolan and I used for the heights distribution in our book on Teaching Statistics.
– I assumed that men’s shoe heights were between 0 and 1 inches, and that women’s shoe heights were between 0 and 4 inches, in all cases using a beta(2,2) distribution to model the distribution. This is a hack in so many ways (for one thing, nobody in these pictures is barefoot so 0 isn’t the right lower bound; for another, some men do wear elevator shoes and boots with pretty high heels) but, as always, ya gotta start somewhere.
– I took the height comparisons as stated in Gary’s comment, giving a standard deviation of 1 inch for each, except that I gave a standard deviation of 1.5 inches for the “9 or 10 inches” comparison between Jon and Claire, since that seemed like a tougher call.
– Based on the statement that Claire was 66 inches tall, I gave her a prior of 66 with a standard deviation of 1.
Inference
I saved the stan program as “heights.stan” and ran it from R:
heights <- stan_run("heights.stan", chains=4, iter=1000)
print(heights)
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
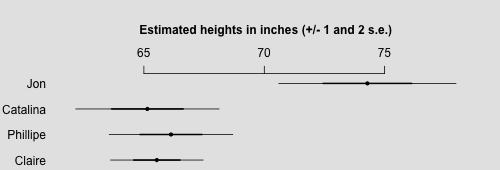
Jon 74.3 0.1 1.8 70.6 73.1 74.3 75.5 77.9 877 1
Catalina 65.1 0.1 1.5 62.3 64.1 65.1 66.2 67.9 754 1
Phillipe 66.1 0.0 1.3 63.7 65.2 66.1 67.0 68.6 813 1
Claire 65.5 0.0 1.0 63.8 64.9 65.5 66.1 67.5 1162 1
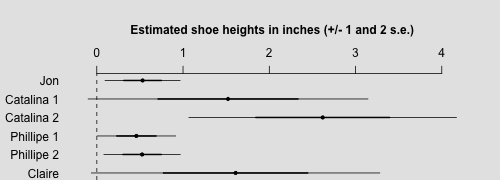
Jon_shoe_1 0.5 0.0 0.2 0.1 0.4 0.5 0.7 0.9 1658 1
Catalina_shoe_1 1.5 0.0 0.8 0.2 0.9 1.4 2.1 3.3 1708 1
Catalina_shoe_2 2.6 0.0 0.8 0.9 2.1 2.7 3.2 3.8 1707 1
Phillipe_shoe_1 0.5 0.0 0.2 0.1 0.3 0.5 0.6 0.9 1391 1
Phillipe_shoe_2 0.5 0.0 0.2 0.1 0.4 0.5 0.7 0.9 1562 1
Claire_shoe_1 1.6 0.0 0.8 0.2 1.0 1.5 2.2 3.3 1390 1
lp__ -21.6 0.1 2.5 -27.6 -23.1 -21.2 -19.8 -17.8 749 1
OK, everything seems to have converged, and it looks like Jon is somewhere between 6'1" and 6'4".
Tables are ugly. Let's make some graphs:
sims <- extract(heights,permuted=FALSE)
mon <- monitor(sims,warmup=0)
library("arm")
png("heights1.png", height=170, width=500)
par(bg="gray90")
subset <- 1:4
coefplot(rev(mon[subset,"mean"]), rev(mon[subset,"sd"]), varnames=rev(dimnames(mon)[[1]][subset]), main="Estimated heights in inches (+/- 1 and 2 s.e.)\n", cex.main=1, cex.var=1, mar=c(0,4,5.1,2))
dev.off()
png("heights2.png", height=180, width=500)
par(bg="gray90")
subset <- 5:10
coefplot(rev(mon[subset,"mean"]), rev(mon[subset,"sd"]), varnames=rev(c("Jon", "Catalina 1", "Catalina 2", "Phillipe 1", "Phillipe 2", "Claire")), main="Estimated shoe heights in inches (+/- 1 and 2 s.e.)\n", cex.main=1, cex.var=1, mar=c(0,4,5.1,2))
dev.off()
That is:
Model criticism
OK, now let's do some model criticism. What's in this graph that we don't believe, that doesn't make sense?
- Most obviously, some of the intervals for shoe height go negative. But that's actually not our model, it's coming from our crude summary of inference as +/- 2 sd. If instead we used the simulated quantiles directly, this problem would not arise.
- Catalina's shoes are estimated to be taller in her second picture (the one with Phillipe) than in the first, with Jon. But that's not so unreasonable, given the pictures. If anything, perhaps the intervals overlap too much. But that is just telling us that we might have additional information from the photos that is not captured in our model.
- The inferences for everyone's heights seem pretty weak. Is it really possible that Phillipe Petit could be 5'9" tall (as is implied by the upper bound of his 95% posterior interval)? Maybe not. Again, this implies that we have additional prior information that could be incorporated into the model to make better predictions.
Fitting a model, making inferences, evaluating these inferences to see if we have additional information we could include: That's what it's all about.
Software criticism
Finally, let's do the same thing with our code. What went wrong during the above process:
- First off, my Stan model wasn't compiling. It was producing an error at some weird place in the middle of the program. I couldn't figure out what was going on. Then, at some point in cutting and pasting, I realized what had happened: my text editor was using a font in which lower-case-l and the number 1 were indistinguishable. And I'd accidentally switched one for the other. I changed the font and fixed the problem.
- Again Stan gave an error, this time even more mysterious:
Error in compileCode(f, code, language = language, verbose = verbose) :
Compilation ERROR, function(s)/method(s) not created!Agreeing to the Xcode/iOS license requires admin privileges, please re-run as root via sudo. In addition: Warning message:
running command ‘/Library/Frameworks/R.framework/Resources/bin/R CMD SHLIB file3d6829c6b35e.cpp 2> file3d6829c6b35e.cpp.err.txt' had status 1
I posted the problem on stan-users and Daniel Lee replied that Apple had automatically updated Xcode and I needed to do a few clicks on my computer to activate the permissions.
- Then it ran, indeed, it ran on the first try, believe it or not!
- There were some issues with the R code. The calls to coefplot are a bit ugly, I had to do a bit of fiddling to get everything to look OK. It would be better to be able to do this directly from rstan, or at least to be able to make these plots with a bit less effort.
- Umm, that's about it. Actually the programming wasn't too bad.
Summary
I like Bayesian (Jaynesian) data analysis. You lay out your model step by step, and when the inferences don't seem right (either because of being in the wrong place, or being too strong, or too weak), you can go back and figure out what went wrong, or what information is available that you could throw into the model.
P.S. to Andrew Whalen and Daniel Lakeland: Don't worry, you've still earned your Stan T-shirts. Just email me with your size, and your shirts will be in the mail.
Naive question probably, but why is only Jon’s shoe a beta(1,1) & the rest all shoes beta(2,2)?
That was a mistake (one could call it a bug in the sense that it was the result of my sloppy programming style). I just went back and fixed it.
Thanks! It might be a silly example but it helps seeing how you approach such a problem and write the code and hear about the problems you encounter.
I had no idea you could put a general expression on the left hand side of a sampling statement
eg: (Jon + Jon_shoe_1) – (Catalina + Catalina_shoe_1) ~ normal(9.5,1.5);
For all the hoo-ha about priors, you got pretty much the same inference that I did even though we used fairly different priors for the shoe heights.
I didn’t post my model code + output because I was afraid the blog would eat it with all the < signs and indentation and soforth. If you can figure out how to get it plopped into a comment properly I will make some further points.
The lack of preview on comments is pretty lousy. When will wordpress fix that?? ;-)
Also this morning on pretty much every comment I’ve posted I get something about how my comment “timed out” even if it only takes me a few seconds to write one line.
Dan:
I think you can put in code using the “pre” tag.
I tried the “code” tag below, and that didn’t work very well (lost all the indentation, but didn’t suck the life out of it due to < at least) also I put the table in using the pre tag, but that lost all its formatting as well… I have never been able to figure out how to do this in comments, when writing the blog entries you get previews and soforth and can debug… oh well at least the code and data are there. I’ll revisit after lunch.
Yes, you can put general expressions on the left side of a sampling statement, but it’s your job to account for any Jacobian adjustments they induce from non-linear transforms of parameters. In general in Stan, a sampling statement like
is just shorthand for incrementing the log probability with foo_log, the log probability function (density or mass) for foo,
with one key difference: the sampling statement form drops constant terms (we’re planning to give users control over dropping constants in both sampling and functional forms in a future version, but we won’t change the default behaviors).
WordPress hasn’t fixed lack of preview in 10 years, so I wouldn’t hold my breath.
I visit another blog (Scott Aaronson’s Shtetl Optimized), and that seems to use WordPress & has a neat preview feature. Not sure how they manage it….
http://www.scottaaronson.com/blog/?p=2011#comments
So just to be as explicit as possible about what “it’s your job to account for any Jacobian adjustments they induce from non-linear transforms of parameters” entails:
funky_func(y) ~ foo(theta);
// and now I need account for the log-Jacobian of funky via
increment_log_prob(loggy_J(y));
That about right?
(My pre-tags, where did they go? I am doing something wrong.)
Let’s be even more explicit. because I think this is confusing. I haven’t thought too carefully about what Stan is doing on the inside, but it’s worth checking that I understand it.
Stan works with log(p(data | params) * p(params) * C) where C is some constant related both to 1/p(data) and possibly normalizing factors left out of the calculation of some of the p(params) etc. It works internally with the logarithms, but I’ll keep that explicit here
a statement
funky_func(y) ~ foo(theta);
where y,theta are parameters enters into the p(params) portion, since it doesn’t have anything to do with the data. Stan does:
increment_log_prob(foo(F(y),theta))
But, Stan needs to calculate log(p(y)), not log(p(F)) which in this case is log(p(F) dF/dy) *provided that funky_func is 1-1*
so we need to do
increment_log_prob(log_dF_dy(y))
The whole thing is easier to understand if you explicitly make everything dimensionless by choosing an infinitesimal dy:
p(y) dy = p(F)dF = foo(F(y),theta) dF
p(y) = foo(F(y),theta) dF/dy
log(p(y)) = log(foo(F(y),theta) + log(dF/dY)
I also like the exposition of using general formulae on the left hand side of the sampling statement.
I think the stan manual has a few examples of this, but andrews post made heavy use of it. It was a refreshing reminder.
Ok, trying out my code:
modstr <- " transformed data { real usmaleheightcm; real usmaleheightsdcm; real usfemheightcm; real usfemheightsdcm; real clairdaneshcmwiki; real cmperinch; cmperinch <- 2.54; usmaleheightcm <-175; usmaleheightsdcm <- 10; usfemheightcm <- 160; usfemheightsdcm <- 6; clairdaneshcmwiki <- (5*12+6)*cmperinch; } parameters{ real jonleeandersh; real catgarch; real phillipph; real clairdanesh; real catgarcheelsjla; real catgarcheelsphp; real clairdanesheels; real jla_boost_abv_avg; } model{ clairdanesheels ~ exponential(1/(2*cmperinch)); catgarcheelsjla ~ exponential(1/(2*cmperinch)); catgarcheelsphp ~ exponential(1/(2*cmperinch)); clairdanesh ~ normal(clairdaneshcmwiki,1*cmperinch); phillipph ~ normal(clairdanesh+clairdanesheels,1*cmperinch); catgarch ~ normal(usfemheightcm,usfemheightsdcm); catgarch ~ normal(phillipph-catgarcheelsphp-3*cmperinch,2*cmperinch); jla_boost_abv_avg ~ exponential(1/(usmaleheightsdcm*3.0/2)); jonleeandersh ~ normal(usmaleheightcm+jla_boost_abv_avg,usmaleheightsdcm); jonleeandersh ~ normal(catgarch + catgarcheelsjla + 9*cmperinch,2*cmperinch); } " samps <- stan(model_code=modstr,chains=2,iter=2000);And the output:
Inference for Stan model: modstr. 2 chains, each with iter=2000; warmup=1000; thin=1; post-warmup draws per chain=1000, total post-warmup draws=2000. mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat jonleeandersh 186.7 0.3 7.1 174.4 181.7 186.3 191.3 201.7 738 1 catgarch 159.7 0.2 4.6 150.8 156.6 159.6 162.7 169.2 725 1 phillipph 171.6 0.2 4.5 163.3 168.6 171.4 174.3 181.8 451 1 clairdanesh 167.5 0.1 2.5 162.3 165.9 167.5 169.1 172.5 813 1 catgarcheelsjla 4.6 0.2 4.5 0.1 1.4 3.3 6.3 16.4 660 1 catgarcheelsphp 4.3 0.1 3.7 0.1 1.5 3.2 6.2 13.9 691 1 clairdanesheels 4.2 0.2 3.6 0.1 1.4 3.3 6.0 13.4 433 1 jla_boost_abv_avg 10.9 0.3 8.2 0.4 4.6 9.3 15.5 31.1 756 1 lp__ 19.7 0.1 2.2 14.5 18.5 20.0 21.4 22.9 540 1Hopefully it doesn’t look terrible.
Nope :-) well at least it’s not destroyed by the less than signs, but the indentation and table formatting is awful.
I switched in the “pre” code and it looks better now.
Ah yes, that looks a LOT better. I don’t understand exactly, because I used the “pre” tag for the table and the “code” tag for the code, and my table didn’t look anything like your table… wordpress is all goofy about this stuff.
Heights are in centimeters, divide by 2.54 for inches. so that puts jonlee height at about 73.5 inches (expected value, or 6 ft 1.5 in), with 95% interval [68.7,79.4] or 5ft 9 to 6ft 7 a pretty wide range.
When modelling is there an easy way to encode our differential relative trust in various information? e.g. High trust in the US heights distribution but lower in, say, “Jon is 9-10 inches taller than Catalina Garcia”
Yes. It’s just priors and measurement error models all the way up.
Can you describe how, say in this example.
Say, I trust the prior “Jon ~ normal(mu_men,sigma_men);” 100 times more than I trust the information that “(Jon + Jon_shoe_1) – (Catalina + Catalina_shoe_1) ~ normal(9.5,1.5);”
Is “100 times more” too vague? Any better way to state this?
what’s a range that you are “almost absolutely sure” that (Jon + Jon_shoe_1) – (Catalina + Catalina_shoe_1) falls into? Let’s say you’re willing to say you’re almost absolutely sure that it’s between say 3 inches and 15 inches… then make it
~ normal(9,2)
Don’t like that, maybe you think it might be between 0 inches and 20 inches? make it ~normal(10,3) or maybe ~normal(10,4)
At some point, if you make it wide enough you’ve got to believe that it’s in that range… ~normal(9,20) I guarantee for sure it’s in the “high probability region” (defined as mean plus or minus 2 or 3 or 4 standard deviations) of that prior.
I guess, you can implement your idea directly by making it a 2 component model with 0.01 probability on “(Jon + Jon_shoe_1) – (Catalina + Catalina_shoe_1) ~ normal(9.5,1.5);” and 0.99 probability on some default, but 1) it seems to be unnecessarily complicated and 2) I’ve no idea how Stan programs multi-component distribution. Heck, you can even make your 1:100 believe ratio a fitting parameter.
Very nice analysis. I had a couple of errors running your code as-is, though. I thought others might find this useful.
In the R code:
I’m guessing that “stan_run” is a custom function that you’ve created? I just replaced that with “stan”
In the stan code:
I had to put bounds to all the “*_shoe*” variables, otherwise I would get a series of
Error in function stan::prob::beta_log(N4stan5agrad3varE): Random variable is -0.317581:0, but must be >= 0!Rejecting proposed initial value with zero density.
Error in function stan::prob::beta_log(N4stan5agrad3varE): Random variable is 1.13518:0, but must be less than or equal to 1Rejecting proposed initial value with zero density.
followed by
Initialization failed after 100 attempts. Try specifying initial values, reducing ranges of constrained values, or reparameterizing the model.
error occurred during calling the sampler; sampling not done
I still got a couple of those errors after setting the lower bounds, and some warnings of Metropolis proposals being rejected, but at the end it worked and I got pretty much the same results.
Perhaps the dev version of stan has all sorts of improvements compared to 2.4.0, so that’s why Andrew didn’t get these problems?
Damn html ate my angle brackets! The bounds were in the code, they just disappeared when I put them into the blog post.
Does the beta distribution not automatically constrain them?
I’d love to know what die hard Frequentists make of all this.
The distributions clearly aren’t frequency distributions, at least not accurately so, and the thing they are distributions of aren’t “random draws” from a population. Yet at the end of the day Bayesians are estimating an objective fact (Anderson’s height, to within the usual tolerances).
The choice of distributions clearly isn’t arbitrary. General knowledge of shoes such as “people don’t casually wear three feet tall shoes because they’d fall over all the time” are being used and aren’t easily dismissed as “subjective opinions”.
So which of the Frequentists gambits would they use to discount this? Would they go with the “this is secretly frequentist” gambit? If so, how would they pull that off?
I’m not die-hard anything, but had the same question. Here’s a start on an answer;
Presumably one could imagine a sampling distribution of pictures of John Lee A and Catalina G that we might observe, in a search for pictures of the guy, of which this is only one. Same goes for all the other pairings, presumably conditional on searching for pictures of Catalina. With n of 1 sampled from all these distributions, one would have to use other information to make assumptions about them, e.g. that the observations may reflect heights wearing plausibly-sized heels, that sometimes people slouch, whatever. This is okay; frequentist does not mean assumption-free, or even assumption-lite.
Putting it all together, you could presumably come up with an interval that, under valid assumptions, would cover the true height of John Lee A in a given percentage of replicate experiments of this sort – which one could assess for sensitivity to the assumptions, if desired.
It also struck me the estimation process is very like network meta-analysis, which can be motivated from a Bayesian point of view but also without Bayes.
oooh, the old “this problem was randomly chosen from a population of problems” gambit. Interesting.
I think any “gambit” is elsewhere; the problem is pretty well-specified – just estimate John Lee A’s height. For most of the data (i.e. pictures obtained by typing the appropriate minor celebrity’s name into Google Images) random sampling from the essentially-infinite population of digitized pictures of them seems like an okay data-generation model, albeit not perfect.
Exactly how that data relates to John Lee A’s height is a tricky measurement error/missing data problem, but should be possible.
How would you fit it into frequentism? I agree it’s an interesting challenge.
Like you say it’s fairly well defined. To first approx there is an unknown underlying parameter, what’s his face’s height. A frequentist is presumably interested in the reliability of the procedure of estimating height based on google image searches. Raising and tackling this question seems as worthwhile as formalizing back of the envelope calculations.
> like network meta-analysis, which can be motivated from a Bayesian point of view but also without Bayes.
In network meta-analysis, there is information completely missing on a total treatment group, so not sure it can be addressed without an informative prior for that group which would make it Bayes. Yes, very common for folks to construct a phantom likelihood (or mean and se) for that missing group, but that violates Andrew’s rule below
(a) Each piece of information comes into the posterior distribution exactly once.
New datapoint: http://prodavinci.com/sistema/wp-content/uploads/2012/01/Anderson.jpg (Jon vs former Iranian president Mahmoud Ahmadinejad, height 1.68m ~ 66inch).
Excellent.
Anderson appears to be more than half a foot taller.
Andrew: “Fitting a model, making inferences, evaluating these inferences to see if we have additional information we could include: That’s what it’s all about.”
I’d like to push you here a little to put your finger on exactly the value added, and what we learn from, the modeling exercise. (I’m not coming at this as an skeptic, which I am not, but as genuinely curious.) Here are two possible interpretations:
1. We are having the model tell us what we already know. That is, we have an idea in our head of what would be reasonable inferences, and we are tweaking the model to get it to spit that image out. I suspect we would have gotten pretty close if we simply skipped Stan and everything and had simply drawn the final graph by hand. Writing down a model is just a way of rationalizing in a public fashion how we came to our conclusion.
2. We are having the model tell us something we already know but in the process learn something new. I think here is the real value added of course. The question is why we learn something new. Put differently, where did our brains fail? For example, I had not though of the same person wearing different shoes on different occasions. But this is an instance, what I am interested in are general classes of failures. For example:
– Processing capacity: A computer may be better at integrating tons of information (but humans play chess pretty well, and do many complex tasks easily that computers find impossible);
– Errors and omissions: A program, like algebra, can highlight errors and omissions in internal logic (but this seems somewhat serendipitous);
– Biases and heuristics: E.g. availability biases and other things that may be less powerful when dealing with code as opposed to direct guessing (but these biases may filter into the prior);
Any thoughts?
PS In game theory, for example, a common assumptions is that agents update their beliefs using Bayes’ theorem. If so, if you show them the various pictures they should get the same guess as they would if they used Stan. This is a useful assumption, but it is hard to believe.
depends on the definition of “already know”. If you define it loosely enough, given a prior, likelihood and data, we “already know” the posterior.
But, particularly when we’re dealing with higher dimensionality and missing data, it’s not trivial to make the inference by eyeball. And then when we start contrasting differences between parameters, it can get even trickier to eyeball parameter differences in a consistent way. A posterior on the difference in parameters makes the comparisons explicit.
now that i think about it, almost all the time I set up a bayesian estimation model, it’s ultimately in service of performing contrasts…
Fernando:
You ask what is gained by the above exercise. To start with, nobody (except maybe Jon Lee Anderson) cares much about Jon Lee Anderson’s height: it is a demonstration problem intended to illustrate methods.
The first thing it’s illustrating is Bayesian measurement error models. These are not widely understood, but if you do it carefully it’s surprisingly easy to just add error terms to express different aspects of bias and variance in measurement.
The second thing is it’s illustrating the use of Stan. Again, it’s (to me) impressively easy to implement the model straight in Stan in one take. Sure, this particular example could be done in other ways. But, to be honest, those other ways aren’t so easy, they involve various shortcuts and worries about how the data are being included. Once you’ve put in the overhead to learn Bayes and Stan (which you might have done, for example, to fit nonlinear hierarchical models), it’s pretty effortless to solve measurement-error problems too.
An analogy might be the use of a pocket calculator to solve a simple problem such as 5*(38-12)+46. Easy enough to do by hand, but if you have the calculator (which of course is the product of millions of dollars of R&D involving semiconductors, etc.) you might as well use it. Stan is the “calculator” here.
The third thing (and I don’t think I got this point across very well in my post) is to illustrate Bayesian (Jaynesian) data analysis: the method that works by laying out very clear assumptions, working out their implications, and then adding additional information as necessary if the conclusions don’t make sense.
Finally, just about any worked example—this one included—reveals some little things that can be useful. For example, the problem I had with the “pre” tag and the brackets in my Stan code, the feature that you can include arbitrary expressions on the left side of a squiggle sign in a Stan model, the use of the scaled beta as a quick prior for the shoe heights, the use of coefplot() to display the inferences.
Andrew:
I think I was not sufficiently clear. I completely understand why you are doing this, and so on. Moreover, I am not criticising this particular application. I think it is a great example!
But I was also trying to use this toy example to ask a broader question related to the style of inference you propose. You touch on it again when you state: “adding additional information as necessary if the conclusions don’t make sense”. Do we already know the conclusion? If so, why bother?
One answer might be that we add more information to get rid of nonsense like negative heel height say. That comes from the prior not the conclusion.
But at times it seems as if we know what the conclusion should look like, and are just iterating through the modeling to get there. Put bluntly, is like we are beating a confession out of the model rather than learning from it.
That may be ok when we want to describe data (we want y_rep to look like y) but in cases like this, where we are trying to solve a mystery as it where, it seems the approach can lead one astray. I don’t think its happening here but I just think that the approach is still very heuristic.
PS I am not saying that is bad. It can be very useful. But it also suggests it can be improved and formalized more, I think.
Fernando:
I agree. This process can and should be formalized more. One reason for me to do little examples step by step is to build the intuition that can lead for formalizing. I’m not so old, I still have visions of progress! In particular, one issue is that there’s uncertainty. If a result “doesn’t make sense,” this implies a conflict with other information that might be included in the model, but at some point these “don’t make sense” claims are only probabilistic.
> I’m not so old, I still have visions of progress!
So did Peirce when he was not old ;-)
http://en.wikipedia.org/wiki/Charles_Sanders_Peirce#Theory_of_categories
First, there is the thought of writing a generative model, how was Jon’s and other’s heights determined and how were the observations we got generated, both in terms of probabilistic representations.
Second, given a probabilistic representation, as Fernando put it “given a prior, likelihood and data, we “already know” the posterior” so we have essentially error free access to that and with that we note _Brute facts_ are somewhat different.
Third, we interpret the above “makes sense” judgmentally deciding how it could be made less wrong or perhaps hold steady with it for now (at least until more serious _Brute facts_ come to our attention).
I find the “Bayesian (Jaynesian) data analysis” as you put it so colourfully direct and straightforward in at least the first two steps.
I think what I am trying to get at – especially in the context of measurement model – is the notion of experimenter’s regress http://en.m.wikipedia.org/wiki/Experimenter's_regress
How about some more pictures in which John Lee Anderson is standing next to somebody so we can get more data?
John Lee Anderson is several inches taller than his brother Scott:
http://sangam.org/2011/02/images/JonLeeAnersonandScottAndersonin1988.jpg
Here he’s bending weigh down to shake the hand of movie star Gael Garcia Bernal, whom Google.com says is 5’6″.
http://www.zimbio.com/photos/Jon+Lee+Anderson
Here’s he with Hugo Chavez, whom Google says was 5-8, but they’re not side by side, so the picture isn’t too useful:
http://www.theclinic.cl/2013/07/03/jon-lee-anderson-periodista-y-escritor-queria-vivir-como-un-hombre-salvaje/
Here, even seated, Anderson towers over film maker Saul Landau, who is of unknown height:
http://www.zimbio.com/photos/Jauretsi+Saizarbitoria/Jon+Lee+Anderson
Here, slumped in a chair, he appears to be much taller than random female students:
http://www.frontlineclub.com/capturing-the-story-with-jon-lee-anderson/
Here Anderson towers over a man whose face has been blurred out presumably because he’s some kind of desperado:
http://www.antoniosalas.org/terrorismo/articulo/antonio-salas-palestinian-carlos-jackal-was-my-friend
Here Anderson is standing in a line up on stage of prize winners with the president of Columbia U., Lee Bollinger (Anderson looks a couple of inches taller than Bollinger, whom Professor Gelman has likely met):
http://cabotprize.com/the-2013-cabot-prizes-ceremony/
Here is Anderson with Latin American intellectuals and Canadian writer John Ralston Saul. Anderson and Saul are similar in height, and looking at pictures of Saul with other people, he is clearly a six-footer at least.
http://grupopenta.com.co/1589/hay-festival-cartagena-de-indias-2013/
In general, Anderson appears to be the among the tallest people in most pictures he is in, although he tends to get his photograph taken a lot with Latin Americans and Middle Easterners rather than Dutchmen and Serbs. He has the body language of a man of considerable height.
Here’s benchmark Lee Bollinger with NYC’s giant new mayor Bill De Blasio, who is said to be 6-8 and might be taller.
http://earth.columbia.edu/articles/view/3138
Here’s Bollinger with Bill Gates, whom Google calls 5’10”.
http://engineering.columbia.edu/web/newsletterarchive/fall05/billgates.php
Bollinger appears an inch or inch and a half taller than Gates.
Is the Hispanic height distribution significantly different than the American? Is it ok to assume that Catalina Garcia is Hispanic?
Instead of normal(5’3″,2″) another mean maybe?
Wonder if that’d change any estimates substantially?
Because Mr. Anderson is considerably taller than average, but was given the average man’s prior, his height is made smaller in the posterior. This is all good, regression to the mean and so forth. But for everybody else it means that their height is pulled upward. If there were lots of comparisons, it would not matter. Everyone else would be added a little extra, but because this “recoil” is shared by only 3 people, it might be noticeable. Suggested cure: you’ve got interested in Mr. Anderson’s height because you suspected it to be unusual. Make a prior for him wider or even flat.
In my model (above) I used the information originally given about Anderson at a book signing (that he looked taller than various random people who were probably average sized) to bump the mean value of his prior distribution up by 3/2 of a standard deviation (vs the overall male population). My model didn’t use shoe heights for males though (I figured women wearing “flats” were about as much taller than barefoot as men wearing typical loafers or whatever).
I disagree that we should make Anderson’s height flatter, the point is, if we have some general information that he seems “taller” than average, then make his prior height have an average which is taller than the average for men in general, don’t make it flatter… because that would imply implausible heights, such as say 7 or 8 ft tall.
To be more specific, I created a parameter jla_boost_above_avg and made it exponentially distributed with mean value 3/2 of a standard deviation (of the whole population of men in the US).
Of course, if you do have some specific information like from book signing event, it is reasonable to include it. But I would be hesitant to do it just on a hunch that he is tall because he calls others “little twerp”. Anyways, data always wins against speculation.
Definitely a book signing photo is different information than just a comment about “little twerp” so the information in your prior *should* be different for the two cases.
Not so much that your prior should be different. More that you start with the same prior but then the book signing photo is information that gets included as data.
Well, in my model, the jla_boost_above_avg is a parameter, and I put a prior over it that was informed by the book signing photo. so, it’s data-based but it doesn’t enter into what you’d call the “likelihood”.
The prior and likelihood breakdown is a little bit artificial I suppose.
Yes, the key principles are:
(a) Each piece of information comes into the posterior distribution exactly once.
(b) To the extent the inferences don’t make sense, this is an indication that there is additional prior information not included in the model.
John Lee Anderson is notably taller than his brother Scott Anderson, another writer.
I like how my reasoning naturally runs in circles: JLA is a lot taller than SA, so that raises the probability that JLA is tall, but if JLA is tall then SA probably isn’t short (they are, after all, brothers), which adds credence to JLA being tall.
Steve:
Them being brothers can be included in the statistical analysis (and in the Stan model) via a correlation.
In this example, of course, all these data are overkill, but I can well imagine similar reasoning being used to good effect in sparse-data settings such as data from an archeological site (or, for that matter, tree-ring reconstruction, which is an area I have worked on where uncertainties are huge).
I like these simple examples such as estimating heights or ranking soccer teams or spell checking because, if you think about them carefully, it is possible to gain general insights and see some general statistical principles in a setting where the prior information is easy to grasp.
In general, is there a hard constraint on how many parameters versus how many model equations one uses? Like in linear algebraic sets of equations? Just wondering.
Can one under / over constrain the model?
Rahul:
If we have informative priors there are no real constraints, I think.
Andrew:
If I may pick your brain more, what advantage did we get my modelling it this way than just a set of point inequalities. i.e.
That’d give you approximately the same point estimates for all their heights? OK, we lost the intervals but those are kinda too wide anyways to be of much help.
And adding in the prior about population heights doesn’t seem to have helped enhance accuracy by much in this particular case?
Rahul:
See here. The short answer is that it can be helpful to understand a method in the context of a simple example.
I agree. No other example helped me understand Stan as well as this post! So, thanks! :)
Shouldn’t the Catalina-Philippe line be the other way around? He’s taller in that photo, right? Or am I misunderstanding how the code works?
Another toy problem: http://www.r-bloggers.com/tiny-data-approximate-bayesian-computation-and-the-socks-of-karl-broman