We have no fireworks-related posts for July 4th but at least we have an item that’s appropriate for the summer weather. It comes from Daniel Lakeland, who writes:
Recently in one of your blog posts (“priors I don’t believe”) there was a discussion in which I was advocating the use of dimensional analysis and dimensionless groups to normalize every model, including statistical regression models. People wanted an example that made sense in social sciences, but since I don’t really have any social science examples to hand, I couldn’t provide one. However, I do have an interesting example problem that I just blogged, although it’s a physics problem, perhaps it illustrates the techniques well enough that one of your readers could run with it on a social sciences problem, or alternatively perhaps one of your readers would be interested in collaborating with me to develop a social science example.
Lakeland’s post starts with:
I’ve been working on my front-crawl swim stroke as an effort to improve my fitness.
But it doesn’t take too long to get to this:
and this:
So you should enjoy it. This indeed is the sort of analysis we don’t see enough of in statistics, I think.
P.S. Regarding priors, I wanted also to feature this comment from Chris on that earlier post:
This non-technical description of Bayes’ rule bugged me: “Final opinion on headline = (initial gut feeling) * (study support for headline)”. I think I’d have written something like “educated guess” rather than “gut feeling”. Not all gut feelings are of equal merit. One can have gut feelings about technical matters where they have some experience and are reasonably well informed. (I’d call that an educated guess.) Conversely, one can have gut feelings re matters where they are thoroughly uninformed.
I agree. One problem with the whole “subjective Bayes” slogan is the elevation of subjectivity into a principle, which is all too close to an anything-goes view which is contrary to many of the goals of science.
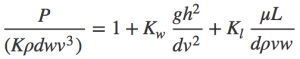
PS: this post was written up by Andrew and placed in the delay queue a while back. Since then I also did a follow up post:
http://models.street-artists.org/2014/05/20/more-swimming-dragpower-thoughts/
which uses a slightly different normalization factor for power that better illustrates the tradeoff between piston drag and wave drag.
Thanks! Does anyone here know of any application of dimensionless analysis in the Social Sciences?
Googling “dimensional analysis social sciences” gives this paper:
Use of dimensional analysis in social science research
James E. Bruno,
Osher Doctorow,
Christhart H. Kappner
Socio-Economic Planning Sciences, Volume 15, Issue 3, 1981, Pages 95–99
http://www.sciencedirect.com/science/article/pii/0038012181900240
The abstract looks interesting; it doesn’t seem like a PDF is available.
Dimensional analysis is wonderful. People interested in this might like this short book:
Scaling, by G. I. Barenblatt, Cambridge Univ. Press, Cambridge, 2003
It includes such wonders as why the speed of a rowboat varies as the number of oarsmen to the 1/9 power, and G. I. Taylor’s brilliant determination of the energy of an atomic bomb blast based on the combination of Life magazine photos and dimensional analysis. (I put the latter into a brief introduction to dimensional analysis I wrote: http://physics-server.uoregon.edu/~raghu/TeachingFiles/Fall07Phys351/Dimensional%20Analysis%20Lecture%20Notes.pdf )
I was thinking about that this morning. As an illustration of the kind of thing one might consider doing in a model of public opinion, suppose you’re interested in how opinions about economic policy vary. One could hypothesize that location (as a proxy for culture), age, and wealth might matter. Wealth and age are of course related to some degree.
You could hypothesize that to a first approximation, that for economic opinion, what matters is not your absolute age, but your age relative to the time it would take your social group to accumulate some significant amount of wealth.
Rescaling age in years A by income divided by the local cost of some large and important good (such as a house) might reveal a symmetry of opinion across regions and SES classes:
Instead of opinion O being a function of Age, Wealth, and Location, O = f(A,W,L) you might start with something like
O = g((I-E)/H (A-A_v),L)
where I is income, E is some measure of “core expenses”, H is the price of a house, A is age in years, and A_v is voting age (18 years in US) which also tends to be close to when people start earning money.
Using this assumption of symmetry on an appropriately defined scale, we’ve eliminated one dimension from our function g (it depends only on two quantities instead of three).
Note that (I-E)/H (A-A_v) is a dimensionless group and it’s value for most people is going to be O(1), for example someone with an income of $50,000 who lives in a region where “minimum” expenses are say $30,000 in a region where a typical house is $300,000 would at age 60 have a value for this measure of age of 2.8, whereas a 30 year old would have 0.8 on this scale.
I thought so.
> have some experience
I that is an important distinction and came out in Andrew’s comment once that a prior can be just crappy data analysis of past experience.
Crappy data analysis of past experience can be acceptable while no possible analysis of non-experience would ever prove acceptable (e.g. non-informative priors)
FYI since I didnt see it mentioned, there was recently an article plus discussions published in Technometrics in 2013 on this topic which (focused on design of expirements).