Amy Cohen writes:
A surgeon showed me the “report card” his hospital received about his surgical group. The figure below shows what the report card looks like. I am very curious to hear what you think about the “deciles of the odds ratio” approach to evaluate and rank hospitals used by the American College of Surgeons.
I replied: I don’t know enough about the substantive context to say too much here. But, speaking generally, I am skeptical of those very high values for some of those odds ratios. I suspect that much of what is plotted in this graph is just noise. But I respect the goals underlying the plot, and I like that it displays a lot of information efficiently.
And then she wrote:
My concern with the decile approach to identifying opportunities for improvement is that it violates a principle of quality improvement: chasing noise is fruitless or worse, because it leads to tampering with a system in a way that can make it worse. In the paper, the authors admit that the 95% CIs don’t yield many signals, so they added highest decile of the ORs as signals, too. In other words, they superimposed a ranking system that encourages the hospitals to chase the noise!
That’s not good.
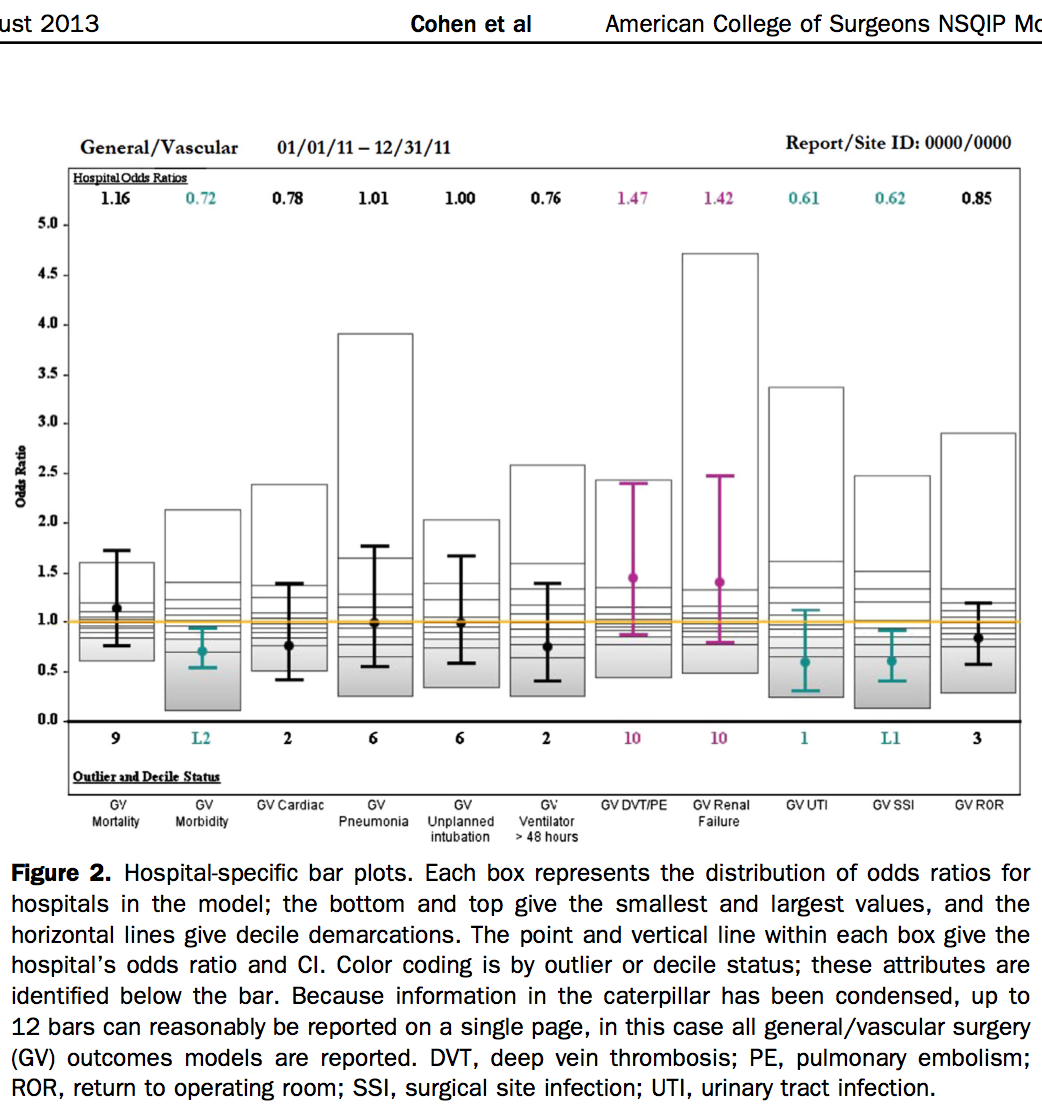
In addition I would note odds ratios need to be plotted on logarithmic scale. The poor ratios below one are shrunk to nothing.
Instead of making a ratio appear like an absolute measure why not just compute an absolute measure (e.g. the risk difference)?
That seems fine – although I’m sure you can construct situations in which the odds ratio is informative (e.g. think absolute risk difference between [0.03 – 0.01 = 0.02] and relative risk [0.03/0.01=3]).
Note the motivation for showing the bars is to display uncertainty in the estimates. The same would have to be true for showing an absolute change in risk. If you want to stray away from discrete intervals, you might choose something like the posterior simulations that Gelman and Hill show in their multi-level book and display a series of histograms.
I also commend wanting to show confidence intervals, my experience in industry “performance metrics” they are just point estimates of change (and often come with a % change attached). Inevitably what happens there is chasing the noise, as the series with the largest percent changes often have the largest variance.
Plotting on a log scale and making clear (either through education, labels or other graphical changes) that wider bars means more uncertainty as opposed to larger estimates would IMO make this a more reasonable graph.
Without knowing what these odds ratios represent, the decile system is interesting, in that it gives another measure of the spread, but is not substantively different from the confidence intervals. This is really just the same information plotted twice. Also, for the model to spit out ORs in the 3-5 range seems very unlikely.
Plus ca change… we have the same issue here in the UK. Having collected the data (with noble intentions), people hate to admit that there’s nothing exciting to see. So they go looking for ‘outliers’, which ends up just being a list of the top 10. This initiative is an interesting, if painstakingly slow, antidote to it though.
In general, I think this is a pretty terrible graph. Maybe I’m just slow, but it took me quite some time to understand exactly what I was looking at. First off, people have been really trained to look at bar charts. At first glance, that’s exactly what this looks like. But that’s not what the bars represent. What we really want to look at are the dots and lines, but the bars overwhelm my eyes.
As far as the odds-ratios go, even as a trained statistician, I find odds-ratios to be counter-intuitive, and always have to stop and think about what they really represent before diving into the data. I’m guessing that many others have to do the same. So, I hate OR as a general way to convey information to the public – especially in a report card format. I haven’t spoken with many surgeons, but of the other doctors that I have always spoken with, they tend to cringe when I mention that I am a statistician. How many surgeons can even explain what an odds-ratio means?
The decile ranges are interesting, but I’m not sure they add that much value. Why not just state what decile the hospital lands in and call it a day?
I would be that the best predictor of a hospital being at the very top OR very bottom of the distribution of odds-ratios is how few surgeries they did. The fewer N within hospital, the noisier the odds ratios, the higher the probability of being in the tail.
I’d put $1.50 against your dollar, if anyone is up for some stats gambling.
No bet! The caption tells us we’re looking at individual hospitals, with all data, with no mention of any scaling or sampling, and the differences in narrowness of the CIs tell us that the hospitals vary a great deal in size.
My particular taste would be to use violins rather than boxes for the distributions (assuming they are calculated in a way that accounts for sampling error). Also, I would prefer to scale the y-axis by the log, but I recognize that that may cause some readers difficulty as not everyone is comfortable with non-linear axes. Additionally, the single number summaries reported on the bottom should also have intervals associated with them since the estimate precision is not very good.
Pingback: Briefly | Stats Chat
i don’t exactly understand the objections, cause i don’t exactly understand what the report card authors were trying to convey.
one piece of missing info is the instructions that came with the report card.
without those instructions, we really can’t say if this is a good or bad graph (except for the color blind, and the small print on the axes, and the lack of raw data, and the failure to note if this is corrected for patient status at entry (eg, the hosp that is willing to do surgery on sick old folks – do they get praise, or dinged ?)
Pingback: Odds Ratios NEED To Be Graphed On Log Scales | Andrew Wheeler
How about a bilinear scale, if reading log graphs is difficult for the intended audience?
I.e., same distance between 3:1 and 1:1 as between 2:1 and 1:2 (and between 1:1 and 1:3.