Yesterday we were looking at the musical taste proximity between European countries. But what about the proximity between European nations in terms of the genes? The field of population genetics investigates this problem. I have taken some Y chromosome data, and computed the distance between two nations based on their genetic distance.

The result, obtained with MDS is as follows:

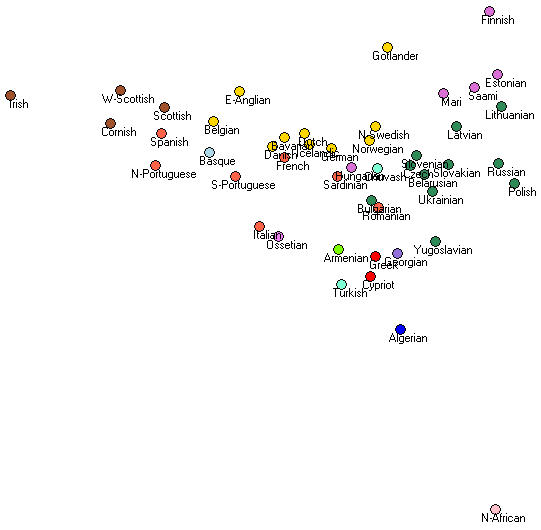
I’ve color-coded different language groups. We can see that North Africans are quite different, and that within Europe, there is a clear gradient from the East to West, with several clusters. The islands of Gotland and Sardinia are composed of a diverse mix from different populations.

The interesting point, however, is that I’ve initialized the positions of points to the geographic positions, which can roughly be interpreted as a prior. This is a bit unusual: usually the points are randomly initialized, or initialized with some sort of a linear dimension reduction technique, such as with Torgerson’s procedure.

Multidimensional scaling is that old way of embedding a set of points described in terms of their similarities into a lower-dimensional space so that the Euclidean distances in this space reflect the similarities. While there are closed-form solutions to the problem when the transformation is linear, usually based on the SVD, one can achieve lower stress by allowing nonlinear transformations such as SMACOF.

SMACOF is a deterministic hill-climb, but it depends on the starting point. The starting point can either be considered to be a nuisance, but it can also be considered to be the equivalent of a regularization term or a prior. Csiszár, for example, pointed out that iterative scaling finds the point from the set of solutions that satisfy constraints that is closest to the starting point. While this doesn’t exactly fit the regularization term or prior setting, it is nevertheless a very appropriate way of stabilizing MDS: with so many co-dependent parameters, a MDS posterior distribution seems incomprehensible (although Fig 3 in Jackman’s Multidimensional Analysis of Roll Call Data via Bayesian Simulation does provide an interesting visualization, but with the use of informative priors). In this sense, SMACOF and iterative scaling can be seen as the updating of the prior.

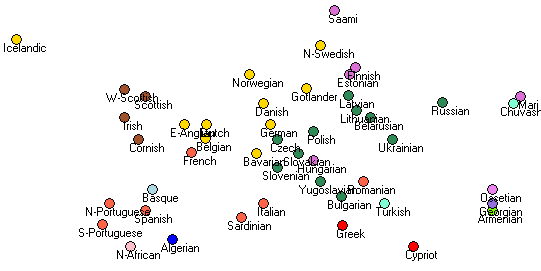
This is the original placement:

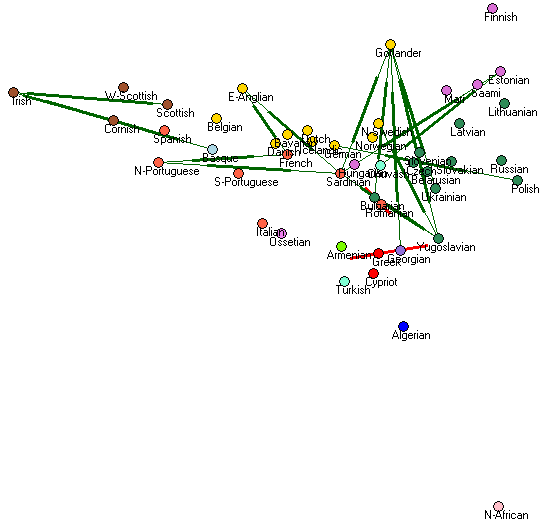
Two dimensions are insufficient to show the complexity of the data. Here you can see the stresses (green means too far, red is too close):

Finally, this is what comes out from initializing the points randomly:

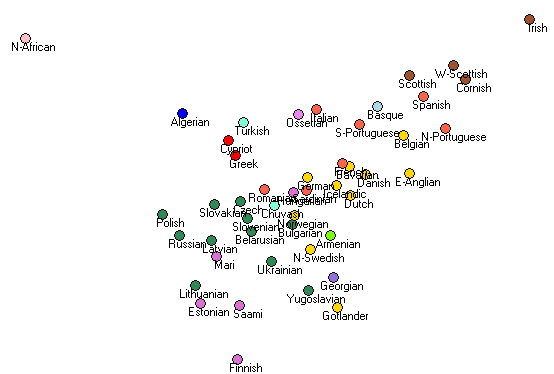
Definitely not as easy to understand as the geographic original – yet it has better “stress” than the prior-based one. The sensible geographic prior nicely helps orient the result.

In summary, the benefit of priors goes beyond the Bayesian methodology.